No CrossRef data available.
Article contents
Truncated Jacobi triple product series II: Li, Lin, and Wang’s nonnegativity conjecture
Part of:
Additive number theory; partitions
Basic hypergeometric functions
Combinatorics
Discontinuous groups and automorphic forms
Published online by Cambridge University Press: 19 June 2025
Abstract
The investigation of truncated theta series was popularized by Andrews and Merca. In this article, we establish an explicit expression with nonnegative coefficients for the bivariate truncated Jacobi triple product series: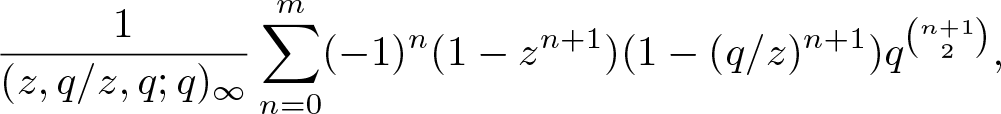
\begin{equation*}\frac{1}{(z,q/z,q;q)_\infty}\sum_{n=0}^{m}(-1)^n(1-z^{n+1})(1-(q/z)^{n+1})q^{\binom{n+1}{2}},\end{equation*}
which can be regarded as a companion to Wang and Yee’s truncation of the triple product identity. As applications, our result confirms a conjecture of Li, Lin, and Wang and implies a family of linear inequalities for a bi-parametric partition function. We also work on another truncated triple product series arising from the work of Xia, Yee, and Zhao and derive similar nonnegativity results and linear inequalities.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
Footnotes
‡
This article originally published with errors. Those errors have now been corrected and the article updated. A correction notice has also been published.
References
Andrews, G. E.. q-Series: Their development and application in analysis, number theory, combinatorics, physics, and computer algebra (American Mathematical Society, Providence, RI, 1986).Google Scholar
Andrews, G. E.. Bailey chains and generalized Lambert series. I. Four identities of Ramanujan. Illinois J. Math. 36 (1992), 251–274.CrossRefGoogle Scholar
Andrews, G. E.. The theory of partitions (Cambridge University Press, Cambridge, 1998).Google Scholar
Andrews, G. E. and Merca, M.. The truncated pentagonal number theorem. J. Combin. Theory Ser. A 119 (2012), 1639–1643.CrossRefGoogle Scholar
Andrews, G. E. and Merca, M.. Truncated theta series and a problem of Guo and Zeng. J. Combin. Theory Ser. A 154 (2018), 610–619.CrossRefGoogle Scholar
Berkovich, A. and Garvan, F. G.. Some observations on Dyson’s new symmetries of partitions. J. Combin. Theory Ser. A 100 (2002), 61–93.CrossRefGoogle Scholar
Corteel, S. and Lovejoy, J.. Overpartitions. Trans. Amer. Math. Soc. 356 (2004), 1623–1635.CrossRefGoogle Scholar
Fine, N. J.. Basic hypergeometric series and applications (American Mathematical Society, Providence, RI, 1988).CrossRefGoogle Scholar
Gasper, G. and Rahman, M.. Basic hypergeometric series. 2nd edn (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Guo, V. J. W. and Zeng, J.. Two truncated identities of Gauss. J. Combin. Theory Ser. A 120 (2013), 700–707.CrossRefGoogle Scholar
Li, X., Lin, B. L. S. and Wang, A. Y. Z.. Strong truncated Jacobi triple product series. Submitted.Google Scholar
Mao, R.. Proofs of two conjectures on truncated series. J. Combin. Theory Ser. A 130 (2015), 15–25.CrossRefGoogle Scholar
Wang, C. and Yee, A. J.. Truncated Jacobi triple product series. J. Combin. Theory Ser. A 166 (2019), 382–392.CrossRefGoogle Scholar
Xia, E. X. W., Yee, A. J. and Zhao, X.. New truncated theorems for three classical theta function identities. European J. Combin. 101 (2022), 23.CrossRefGoogle Scholar
Yee, A. J.. A truncated Jacobi triple product theorem. J. Combin. Theory Ser. A 130 (2015), 1–14.CrossRefGoogle Scholar
A correction has been issued for this article:
Linked content
Please note a has been issued for this article.