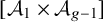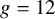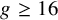1 Introduction
1.1 Moduli of abelian varieties
Given an abelian variety X of dimension g and an ample line bundle L, there is a polarization
$$ \begin{align*} \theta_L : X \longrightarrow &\ X^\vee \\ x \ \ \mapsto &\ t_x^*L \otimes L^{-1} \end{align*} $$
with kernel of the form
$$ \begin{align*}\ker (\theta_L) = (\mathbb{Z}/d_1 \times \ldots \times \mathbb{Z}/d_g)^2 \end{align*} $$
for a unique list of positive integers
$\delta = (d_1, \ldots , d_g)$
satisfying
$d_i \mid d_{i+1}$
so that
$\left (\prod d_i\right )^2 = \deg (\theta _L)$
. The list
$\delta $
is the polarization type. For fixed g and
$\delta $
, the collection of all such polarized abelian varieties
$$ \begin{align*} \mathcal A_{g, \delta} = \left\lbrace \begin{array}{c} (X,\theta) : X\text{ is an abelian variety of dimension }g\\ \text{ and }\theta:X \longrightarrow X^\vee\text{ is a polarization of type }\delta \end{array}\right\rbrace \end{align*} $$
has the structure of a smooth Deligne–Mumford stack of dimension
$\binom {g+1}{ 2}$
, see [Reference Mumford31]. We refer to [Reference Chai and Faltings12] and [Reference Birkenhake and Lange5] for foundational aspects of these spaces.
Over the complex numbers, we can identify
$\mathcal A_{g,\delta }$
with the stack quotient of the Siegel upper half space
$\mathcal H_g$
by an arithmetic subgroup of the symplectic group
$\operatorname {Sp}(2g, \mathbb {Q})$
. As a moduli stack of abelian schemes, there exists a universal polarized abelian scheme with a zero section:
The pullback under s of the relative sheaf of differentials
$\Omega _\pi $
is the Hodge bundle, which we denote by
${\mathbb E}_{g, \delta }$
, or by
${\mathbb E}_g$
. Alternatively,
${\mathbb E}_g = \pi _*\Omega _\pi $
.
The polarization
$\theta $
is principal if
$\delta =(1,\ldots ,1)$
; we say that
$\theta $
is a principal polarization. The moduli space of principally polarized abelian varieties
$\mathcal A_g$
will be our main focus, but the moduli spaces of higher degree polarizations will play an important role.
1.2 Noether-Lefschetz loci in
$\mathcal A_g$
The Néron-Severi group of an abelian variety is a free abelian group, whose rank is the Picard number of X. A general point in
$\mathcal A_{g,\delta }$
has Picard number
$1$
, and the locus where the Picard number is at least
$2$
is known as the Noether-Lefschetz locus. The Noether-Lefschetz locus is a countable union of closed and reduced subvarieties of
$\mathcal A_{g,\delta }$
, whose general element is either
-
• an abelian variety with a nontrivial abelian subvariety, or
-
• an abelian variety with real multiplication.
see [Reference Debarre and Laszlo18]. We will focus on the first case.
Given an integer
$u \leq g/2$
and a polarization type
$\delta = (d_1, \ldots , d_u)$
we consider the Noether-Lefschetz subvarieties of
$\mathcal A_g$
$$ \begin{align*}\operatorname{NL}_{g,\delta} = \left \lbrace (A, \theta) \in \mathcal A_g \left| \begin{array}{c} A\text{ has an abelian subvariety }B \\ \text{and }\theta|_{ B}\text{ is of type }\delta \end{array}\right.\right\rbrace. \end{align*} $$
An abelian variety is simple if it does not have any nontrivial abelian subvariety.
If
$\delta = (d)$
(so
$u=1$
), we will use the notation
$\operatorname {NL}_{g,d}$
instead.
We show in Section 2.2 that these are the irreducible components of the Noether-Lefschetz locus given by nonsimple abelian varieties. For example, if
$\delta = (\underbrace {1,\ldots ,1}_{u\text { times}})$
then
$\operatorname {NL}_{g, \delta }$
is the image of the natural product map
$$ \begin{align} \mathcal A_u \times \mathcal A_{g-u} \longrightarrow\mathcal A_g. \end{align} $$
More generally, the locus
$\operatorname {NL}_{g,\delta }$
will be the image of a twisted product map, as we will explain in Section 2.2.
1.3 The tautological rings
The Chern classes of the Hodge bundle
$$ \begin{align*}\lambda_i = c_i({\mathbb E}_{g,\delta}) \end{align*} $$
generate the Chow ring of
$\mathcal A_{g,\delta }$
for
$g \leq 3$
and
$\delta = (1,\ldots , 1)$
(see [Reference van der Geer37]). In general, the subring
$$ \begin{align*}\mathsf{R}^*(\mathcal A_{g,\delta}) : = \operatorname{im} \left(\mathbb{Q}[\lambda_1, \ldots , \lambda_g] \longrightarrow \mathsf{CH}^*(\mathcal A_{g,\delta})\right) \end{align*} $$
generated by the
$\lambda _i$
will be a strict subset of the Chow ring called the tautological ring of
$\mathcal A_{g,\delta }$
. The following result follows from [Reference van der Geer38, Theorem 3]:
Theorem 1. Let
$\delta =(d_1, \ldots , d_g)$
be a polarization type. Then
$$ \begin{align*}\mathsf{R}^*(\mathcal A_{g,\delta}) = \frac{\mathbb{Q}[\lambda_1, \ldots , \lambda_g]}{\langle c({\mathbb E}_{g,\delta})c({\mathbb E}_{g,\delta}^\vee)-1, \, \lambda_g \rangle}. \end{align*} $$
The proof appears in Section 2.1. The tautological ring is in fact isomorphic to the cohomology ring of the Grassmannian of Lagrangian hyperplanes in a vector space of dimension
$2(g-1)$
, and therefore it is Gorenstein with socle of degree
$\binom {g}{ 2}$
and independent of
$\delta $
, see [Reference van der Geer38].
1.4 The action of the Hecke algebra
In [Reference Canning, Oprea and Pandharipande15], it was proven that the class
$[\mathcal A_1 \times \mathcal A_{5}]\in \mathsf {CH}^5(\mathcal A_6)$
is not tautological. Their method consists of computing the pullback of
$[\mathcal A_1 \times \mathcal A_{5}]$
under the Torelli morphism
$$ \begin{align*}\operatorname{Tor} : \mathcal M_{g}^{ct} \longrightarrow \mathcal A_g, \end{align*} $$
that sends a curve to the group of multidegree
$0$
line bundles on it, where
$\mathcal M_{g}^{ct}$
is the moduli space of stable curves of compact type. Then, they use the completeness of Pixton’s relations [Reference Pandharipande, Pixton and Zvonkine35] on
$\overline {\mathcal M}_{6}$
, proven by Canning, Schmitt, and Larson [Reference Canning, Larson and Schmitt13] and computer computations to check that
$\operatorname {Tor}^*([\mathcal A_1 \times \mathcal A_{5}])$
does not agree with the pullback of its tautological projection (1.3), which we define in the next section. We extend their results using a different strategy, which we explain now.
For each
$n \geq 1$
, consider the stack
$$ \begin{align*}\mathcal B_{g,n} = \left\lbrace f: (X,\theta_X) \longrightarrow(Y, \theta_Y) \left| \begin{array}{c} (X, \theta_X), (Y, \theta_Y) \in \mathcal A_g, f\text{ is a} \\ \text{homomorphism, and }f^*\theta_Y = n\theta_X \end{array}\right.\right\rbrace\!. \end{align*} $$
There is a correspondence
where the morphisms are just the forgetful maps. By pullback from the left and pushforward to the right, they give rise to Hecke operators
$T_n : \mathsf {CH}^{g-1}(\mathcal A_g) \longrightarrow \mathsf {CH}^{g-1}(\mathcal A_g)$
. In Section 4 we show that the Hecke operators preserve tautological classes but shift the polarization type of the
$\operatorname {NL}_{g,d}$
. The pullback of
$\operatorname {NL}_{g, 2}$
under the Torelli morphism, restricted to the locus of smooth curves
$$ \begin{align} \operatorname{Tor} : \mathcal M_{g} \longrightarrow \mathcal A_g \end{align} $$
is the bielliptic locusFootnote
1
, which is shown to be nontautological for
$g =12$
in [Reference van Zelm39], and
$g \geq 16$
even in [Reference Arena, Canning, Clader, Haburcak, Li, Chi Mok and Tamborini2]. This proves the following:
Theorem 2. For
$g=12$
and
$g \geq 16$
even, we have that
$[\mathcal A_1 \times \mathcal A_{g-1}]\not \in \mathsf {R}^{g-1}(\mathcal A_g)$
.
Note that we only need to work on the moduli space of smooth curves, where the pullback under Torelli is easier to compute.
1.5 The tautological projection
Canning, Molcho, Oprea, and Pandharipande have constructed in [Reference Canning, Molcho, Oprea and Pandharipande14] a way to associate to any cycle class a tautological class in a natural way, which we call its tautological projection. They calculate the tautological projection of product cycles
$[\mathcal A_{g_1} \times \ldots \times \mathcal A_{g_l}]$
. Finding formulas for the tautological projection of other natural families of cycles is an interesting question.
We explain their construction briefly. Let
$\overline {\mathcal A}_g$
be a smooth toroidal compactification of
$\mathcal A_g$
, as constructed in [Reference Ash, Mumford, Rapoport and Tai3], and define the
$\lambda _g$
-pairing on
$\mathcal A_g$
:
$$ \begin{align*}\mathsf{CH}^k(\mathcal A_g) \times \mathsf{CH}^{\binom{g}{2}-k}(\mathcal A_g) \longrightarrow \mathsf{CH}^{\binom{g}{2}}(\mathcal A_g) \longrightarrow \mathbb{Q} \end{align*} $$
by the formula
$(\alpha , \beta ) \mapsto \int _{\overline {\mathcal A}_g} \bar {\alpha }\cdot \bar {\beta }\lambda _g$
, where
$\bar {\alpha }$
and
$\bar {\beta }$
are extensions of the cycles
$\alpha $
and
$\beta $
. The pairing is well defined because
$$ \begin{align*}\lambda_g |_{\overline{\mathcal A}_g \smallsetminus \mathcal A_g} = 0, \end{align*} $$
see [Reference Canning, Molcho, Oprea and Pandharipande14, Theorem 3].
Unlike the case of curves, the restriction of the
$\lambda _g$
pairing to the tautological ring of
$\mathcal A_g$
is perfect; this was shown in [Reference van der Geer38].
Definition 1 [Reference Canning, Molcho, Oprea and Pandharipande14, Definition 4].
The tautological projection
$\operatorname {taut} : \mathsf {CH}^k(\mathcal A_g) \longrightarrow \mathsf {R}^k(\mathcal A_g)$
is the composition:
$$ \begin{align*}\mathsf{CH}^k(\mathcal A_g) \longrightarrow (\mathsf{CH}^{{\binom{g}{2}}-k} (\mathcal A_g))^\vee \longrightarrow (\mathsf{R}^{{\binom{g}{2}}-k}(\mathcal A_g))^\vee \stackrel{\cong}{\longrightarrow} \mathsf{R}^k(\mathcal A_g), \end{align*} $$
where the first and third arrows are given by the
$\lambda _g$
-pairing, and the second one is the dual to the inclusion.
Unraveling the definitions, we see that
$\operatorname {taut}(\alpha )$
is the unique tautological class such that
$$ \begin{align*}\int_{\overline{\mathcal A}_g} \alpha \cdot \Lambda \cdot \lambda_g = \int_{\overline{\mathcal A}_g} \operatorname{taut}(\alpha) \cdot \Lambda \cdot \lambda_g \end{align*} $$
for any tautological class
$\Lambda $
.
The tautological projections of the product cycles
$[\mathcal A_u \times \mathcal A_{g-u}]$
were calculated in [Reference Canning, Molcho, Oprea and Pandharipande14, Theorem 6]. For example,
$$ \begin{align} \operatorname{taut}([\mathcal A_1 \times \mathcal A_{g-1}]) &= \frac{g}{6|B_{2g}|} \lambda_{g-1}, \end{align} $$
$$ \begin{align} \operatorname{taut}([\mathcal A_2 \times \mathcal A_{g-2}]) &= \frac{g(g-1)}{360 |B_{2g}||B_{2g-2}|} \lambda_{g-1} \lambda_{g-3}, \end{align} $$
where
$B_i$
is the i-th Bernoulli number. In Section 3.1, we extend their result to the Noether-Lefschetz locus given by nonsimple abelian varieties:
Theorem 3. If
$\delta = (d_1, \ldots , d_u)$
is a polarization type and
$d = d_1 \cdot \ldots \cdot d_u$
then
$$ \begin{align*}\operatorname{taut}([\operatorname{NL}_{g,\delta}]) = c \cdot \operatorname{taut}([\mathcal A_u \times \mathcal A_{g-u}]), \end{align*} $$
where
$$ \begin{align*}c = d_1^{2u-2}d_2^{2u-6}\ldots d_u^{-2u+2}\prod_{1\leq i<j\leq u} \prod_{p \mid d_j/d_i}\frac{(1-p^{-2(j-i)})}{(1-p^{-2(j-i+1)})}d^{2(g-u)+1}\prod_{j=1}^u\prod_{p \mid d_j}(1-p^{-2(j +g-2u))}), \end{align*} $$
and the products are over primes.
In particular, we haveFootnote 2
$$ \begin{align*}\operatorname{taut}([\operatorname{NL}_{g,d}])=\frac{gd^{2g-1}}{6 |B_{2g}|} \cdot \prod_{p \mid d}(1-p^{2-2g}) \lambda_{g-1}, \end{align*} $$
and
$\operatorname {taut}([\operatorname {NL}_{g, (d_1, d_2)}])$
is
$$ \begin{align*}\left(\frac{g(g-1)d_1^{2g-1}d_2^{2g-5}}{360|B_{2g}||B_{2g-2}|} \prod_{p \mid d_1}(1-p^{6-2g}) \prod_{p \mid d_2}(1-p^{4-2g})\prod_{p \mid d_2/d_1}\frac{(1-p^{-2})}{(1-p^{-4})}\right)\lambda_{g-1}\lambda_{g-3}. \end{align*} $$
Greer and Lian [Reference Greer and Lian25, Reference Greer, Lian and Sweeting26] consider the stacks
$$ \begin{align*}\widetilde{\operatorname{NL}}_{g,d} = \left\lbrace f:E \longrightarrow(A,\theta)\left|\begin{array}{c}(A, \theta) \in \mathcal A_g, E\text{ is an elliptic curve and }\\f\text{ is a homomorphism such that }\deg(f^*\theta)=d\end{array}\right.\right\rbrace, \end{align*} $$
which have several connected components that correspond to our
$\operatorname {NL}_{g,e}$
for
$e \mid d$
. They conjecture that the pushforward to
$\mathcal A_g$
of their fundamental classes should be the Fourier coefficients of a modular form of weight
$2g$
. As a consequence of Theorem 3, we can partially verify the conjecture:
Corollary 4. Define
$[\widetilde {\operatorname {NL}}_{g,0}]$
as
$ \frac {(-1)^g}{24}\lambda _{g-1}$
. Under the change
$q=e^{2\pi i \tau }$
, we have that
$$ \begin{align*}\operatorname{taut}\left( \sum_{d \geq 0}[\widetilde{\operatorname{NL}}_{g,d}]\, q^d\right) = \frac{(-1)^g}{24}E_{2g}(\tau)\lambda_{g-1}, \end{align*} $$
where
$E_{2g}$
is the Eisenstein modular function, of weight
$2g$
.
In Section 4 we introduce the
$\mathbb Q$
-vector space
$\mathbf {NL}_g \subset \mathsf {CH}^{g-1}(\mathcal A_g)$
generated by the cycles
$[\widetilde {\operatorname {NL}}_{g,d}]$
for
$d \geq 0$
. A. Pixton has conjectured that
$\mathbf {NL}_g$
has the same dimension as the space
$\operatorname {Mod}_{2g}$
of modular forms of weight
$2g$
for the group
$\operatorname {SL}_2(\mathbb Z)$
. In light of Corollary 4, we propose the following strengthening of Pixton’s conjecture.
Conjecture 1. There exists a perfect pairing
$$ \begin{align*}\Phi : \operatorname{Mod}_{2g} \times \mathbf{NL}_g \longrightarrow \mathbb Q \end{align*} $$
such that, for any modular form f of weight
$2g$
,
$$ \begin{align*}\sum_{d \geq 0} \Phi(f, [\widetilde{\operatorname{NL}}_{g,d}]) q^d \end{align*} $$
is the Fourier expansion of f at
$i \infty $
, where
$q= e^{2\pi i \tau }$
.
By [Reference Borcherds6, Theorem 3.1.], this determines a precise collection of relations between the cycles
$[\widetilde {\operatorname {NL}}_{g,d}]$
. Conjecture 1 is similar in shape to several results about special cycles on orthogonal Shimura varieties in the Kudla-Millson program [Reference Bruinier8, Reference Bruinier9, Reference Bergeron, Li, Millson and Moeglin10]. To our knowledge, it is not clear that Conjecture 1 follows from these results.
Remark 5. In [Reference Greer, Lian and Sweeting26], the authors show that the images of the cycles
$\widetilde {\operatorname {NL}}_{g,d}$
under the map
$$ \begin{align*}\widetilde{\operatorname{NL}}_{g,d} \longrightarrow\mathcal A_1 \times\mathcal A_{g-1} \end{align*} $$
that remembers the domain and codomain of the homomorphism vanish in cohomology, but give nonzero modular forms after adding some level structure. This does not contradict our result, since
$\mathcal A_1$
is not proper.
1.6 The homomorphism property and Gromov-Witten theory of the universal elliptic curve
If
$\alpha $
is a tautological class, then for any
$\beta $
,
$$ \begin{align} \alpha \cdot\operatorname{taut}(\beta) = \operatorname{taut}(\alpha \cdot \beta). \end{align} $$
Indeed, if
$\Lambda $
is a tautological class,
$$ \begin{align*} \int_{\overline{\mathcal A}_g} \operatorname{taut}(\alpha \cdot \beta) \cdot \Lambda \cdot \lambda_g &= \int_{\overline{\mathcal A}_g} \beta\cdot \alpha \cdot \Lambda \cdot \lambda_g = \int_{\overline{\mathcal A}_g} \operatorname{taut}(\beta) \cdot \alpha \cdot \Lambda\cdot \lambda_g. \end{align*} $$
Definition 2. Let
$\alpha , \beta \in \mathsf {CH}^*(\mathcal A_g)$
. We say that the pair
$(\alpha , \beta )$
has the homomorphism property if
$$ \begin{align} \operatorname{taut}(\alpha \cdot \beta) = \operatorname{taut}(\alpha) \cdot \operatorname{taut}(\beta). \end{align} $$
We do not know if the tautological projection is a ring homomorphism in general, but we find that this is the case in several situations
Theorem 6. If
$\alpha , \beta \in \mathsf {CH}^*(\mathcal A_g)$
are cycles supported on the Noether-Lefschetz locus given by nonsimple abelian varieties, then both sides of equation (1.6) vanish, so
$(\alpha , \beta )$
has the homomorphism property.
The authors in [Reference Canning, Oprea and Pandharipande15] define extensions of the tautological ring of van der Geer that include Noether-Lefschetz cycles. For instance, they consider the ring
$\mathsf {R}^*_{\mathsf {pr}}(\mathcal A_g)$
generated by the pushforwards to
$\mathcal A_g$
of classes in
$$ \begin{align*}\mathcal A_{g_1} \times \ldots \times \mathcal A_{g_l} \end{align*} $$
that can be written in terms of the
$\lambda $
classes on each factor, or more generally the ring generated by all Noether-Lefschetz loci and the pushforwards of their tautological classes. Theorem 6 shows that the tautological projection
$$ \begin{align*}\operatorname{taut} : \mathsf{R}_{\mathsf{pr}}^*(\mathcal A_g) \longrightarrow \mathsf{R}^*(\mathcal A_g) \end{align*} $$
is a ring homomorphism.
Question 1. For which natural subrings of
$\mathsf {CH}^*(\mathcal A_g)$
is the tautological projection a ring homomorphism?
Faber and Pandharipande introduced in [Reference Faber and Pandharipande22] the
$\lambda _g$
-pairing on the moduli space of curves of compact type:
$$ \begin{align} \mathsf{CH}^k(\mathcal M_g^{ct}) \times \mathsf{CH}^{2g-3-k}(\mathcal M_g^{ct}) \longrightarrow \mathsf{CH}^{2g-3}(\mathcal M_g^{ct}) \longrightarrow \mathbb{Q}, \end{align} $$
given by
$(\alpha , \beta ) \mapsto \int _{\overline {\mathcal M}_g} \bar {\alpha }\cdot \bar {\beta }\lambda _g$
, where
$\lambda _g$
is the top Chern class of the Hodge bundle on
$\overline {\mathcal M}_g$
.
The Torelli morphism
$\operatorname {Tor} : \mathcal M_g^{ct} \longrightarrow \mathcal A_g $
is proper, and its image is the locus of Jacobians,
$\mathcal J_g$
.
We want to investigate the homomorphism property for the pair
$(\alpha , [\mathcal J_g])$
, where
$\alpha \in \mathsf {CH}^*(\mathcal A_g)$
. By [Reference Namikawa33], the Torelli morphism extends to a morphism between
$\overline {\mathcal M}_g$
and some toroidal compactification of
$\mathcal A_g$
while still preserving the Hodge bundle, and so
$(\alpha , [\mathcal J_g])$
has the homomorphism property if and only if
$\operatorname {Tor}^*(\alpha - \operatorname {taut}(\alpha ))$
pairs to
$0$
with any
$\lambda $
class in
$\mathcal M_g^{ct}$
. A more refined result is given in Proposition 20.
Consider the universal family of elliptic curves with a zero section:
The stack
$\overline {\mathcal M}_{g,1}(\pi ,d)$
is the moduli space of log-stable maps of degree d to the fibers of
$\pi $
from a pointed curve of genus g. It is a proper Deligne–Mumford stack, is equipped with maps
$$ \begin{align*}\mathsf{ev} : \overline{\mathcal M}_{g,1}(\pi,d) \longrightarrow \overline{\mathcal E}, \qquad \mathsf{ft} : \overline{\mathcal M}_{g,1}(\pi,d) \longrightarrow \overline{\mathcal M}_{g,1}, \end{align*} $$
and has virtual class of dimension
$2g$
. The cotangent line at the marking of the domain curve defines a line bundle on
$\overline {\mathcal M}_{g,1}(\pi ,d)$
, whose first Chern class is
$$ \begin{align*}\psi \in \mathsf{CH}^1(\overline{\mathcal M}_{g,1}(\pi,d)). \end{align*} $$
We consider Gromov-Witten invariants defined from this data:
$$ \begin{align*}\langle \tau_i(s)\Lambda \rangle_{g, d}^\pi := \int_{[\overline{\mathcal M}_{g,1}(\pi, d)]^{vir}}\psi^i \mathsf{ev}^*[s]\mathsf{ft}^*\Lambda, \end{align*} $$
where
$\Lambda \in \mathsf {CH}^*(\overline {\mathcal M}_{g,1})$
and
$i \geq 1$
.
If
$(C,p)$
is a marked curve of compact type, there is an Abel-Jacobi map
$C \longrightarrow \operatorname {Jac}(C)$
. If
$\operatorname {Jac}(C)$
has an elliptic subgroup, the composition of the Abel-Jacobi map and the dual of the inclusion of E gives rise to a morphism
$(C,p) \longrightarrow (E,0)$
and every morphism from C to an elliptic curve arises in this way. This suggests that
$\mathrm {Tor}_1^{-1}(\operatorname {NL}_{g,d})$
is connected with the Gromov-Witten invariants arising from
$\overline {\mathcal M}_{g,1}(\pi ,d)$
, where
$$ \begin{align*}\operatorname{Tor}_1 : \mathcal M_{g,1}^{ct} \longrightarrow \mathcal A_g \end{align*} $$
sends a pointed curve to its Jacobian. We will make this precise in Proposition 23, with an ingredient being the recent work of Greer and Lian (more concretely, [Reference Greer and Lian25, Theorem 2]) to identify
$\mathrm {Tor}_1^*([\operatorname {NL}_{g,d}])$
with the virtual class of a component of
$\mathsf {ft}^{-1}(\mathcal M_{g,1}^{ct})$
.
If
$([\operatorname {NL}_{g,d}], [\mathcal J_g])$
has the homomorphism property, we can replace
$$ \begin{align*}[\overline{\mathcal M}_{g,1}(\pi,d)]^{vir} \cdot \mathsf{ev}^*[q]\lambda_g \end{align*} $$
with
$\operatorname {Tor}_{1}^*(\operatorname {taut}([\widetilde {\operatorname {NL}}_{g,d}])) \lambda _g$
for integral evaluations, thus arriving at the following conjecture:
Conjecture 2. For all
$g \geq 2$
,
$d \geq 1$
, and
$\Lambda \in \mathsf {R}^*(\overline {\mathcal M}_g)$
is an insertion divisible by
$\lambda _g$
then
$$ \begin{align*}\langle \tau_i(s)\Lambda \rangle_{g, d}^\pi := \frac{g \sigma_{2g-1}(d)}{6|B_{2g}|} \int_{\overline{\mathcal M}_{g,1}} \psi^i\lambda_{g-1} \Lambda, \end{align*} $$
where
$B_{i}$
is the i-th Bernoulli number and
$\sigma _{k}(n) = \sum _{m \mid n} m^k$
.
A particular case is
$$ \begin{align} \langle \tau_1(s) \lambda_g \lambda_{g-2}\rangle_{g,d}^{\pi} = \frac{|B_{2g-2}|}{24(2g-2)!}\sigma_{2g-1}(d), \end{align} $$
by [Reference Faber and Pandharipande21, Theorem 4]. Notice that this formula has the same shape as the corresponding Gromov-Witten invariants of an elliptic curve, see [Reference Pixton34, Proposition 4.4.6]. The following result summarizes the connections:
Theorem 7. Let
$g \geq 2$
. The following are equivalent:
-
a) Formula (1.8) holds for all d.
-
b) Conjecture 2 holds.
-
c) For all d, the pair
$([\operatorname {NL}_{g,d}], [\mathcal J_g])$
has the homomorphism property. -
d) For all d,
pairs to
$$ \begin{align*}\operatorname{Tor}^*([\operatorname{NL}_{g,d}] - \operatorname{taut}([\operatorname{NL}_{g,d}])) \in \mathsf{CH}^{g-1}(\mathcal M_g^{ct}) \end{align*} $$
$0$
with any tautological class in
$\mathsf {R}^{g-2}(\mathcal M_g^{ct})$
under the
$\lambda _g$
pairing (1.7).
Remark 8. In a subsequent paper [Reference Lopez, Pandharipande and Tseng29] with Pandharipande and Tseng, we will show that formula (1.8) holds. This shows that all the statements in Theorem 7 hold. We will also explain the connections to the quantum cohomology of the Hilbert scheme of points in
$\mathbb {C}^2$
. In particular, all the statements in Theorem 7 are also equivalent to a conjecture by Pandharipande and Tseng on the simplest nontrivial genus 1 Gromov-Witten invariant of
$\mathrm {Hilb}(\mathbb {C}^2)$
, namely,
$$ \begin{align*}\langle (2, 1^{d-2})\rangle_{g=1,\beta_n}^{\mathrm{Hilb}^d(\mathbb{C}^2)}. \end{align*} $$
1.7 Plan of the paper
In Section 2, we introduce the morphisms
$\phi $
and
$\varphi $
, which will be useful to deal with the
$\operatorname {NL}_{g,\delta }$
, and explain how they extend to the toroidal compactifications of the various moduli spaces. In Section 3, we use these morphisms to prove Theorem 3 up to the determination of the constant c, which is computed in Section 7. We also show that
$\operatorname {taut}(\alpha \cdot \beta )=0$
for any two cycles supported on the
$\operatorname {NL}_{g,\delta }$
, which is the major step in the proof of Theorem 6. In Section 4, we discuss in more detail the Hecke operators and prove some of their properties. We also prove Theorem 2. In Section 5, we finish the proof of Theorem 6 and explain the connections of the homomorphism property to the kernel of the
$\lambda _g$
-pairing on the moduli space of curves. In Section 6, we explain the connections to Gromov-Witten theory and the proof of Theorem 7.
Throughout the paper we work over the complex numbers, although all the results hold over any algebraically closed field of characteristic
$0$
.
2 The morphisms
$\phi _\delta $
,
$\pi _{\delta }$
and
$\varphi _{g,\delta }$
2.1 Higher degree polarizations
If
$\theta : X \longrightarrow X^\vee $
is a polarization on an abelian variety,
$\ker (\theta )$
carries a symplectic form, and given a Lagrangian subgroup H of
$\ker (\theta )$
, there is a unique principal polarization
$\theta _H$
on
$X/H$
.
If X is an abelian variety with a polarization
$\theta $
of type
$\delta $
, then a level structure for
$\theta $
is a symplectic isomorphism of groups
$$ \begin{align*}f: K(\delta) \stackrel{\cong}{\longrightarrow}\ker (\theta), \end{align*} $$
where
$K(\delta ):=(\mathbb {Z}/d_1 \times \ldots \times \mathbb {Z}/d_g)^2$
carries a canonical symplectic form. The moduli stack of triples
$(X, \theta , f)$
as above is denoted by
$\mathcal A_{g,\delta }^{\mathsf {lev}}$
and it is a smooth Deligne-Mumford stack of dimension
$\binom {g+1}{2}$
.
Definition 3. The morphism
$$ \begin{align*}\phi_\delta : \mathcal A_{g,\delta}^{\mathsf{lev}} \longrightarrow \mathcal A_g \end{align*} $$
is obtained by sending
$(X, \theta ,f)$
to
$(X/f(\{0\} \times \mathbb {Z}^g/\delta ), \theta _{f(\mathbb {Z}^g/\delta \times \{0\})})$
. There is also a morphism
$$ \begin{align*}\pi_\delta : \mathcal A_{g,\delta}^{\mathsf{lev}}\longrightarrow\mathcal A_{g,\delta} \end{align*} $$
that forgets the level structure.
Both
$\phi _\delta $
and
$\pi _\delta $
are finite morphisms, and
$\phi _{\delta }^*{\mathbb E}_g = \pi _\delta ^*{\mathbb E}_{g,\delta }$
, since the Hodge bundle is preserved under isogenies.
Lemma 9. Consider the following groups:
Over the complex numbers, one can realize
$\mathcal A_{g,\delta }$
and
$\mathcal A_{g,\delta }^{\mathsf {lev}}$
as the quotients
$[\mathcal H_g / \mathrm G_{\delta }]$
and
$[\mathcal H_g /\mathrm G_\delta [\delta ]]$
respectively, so that, under this identification,
$\pi _\delta $
and
$\phi _\delta $
are induced by the inclusions
$\mathrm G_{\delta }[\delta ] \subset \mathrm G_{\delta }$
and
$\mathrm G_{\delta }[\delta ] \subset \mathrm {Sp}(2g,\mathbb {Z})$
.
Proof. The stack
$\mathcal A_{g,\delta }^{\mathsf {lev}}$
is explained in [Reference Birkenhake and Lange5, Section 8.3.1.], and from the comments in Section 8.2., it is clear that, in their language,
$\mathcal A_{g,\delta }^{\mathsf {lev}} = [\mathcal H_g / \sigma _{\delta }(\Gamma _\delta (\delta ))]$
, where
One can easily check that
$\sigma _{\delta }(\Gamma _\delta (\delta ))$
is precisely the group
$\mathrm {G}_{g}[\delta ]$
. Under the aforementioned identification,
$\tau \in \mathcal H_g$
corresponds to the triplet
and with this description,
$\phi _\delta $
quotients out the second factor of the kernel of the polarization, so
$\phi _\delta $
sends the polarized abelian variety
$(\mathbb {C}^g /(\tau \, |\, \delta ), \mathrm {Im}(\tau )^{-1})$
to the principally polarized abelian variety 
. Therefore,
$\phi _\delta $
is induced by the identity on
$\mathcal H_g$
. For the map
$\pi _\delta $
this follows from the construction in [Reference Birkenhake and Lange5, Section 8.3.1.].
Proof of Theorem 1.
Theorem 1 holds when
$\delta = (1, \ldots , 1)$
by [Reference van der Geer38, Theorem 3]. For an arbitrary
$\delta $
, consider the diagram
which gives rise to an isomorphism
$$ \begin{align*}\left(\frac{1}{\deg(\pi_\delta)}\pi_{\delta, *}\right) \circ \phi_\delta^* : \mathsf{R}^*(\mathcal A_g) \longrightarrow \mathsf{R}^*(\mathcal A_{g,\delta}) \end{align*} $$
sending
$c_i({\mathbb E}_{g})$
to
$c_i({\mathbb E}_{g,\delta })$
, because the Hodge bundle is preserved by isogenies and so
$\pi _\delta ^* {\mathbb E}_{g,\delta } = \phi _\delta ^*{\mathbb E}_g$
.
2.2 Nonsimple abelian varieties
In this section we introduce the tools to work with the locus of principally polarized abelian varieties having an abelian subvariety. We will see that this is a countable union of substacks of
$\mathcal A_g$
, indexed by the type of the induced polarization on the subvariety.
If
$\delta =(d_1, \ldots , d_u)$
is a polarization type with
$u\leq g/2$
, its complementary type is
$$ \begin{align*}\widetilde{\delta} = (\underbrace{1, \ldots ,1}_{g-2u \text{ times}},d_1, \ldots , d_u), \end{align*} $$
and the double type is
$$ \begin{align*}\delta^2 = (\underbrace{1, \ldots ,1}_{g-2u \text{ times}},d_1,d_1, \ldots ,d_u, d_u). \end{align*} $$
If
$(X, \theta )$
is a principally polarized abelian variety of dimension g and Y is a u-dimensional abelian subvariety, then
$$ \begin{align*}Z:= \ker \left(Y \stackrel{\theta}{\longrightarrow} X^\vee \longrightarrow Y^\vee\right)^{\circ} \end{align*} $$
is the complementary subvariety of Y It has dimension
$g-u$
and by [Reference Birkenhake and Lange5, Lemma 12.1], if
$\theta |_{ Y}$
is of type
$(d_1, \ldots , d_u)$
then
$\theta |_{ Z}$
is of type
$\widetilde {\delta }$
.
Conversely, given polarized abelian varieties
$$ \begin{align*}(X, \theta_X) \in \mathcal A_{u,\delta}\hspace{6pt}\text{ and } \hspace{6pt}(Y, \theta_Y) \in \mathcal A_{g-u, \widetilde{\delta}}, \end{align*} $$
we can construct principally polarized abelian varieties X containing Y and Z as complementary subvarieties with the prescribed polarization. This construction is due to Debarre [Reference Debarre16], and is also explained with detail in [Reference Auffarth4, Section 3]. We summarize the construction in the following lemma, which works in families.
Lemma 10. With notation as above, for any antisymplecticFootnote 3 isomorphism
$$ \begin{align*}p : \ker (\theta_Y) \longrightarrow\ker(\theta_Z), \end{align*} $$
the abelian variety
$$ \begin{align*}\frac{Y \times Z}{\mathrm{graph}(p)} \end{align*} $$
has a canonical principal polarization
$\theta _p$
and contains
$(Y, \theta _Y)$
,
$(Z,\theta _Z)$
as complementary subvarieties. Moreover, the isomorphism type of
$$ \begin{align*}\left(\frac{Y \times Z}{\mathrm{graph}(p)}, \theta_p\right) \end{align*} $$
does not depend on p, and all principally polarized abelian varieties having Y and Z as complementary subvarieties arise this way.
Definition 4. If
$u \leq g/2$
and
$\delta = (d_1, \ldots ,d_u)$
is a polarization type, define the morphism
$$ \begin{align*}\varphi_{g,\delta} : \mathcal A_{u, \delta}^{\mathsf{lev}} \times \mathcal A_{g-u, \widetilde{\delta}}^{\mathsf{lev}} \longrightarrow \mathcal A_g \end{align*} $$
sending the pair
$((Y, \theta _Y , f_Y), (Z, \theta _Z , f_Z))$
to
$$ \begin{align*}\left(\frac{Y \times Z}{\mathrm{graph} (f_Z \circ r \circ f_Y^{-1})},\theta_{f_Z \circ r \circ f_Y^{-1}}\right), \end{align*} $$
where
$$ \begin{align*}r: K(\delta) \longrightarrow K(\widetilde{\delta}) = K(\delta) \end{align*} $$
is the antisymplectic isomorphism that exchanges the factors
$(\mathbb {Z}^g/\delta ) \times 0$
and
$0 \times (\mathbb {Z}^g/\delta )$
. By Lemma 10,
$\varphi _{g,\delta }$
is surjective onto the locus of principally polarized abelian varieties having a subvariety whose induced type is of type
$\delta $
. In particular, this locus is irreducible.
A symplectic automorphism
$ s: K(\delta ) \longrightarrow K(\delta )$
acts on
$\mathcal A_{u, \delta }^{\mathsf {lev}} \times \mathcal A_{g-u, \tilde {\delta }}^{\mathsf {lev}}$
via
$$ \begin{align*}s.((Y, \theta_Y, f_Y), (Z, \theta_Z , f_Z)) = ((Y, \theta_Y , f_Y\circ s^{-1}), (Z, \theta_Z , f_Z\circ s^{-1})), \end{align*} $$
and
$\varphi _{g, \delta }$
is invariant under this action. Let
$\mathcal A_{u, g-u, \delta }$
be the quotient by the action of
$\operatorname {Sp}(K(\delta ))$
just described. It parametrizes triplets
$(X,Y,Z, \theta )$
where
$(X, \theta )$
is a principally polarized abelian variety of dimension g, and Y, Z are complementary subvarieties of a principally polarized abelian variety X, of dimensions u and
$g-u$
, and the type of the induced polarizations
$\theta |_{Y}$
,
$\theta |_{Z}$
is
$\delta $
and
$\widetilde {\delta }$
, respectively.
There is a commutative diagram
and
$\tau $
is a principal
$\operatorname {Sp}(K(\delta ))$
-bundle, so
$\mathcal A_{u, g-u, \delta }$
is a smooth Deligne-Mumford stack.
Let
${\mathbb E}_{u,\delta }$
and
${\mathbb E}_{g-u, \widetilde {\delta }}$
be the pullbacks of the Hodge bundles from
$\mathcal A_{u, \delta }$
and
$\mathcal A_{g-u, \widetilde {\delta }}$
. Then the tangent bundle of
$\mathcal A_{u, g-u, \delta }$
is
$\operatorname {Sym}^2{\mathbb E}_{u, \delta }^\vee \boxplus \operatorname {Sym}^2{\mathbb E}_{g-u, \tilde {\delta }}^\vee $
.
Since the morphism
$\varphi '$
is unramified between smooth DM stacks, it is, étale locally, a regular immersion by [Reference Grothendieck27, Corollary 18.4.7.]. The pullback of the Hodge bundle on
$\mathcal A_g$
via
$\varphi '$
splits as
${\mathbb E}_{u, \delta } \boxtimes {\mathbb E}_{g-u, \tilde {\delta }}$
, so the normal bundle to
$\varphi '$
equals
$$ \begin{align*}N_{\varphi'} = \operatorname{Sym}^2({\mathbb E}_{u, \delta}^\vee \boxtimes {\mathbb E}_{g-u, \tilde{\delta}}^\vee) - \operatorname{Sym}^2{\mathbb E}_{u, \delta}^\vee \boxplus \operatorname{Sym}^2{\mathbb E}_{g-u, \tilde{\delta}}^\vee = {\mathbb E}_{u, \delta}^\vee \boxtimes {\mathbb E}_{g-u, \tilde{\delta}}^\vee. \end{align*} $$
Definition 5.
$\operatorname {NL}_{g,\delta }$
is the stack theoretic image of
$\varphi '$
.
In particular, since generically abelian varieties are simple,
$\varphi '$
has degree
$1$
, so
$$ \begin{align*}[\operatorname{NL}_{g,\delta}] = \varphi^{\prime}_*(\mathbf{1}) = \frac{1}{|\operatorname{Sp}(K(\delta))|} \varphi_{g,\delta, *}(\mathbf{1})\in \mathsf{CH}^{u(g-u)}(\mathcal A_g). \end{align*} $$
Remark 11. When
$u = g/2$
,
$\varphi '$
has degree
$2$
because one can exchange the role of Y and Z so
$[\operatorname {NL}_{g,\delta }]$
should be
$\frac {1}{2}\varphi ^{\prime }_*(\mathbf {1})$
in principle. However, it is more convenient to consider
$$ \begin{align*}[\operatorname{NL}_{g,\delta}] := \varphi^{\prime}_*(\mathbf{1}). \end{align*} $$
This is consistent with [Reference Canning, Oprea and Pandharipande15, Reference Canning, Molcho, Oprea and Pandharipande14], where the cycle classes
$[\mathcal A_{g/2} \times \mathcal A_{g/2}]$
are the pushforward of
$1$
along
$\mathcal A_{g/2} \times \mathcal A_{g/2} \longrightarrow \mathcal A_g$
.
2.3 Extensions to the boundary
Mumford and his collaborators introduce in [Reference Ash, Mumford, Rapoport and Tai3] various toroidal compactifications of the quotient of a hermitian symmetric domain
$\mathcal D$
(such as the Siegel upper half space) by an arithmetic subgroup
$\Gamma $
of its group of automorphisms. These compactifications depend on a choice of a
$\Gamma $
-admissible subdivision
$\Sigma $
of a certain cone. The resulting proper space is denoted by
$$ \begin{align*}\overline{[\mathcal D/\Gamma]}^\Sigma. \end{align*} $$
If
$\mathcal D = G/K$
, where K is a maximal compact subgroup, complex representations of K give rise to automorphic bundles on
$[\mathcal D/\Gamma ]$
, such as the Hodge bundle (which arises as the defining representation of
$U(g) \subseteq \operatorname {Sp}(2g, \mathbb R)$
on
$\mathbb C^g$
). These bundles have a canonical extension to any toroidal compactification [Reference Mumford32]. We denote the extension of the Hodge bundle by
${\mathbb E}_g$
.
The morphisms
$\pi _\delta $
,
$\phi _\delta $
and
$\varphi _{g, \delta }$
extend to arbitrarily fine toroidal compactifications of the moduli spaces. This follows from the results in [Reference Harris28], so it might be clear to experts, but we explain it in detail.
Given two arithmetic subgroups
$\Gamma < \Gamma '$
for a hermitian symmetric domain
$\mathcal D$
, any subdivision
$\Sigma $
which is
$\Gamma '$
-admissible is also
$\Gamma $
-admissible and the map
$$ \begin{align*}\overline{[\mathcal D/\Gamma]}^{\Sigma} \longrightarrow \overline{[\mathcal D/\Gamma']}^{\Sigma} \end{align*} $$
is well-defined. The morphisms
$\pi _\delta $
and
$\phi _\delta $
are quotients by a finite subgroup, so their extendability is proven.
For
$\varphi _{g,\delta }$
, note that we can factor it as
$$ \begin{align*}\mathcal A_{u, \delta}^{\mathsf{lev}} \times \mathcal A_{g-u, \widetilde{\delta}}^{\mathsf{lev}}\stackrel{\iota}{\longrightarrow} \mathcal A_{g, \delta^2}^{\mathsf{lev}} \stackrel{\kappa}{\longrightarrow} \mathcal A_{g} \end{align*} $$
where
$\iota $
takes two polarized abelian varieties to their product, which is polarized by the product of the two polarizations, and sends two bases of the kernels of the polarizations to their union, and
$\kappa $
sends an abelian variety to its quotient by the antidiagonal of the identity
$K(\delta ) \longrightarrow K(\delta )$
, seen as a subset of
$K(\delta ^2)$
. Then,
$\kappa $
is just a quotient by a congruence subgroup as before, and with the identifications as in Lemma 9,
$\iota $
is induced by the map
$$ \begin{align*} \mathcal H_u \times \mathcal H_{g-u} &\longrightarrow \quad \mathcal H_g\\(\tau', \tau")\quad &\mapsto \ \begin{pmatrix} \tau' &0\\ 0&\tau" \end{pmatrix} , \end{align*} $$
which is a morphism of hermitian symmetric domains, and so
$\iota $
extends to arbitrary toroidal compactifications by the explanation in [Reference Harris28, Section 3.3.]. The operations of pulling back an automorphic bundle by (an extension of) a morphism of hermitian symmetric domain of an automorphic bundle and taking canonical extensions commute by [Reference Harris28, Theorem 4.2.] and so,
$$ \begin{align*}\overline{\varphi}_{g, \delta}^* {\mathbb E}_g = {\mathbb E}_u \boxplus {\mathbb E}_{g-u} \quad \overline{\pi}_{\delta}^* {\mathbb E}_g = {\mathbb E}_g \quad \overline{\phi}^*_\delta {\mathbb E}_g = {\mathbb E}_g . \end{align*} $$
3 Intersection properties of
$\operatorname {NL}_{g,\delta }$
3.1 Tautological projection
Recall that the tautological projection
$\operatorname {taut}(\alpha )$
is the unique tautological class such that
$$ \begin{align*}\int_{\overline{\mathcal A}_g} \overline{\alpha} \cdot \Lambda \cdot \lambda_g = \int_{\overline{\mathcal A}_g} \operatorname{taut}(\alpha) \cdot \Lambda \cdot \lambda_g \end{align*} $$
for any tautological class
$\Lambda \in \mathsf {R}^*(\mathcal A_g)$
, where
$\overline {\alpha }$
is an extension of
$\alpha $
to
$\overline {\mathcal A}_g$
.
Proof of Theorem 3.
Consider extensions of the morphisms
$\phi _\delta \times \phi _{\tilde {\delta }}$
and
$\varphi _{g, \delta }$
as discussed in Section 2.3, so that there is a commutative diagram
and the pullbacks of the Hodge bundle to
$\overline {\mathcal A_{u,\delta }^{\mathsf {lev}} \times \mathcal A_{g-u, \tilde {\delta }}^{\mathsf {lev}}}$
agree. Then
$\overline {\varphi }_{g, \delta , *}(1)$
is an extension of
$[\operatorname {NL}_{g,\delta }]$
. If
$\Lambda $
is a tautological class, and we write
$\Lambda \cdot \lambda _{g} = P(c_1({\mathbb E}_g), \ldots , c_g({\mathbb E}_g))$
,
$$ \begin{align*} \int_{\overline{\mathcal A}^{\Sigma_1}_g} \overline{[\operatorname{NL}_{g, \delta}]} \cdot \Lambda \cdot \lambda_g & = \frac{1}{\deg (\overline{\varphi}_{g, \delta})}\int_{\overline{\mathcal A}_g} \overline{\varphi}_{g, \delta, *}(1) \cdot P(c_i({\mathbb E}_g))\\ &= \frac{1}{\deg (\overline{\varphi}_{g, \delta})}\int_{\overline{\mathcal A_{u,\delta}^{\mathsf{lev}} \times \mathcal A_{g-u, \tilde{\delta}}^{\mathsf{lev}}}} P(c_i(\overline{\varphi}_{g, \delta}^*{\mathbb E}_g))\\ &= \frac{1}{\deg (\overline{\varphi}_{g, \delta})}\int_{\overline{\mathcal A_{u,\delta}^{\mathsf{lev}} \times \mathcal A_{g-u, \tilde{\delta}}^{\mathsf{lev}}}} P(c_i(\overline{\phi_{\delta}\times \phi_{\tilde{\delta}}}^*({\mathbb E}_u \boxplus {\mathbb E}_{g-u})))\\ &=\frac{\deg (\overline{\phi_{\delta}\times \phi_{ \tilde{\delta}})}}{\deg (\overline{\varphi}_{g, \delta})}\int_{\overline{\mathcal A_u \times \mathcal A_{g-u}}} P(c_i({\mathbb E}_u \boxplus {\mathbb E}_{g-u}))\\ &=\frac{\deg (\overline{\phi_{\delta}\times \phi_{ \tilde{\delta}})}}{\deg (\overline{\varphi}_{g, \delta})} \int_{\overline{\mathcal A_u \times \mathcal A_{g-u}}} P(c_i(\overline{\varphi}_{g, (1^u)}^*{\mathbb E}_g))\\& = \frac{\deg (\overline{\phi_{\delta}\times \phi_{ \tilde{\delta}})}}{\deg (\overline{\varphi}_{g, \delta})} \int_{\overline{\mathcal A}^{\Sigma_2}_g} \overline{[\mathcal A_u \times \mathcal A_{g-u}]} \cdot \Lambda \cdot \lambda_g\\ &= \frac{\deg (\overline{\phi_{\delta}\times \phi_{ \tilde{\delta}})}}{\deg (\overline{\varphi}_{g, \delta})} \int_{\overline{\mathcal A}^{\Sigma_2}_g} \operatorname{taut}([\mathcal A_u \times \mathcal A_{g-u}]) \cdot \Lambda \cdot \lambda_g \\ &= \int_{\overline{\mathcal A}^{\Sigma_1}_g} \frac{\deg (\overline{\phi_{\delta}\times \phi_{ \tilde{\delta}})}}{\deg (\overline{\varphi}_{g, \delta})} \operatorname{taut}([\mathcal A_u \times \mathcal A_{g-u}]) \cdot \Lambda \cdot \lambda_g, \end{align*} $$
by several applications of the projection formula. Note also that
$$ \begin{align*}\frac{\deg (\overline{\phi_{\delta}\times \phi_{ \tilde{\delta}})}}{\deg (\overline{\varphi}_{g, \delta})} = \frac{\deg (\phi_{\delta})\cdot\deg( \phi_{\tilde{\delta}})}{\deg (\varphi_{g, \delta})} = \frac{\deg (\phi_{\delta})\cdot\deg( \phi_{\tilde{\delta}})}{|\operatorname{Sp}(K(\delta))|}. \end{align*} $$
by Lemma 10, and these numbers are calculated in Propositions 26 and 27.
Remark 12. When
$u=1$
, one can prove that the tautological projections of all the
$[\operatorname {NL}_{g,d}]$
are proportional to
$\lambda _{g-1}$
in a different way:
$$ \begin{align*} \lambda_{g-1}\cdot [\operatorname{NL}_{g,d}] &= \frac{1}{\deg(\varphi_{g,d})}\varphi_{g,d,*}\varphi_{g,d}^*\lambda_{g-1} = \frac{1}{\deg(\varphi_{d,g})}\varphi_{g,d,*} c_{g-1}({\mathbb E}_1 \boxplus {\mathbb E}_{g-1})\\ &= \frac{1}{\deg(\varphi_{g,d})}\varphi_{g,d,*}(c_1({\mathbb E}_1)c_{g-2}({\mathbb E}_{g-1}) + c_{g-1}({\mathbb E}_{g-1}))=0, \end{align*} $$
where we are using Theorem 1. Therefore,
$$ \begin{align*} \lambda_{g-1} \operatorname{taut}(\operatorname{NL}_{g,d}) = \operatorname{taut}(\lambda_{g-1} \cdot [\operatorname{NL}_{g,d}])=0, \end{align*} $$
by formula (1.5); but
$\mathbb {Q}\lambda _{g-1}\subset \mathsf {R}^{g-1}(\mathcal A_{g})$
is precisely the kernel of the map that sends
$\alpha $
to
$\alpha \cdot \lambda _{g-1}$
. This was pointed out by R. Pandharipande.
Proof of Corollary 4.
Given a homomorphism
$f: E \longrightarrow (A,\theta )$
, let
$d = \deg (f^*\theta )$
and
$\hat {d} = d/|\ker (f)|$
. This defines an elliptic subgroup
$E'$
of A such that
$\theta _{E'}$
is of type
$\hat {d}$
. Conversely, given an elliptic subgroup
$E'\leq A$
, there are
$\sigma _1(d/\hat {d})$
isogenies
$E \longrightarrow E'$
of degree
$d/\hat {d}$
, where
$\sigma _k(n) = \sum _{m \mid n} m^k$
. Therefore,
$$ \begin{align} [\widetilde{\operatorname{NL}}_{g,d}] = \sum_{\hat{d}\mid d}\sigma_1(d/\hat{d})[\operatorname{NL}_{g,\hat{d}}], \end{align} $$
and, by Theorem 3,
$$ \begin{align*} \operatorname{taut}([\widetilde{\operatorname{NL}}_{g,d}]) &=\frac{g}{6|B_{2g}|}\sum_{\hat{d}\mid d}\sigma_{1}(d/\hat{d})d^{2g-1}\prod_{p \mid \hat{d}}(1-p^{2g-2}) \lambda_{g-1}\\ &= \frac{g}{6|B_{2g}|}d\sum_{\hat{d}\mid d}\sigma_{-1}(d/\hat{d}) \hat{d}^{2g-2}\prod_{p \mid \hat{d}}(1-p^{2g-2})\lambda_{g-1}. \end{align*} $$
The function
$n \mapsto n^k \prod _{p \mid n} (1-p^{-k})$
is Jacobi’s totient function
$J_k$
, and can also be written as a convolution
$\operatorname {Id}_k * \mu $
, where
$\operatorname {Id}_k(n)=n^k$
and
$\mu $
is the Möbius inversion function. By basic convolution identities, we have that
$$ \begin{align*}d\cdot (\sigma_{-1}*J_{2g-2})(d)=d\cdot (\operatorname{Id}_{-1} * 1*\mu*\operatorname{Id}_{2g-2})(d) = d\cdot (\operatorname{Id}_{-1}*\operatorname{Id}_{2g-2})(d) = \sigma_{2g-1}(d).\\[-38pt] \end{align*} $$
3.2 Intersections between
$\operatorname {NL}$
cycles
In [Reference Canning, Oprea and Pandharipande15] the authors use the excess intersection formula to show that
$[\mathcal A_{g_1}\times \ldots \times \mathcal A_{g_l}] \cdot [\mathcal A_{h_1}\times \ldots \mathcal A_{h_k}]=0$
. More generally, we study the intersection of any pair of cycles supported on the
$\operatorname {NL}$
locus.
Proposition 13. Let
$u\leq v \leq g/2$
and
$\delta = (d_1, \ldots , d_u)$
,
$\varepsilon = (e_1, \ldots , e_v)$
be polarization types. Suppose that
$\gamma , \eta $
are two cycles supported on
$\operatorname {NL}_{g, \delta }$
and
$\operatorname {NL}_{g, \varepsilon }$
, respectively. Then
$$ \begin{align*}\operatorname{taut}(\gamma \cdot \eta) =0. \end{align*} $$
Proof. We form the Cartesian diagram
$\mathcal Z$
parametrizes the data of an abelian variety with two pairs of complementary subgroups. The different incidences between these subgroups determine disconnected components of
$\mathcal Z$
. More concretely, let
$X \sim X_1\times X_2 \sim Y_1 \times Y_2$
, where
$\dim (X_1)=u$
,
$\dim (Y_1) =v$
and
$\sim $
denotes an isogeny. Up to isogeny, we have maps
$$ \begin{align*}\pi_1, \pi_2 : X_1 \longrightarrow Y_1, Y_2 \end{align*} $$
and
$\ker (\pi _1) \cap \ker (\pi _2)$
is a finite group, so
$$ \begin{align*} X_1 &\sim \ker (\pi_1) \times \ker (\pi_2) \times E,\\ Y_1 &\sim \ker (\pi_2) \times E \times D_1,\\ Y_2 & \sim \ker(\pi_1) \times E \times D_2,\\ X_2 &\sim E \times D_1 \times D_2, \end{align*} $$
for some abelian varieties
$E, D_1, D_2$
. Note that the isogeny class of E appears twice in the isogeny class of X. From the way we have constructed these varieties, it is clear that the dimensions of
$E, D_1, D_2, \ker (\pi _1), \ker (\pi _2)$
stay constant if X moves along a connected component of
$\mathcal Z$
. There are discrete invariants involving the types of the different polarizations induced on each of the varieties. The construction of
$\varphi _{g,\delta }$
in Section 2.2 can be generalized, without having as much control on the degrees of the morphisms. After adding a large enough level structure, the abelian variety X, with its subvarieties
$X_i, Y_i$
, can be recovered from some polarized abelian varieties
$X_i', Y_i'$
which are isogenous to
$X_i$
and
$Y_i$
respectively, with bounded isogeny degree, and with a level structure on
$X_i'$
and
$Y_i'$
.
Therefore, each connected component of
$\mathcal Z$
has a finite morphism from
$$ \begin{align} \mathcal W := \mathcal A_{n_1,\mathsf{lev}}\times \mathcal A_{n_2,\mathsf{lev}}\times\mathcal A_{m_1,\mathsf{lev}}\times\mathcal A_{m_2,\mathsf{lev}}\times\mathcal A_{p,\mathsf{lev}}, , \end{align} $$
where
$n_i = \dim (\ker (\pi _i))$
,
$m_i = \dim (D_i)$
and
$p = \dim (E)$
, and
$\mathcal A_{h,\mathsf {lev}}$
denotes a (connected) moduli space of polarized abelian varieties of dimension h with some level structureFootnote
4
, so that the maps to
$\mathcal A_{v, g-v, \varepsilon }$
and
$\mathcal A_{u, g-u, \delta }$
(which we will think about for the rest of the section as
$\mathcal A_{v,\mathsf {lev}} \times \mathcal A_{g-v, \mathsf {lev}}$
and
$\mathcal A_{u,\mathsf {lev}} \times \mathcal A_{g-u, \mathsf {lev}}$
respectively) factor as the diagonal on
$\mathcal A_{p,\mathsf {lev}}$
:
$$ \begin{align*}\Delta : \mathcal W \longrightarrow \mathcal V:=\mathcal A_{n_1,\mathsf{lev}}\times \mathcal A_{n_2,\mathsf{lev}}\times\mathcal A_{m_1,\mathsf{lev}}\times\mathcal A_{m_2,\mathsf{lev}}\times\mathcal A_{p,\mathsf{lev}} \times \mathcal A_{p,\mathsf{lev}} \end{align*} $$
followed by multiplication maps
$$ \begin{align*} \mathcal V & \stackrel{\mathrm{mult}_1}{\longrightarrow} \mathcal A_{v, \mathsf{lev}}\times \mathcal A_{g-v,\mathsf{lev}} \\(K_1, K_2, D_1, D_2, E_1, E_2) & \mapsto{} \ \ (K_2\times D_1 \times E_1, K_1 \times D_2 \times E_2) , \end{align*} $$
$$ \begin{align*} \mathcal V & \stackrel{\mathrm{mult}_2}{\longrightarrow} \mathcal A_{u, \mathsf{lev}}\times \mathcal A_{g-u,\mathsf{lev}} \\(K_1, K_2, D_1, D_2, E_1, E_2) & \mapsto{} \ \ (K_1\times K_2 \times E_1, D_1 \times D_2 \times E_2) , \end{align*} $$
and possibly quotient maps such as
$\phi _\delta $
or
$\pi _\delta $
that forget level structure or send an abelian variety to the quotient of it by a finite group. We will omit these since they do not play a role in the computation.
We do this in detail when
$\varepsilon = (1, \ldots , 1)$
and
$u=1$
, which is the only statement that we need for Theorem 7. In this case,
$\mathcal Z$
parametrizes principally polarized abelian varieties
$X = Y_1 \times Y_2$
that have an elliptic subgroup
$X_1$
such that
$\theta _X \cdot X_1 = d$
. If
$\pi _1(X_1)=0$
then
$Y_2 \in \operatorname {NL}_{v,d}$
and the map
$$ \begin{align*}\operatorname{NL}_{v,d} \times \mathcal A_{g-v} \longrightarrow\mathcal Z \end{align*} $$
is an isomorphism onto a connected component, and so we have a finite map
$$ \begin{align*}\mathcal A_{v-1,(1,\ldots , 1,d)}^{\mathsf{lev}} \times \mathcal A_{1,(d)}^{\mathsf{lev}} \times \mathcal A_{g-v} \longrightarrow \mathcal Z . \end{align*} $$
Similarly if
$\pi _2(X_1)=0$
. Otherwise,
$\pi _1$
and
$\pi _2$
are nonzero maps. Define the discrete data
$G_i = \ker (\pi _i)$
,
$d_i = |G_i|$
and
$f_i = \pi _i(X_1)\cdot \theta _{X_i}$
, so that
$$ \begin{align*}G_1 \cap G_2 =\{0\}, \pi_i(X_1) = X_1/G_i \text{ and } d =d_1f_1 + d_2f_2 . \end{align*} $$
Consider the modular curve
$$ \begin{align*}\mathcal A_{1,G_1,G_2, f_1, f_2}^{\mathsf{lev}} \end{align*} $$
that parametrizes elliptic curves
$X_1'$
with a pair of subgroups
$G_1', G_2'$
, isomorphic to
$G_1$
and
$G_2$
as abstract groups that intersect trivially and a basis of the
$f_1$
-torsion points of
$X_1'/G_1'$
, and a basis of the
$f_2$
-torsion points of
$X_1'/G_2'$
. This modular curve is a finite cover of
$\mathcal A_1$
, and has a “diagonal” map
$$ \begin{align*} \Delta : \mathcal A_{1,G_1,G_2, f_1, f_2}^{\mathsf{lev}} & \longrightarrow \mathcal A_{1,(f_1)}^{\mathsf{lev}} \times \mathcal A_{1,(f_2)}^{\mathsf{lev}}\\(X_1', G_1', G_2') &\mapsto \ \ (X_1'/G_1', X_1'/G_2') . \end{align*} $$
and
$(\varphi _{v,(f_1)} \times \varphi _{g-v, (f_2)}) \circ \Delta $
maps to
$\mathcal Z$
, and is surjective onto the connected component with discrete data defined above. The reason why
$\Delta $
is a “diagonal” map is because if
$N= d_1d_2f_1^2f_2^2$
then there is a finite étale map
$$ \begin{align*}\kappa: \mathcal A_{1,(N)}^{\mathsf{lev}} \longrightarrow \mathcal A_{1,G_1,G_2, f_1, f_2}^{\mathsf{lev}}, \end{align*} $$
obtained by choosing particular subgroups of
$(\mathbb {Z}/N\mathbb {Z})^2$
which are isomorphic to
$G_1$
and
$G_2$
and are disjoint, and elements of
$(\mathbb {Z}/N\mathbb {Z})^2$
that give symplectic basis of the
$f_1$
and
$f_2$
-torsion points of the quotients of
$(\mathbb {Z}/N\mathbb {Z})^2$
by these subgroups, and then, we can factor
$\Delta \circ \kappa $
as an honest diagonal map
$$ \begin{align*}\mathcal A_{1,(N)}^{\mathsf{lev}} \longrightarrow \mathcal A_{1,(N)}^{\mathsf{lev}} \times \mathcal A_{1,(N)}^{\mathsf{lev}} \end{align*} $$
and other finite maps, which quotient by the relevant subgroups.
Going back to the general situation, the normal bundle to the composite morphism
$$ \begin{align*}\mathcal W \stackrel{\Delta}{\longrightarrow} \mathcal V \stackrel{\mathrm{mult}_1}{\longrightarrow} \mathcal A_{v, \mathsf{lev}}\times \mathcal A_{g-v,\mathsf{lev}} \end{align*} $$
is
$$ \begin{align*} N_{\Delta} + \Delta^* N_{\mathrm{mult}_1} &= \operatorname{Sym}^2 {\mathbb E}_p^\vee + {\mathbb E}_{n_2}^\vee \boxtimes {\mathbb E}_{m_1}^\vee+ {\mathbb E}_{n_2}^\vee \boxtimes {\mathbb E}_{p}^\vee+ {\mathbb E}_{p}^\vee \boxtimes {\mathbb E}_{m_1}^\vee\\ &+{\mathbb E}_{n_1}^\vee \boxtimes {\mathbb E}_{m_2}^\vee+ {\mathbb E}_{n_1}^\vee \boxtimes {\mathbb E}_{p}^\vee+ {\mathbb E}_{p}^\vee \boxtimes {\mathbb E}_{m_2}^\vee, \end{align*} $$
And the pullback via
$\mathrm {mult}_2 \circ \Delta $
of the normal bundle to
$$ \begin{align*}\mathcal A_{u, \mathsf{lev}}\times \mathcal A_{g-u, \mathsf{lev}} \longrightarrow\mathcal A_g \end{align*} $$
is
$$ \begin{align*} (\mathrm{mult}_2 \circ \Delta)^* ({\mathbb E}_{u}^\vee \boxtimes {\mathbb E}_{g-u}^\vee)&=({\mathbb E}_{n_1}^\vee + {\mathbb E}_{n_2}^\vee +{\mathbb E}_{p}^\vee)\boxtimes({\mathbb E}_{m_1}^\vee + {\mathbb E}_{m_2}^\vee +{\mathbb E}_{p}^\vee)\\ &= {\mathbb E}_{n_1}^\vee \boxtimes {\mathbb E}_{m_1}^\vee+ {\mathbb E}_{n_1}^\vee \boxtimes {\mathbb E}_{m_2}^\vee+ {\mathbb E}_{n_1}^\vee \boxtimes {\mathbb E}_{p}^\vee + {\mathbb E}_{n_2}^\vee \boxtimes {\mathbb E}_{m_1}^\vee\\ &+{\mathbb E}_{n_2}^\vee \boxtimes {\mathbb E}_{m_2}^\vee+ {\mathbb E}_{n_2}^\vee \boxtimes {\mathbb E}_{p}^\vee + {\mathbb E}_{p}^\vee \boxtimes {\mathbb E}_{m_1}^\vee+ {\mathbb E}_{p}^\vee \boxtimes {\mathbb E}_{m_2}^\vee+ {\mathbb E}_{p}^\vee \boxtimes {\mathbb E}_{p}^\vee. \end{align*} $$
Therefore, the excess bundle is
$$ \begin{align*}\mathrm{Exc}_{\mathcal W} = {\mathbb E}_{n_1}^\vee \boxtimes {\mathbb E}_{m_1}^\vee + {\mathbb E}_{n_2}^\vee \boxtimes {\mathbb E}_{m_2}^\vee + \wedge^2{\mathbb E}_p^\vee. \end{align*} $$
Note that if
$V,W$
are two vector bundles then
$$ \begin{align*}c_{top}(V)=c_{top}(W) = 0 \Rightarrow c_{top}(V \otimes W)=0, \text{ and } c_{top}(V)=0 \text{ or }c_{top}(W)=0 \Rightarrow c_{top}(V \oplus W)=0. \end{align*} $$
The top Chern class of the Hodge bundle vanishes on any moduli space of abelian varieties of dimension
$>0$
, so by the excess intersection formula [Reference Fulton23, Theorem 6.2.], the Gysin pullback
$\varphi _{g,\delta }^!$
in (3.2) is zero when restricted to a component
$\mathcal W$
as above with
$n_1m_1 \neq 0$
or
$n_2m_2 \neq 0$
.
Since
$$ \begin{align*}\begin{array}{cc} u=n_1 +n_2 +p & v=n_2+m_1+p \\ g-u= m_1 +m_2 +p & g-v = n_1 +m_2 +p \end{array}\!, \end{align*} $$
we cannot have
$n_1m_1=n_2m_2=p=0$
, so the components
$\mathcal W$
where
$\varphi _{g,\delta }^!$
could be nonzero satisfy
$p\geq 1$
.
Let
$\mathcal W$
be a component with
$n_1m_1 = n_2m_2 =0$
,
$p>0$
. Just as we did in Section 2.3, the morphisms
$\mathrm {mult}_i, \varphi _{g, \varepsilon }$
can be extended to sufficiently fine toroidal compactifications, while still preserving the splitting of the pullback of the Hodge bundle:
$$ \begin{align*}\overline{\mathcal W} \stackrel{\overline{\mathrm{mult}}_i \circ \overline{\Delta}}{\longrightarrow} \overline{\mathcal A_{v, \mathsf{lev}}\times \mathcal A_{g-v,\mathsf{lev}}} \stackrel{\overline{\varphi}_{g,\delta}}{\longrightarrow} \overline{\mathcal A}_g. \end{align*} $$
There is a cycle
$\alpha _W$
on
$\mathsf {CH}_*(\mathcal {W})$
whose pushforward to
$\mathcal A_g$
is the contribution of
$\mathcal {W}$
to
$[\operatorname {NL}_{g,\delta }]\cdot [\operatorname {NL}_{g, \varepsilon }]$
. If we take an extension
$\overline {\alpha }_{\mathcal W}$
of
$\alpha _{\mathcal W}$
to
$\mathsf {CH}_*(\overline {\mathcal {W}})$
, then the sum of the pushforwards of all the
$\overline {\alpha }_{\mathcal W}$
will be an extension of
$[\operatorname {NL}_{g,\delta }]\cdot [\operatorname {NL}_{g, \varepsilon }]$
to
$\mathsf {CH}_*(\overline {\mathcal A_g})$
. The tautological projection of
$[\operatorname {NL}_{g,\delta }]\cdot [\operatorname {NL}_{g, \varepsilon }]$
can be computed from integrals of the form
$$ \begin{align*} \int_{\overline{\mathcal A}_g} \sum_{\mathcal W\text{ with }p \geq 1} (\overline{\mathrm{mult}}_i\circ \overline{\Delta}\circ \overline{\varphi}_{g,\delta})_*(\overline{\alpha}_\mathcal W)\cdot P(\lambda_i)\cdot c_{top}({\mathbb E}_g). \end{align*} $$
However,
$$ \begin{align*} (\overline{\mathrm{mult}}_i\circ {\overline{\Delta}}\circ {\overline{\varphi}}_{g,\delta})^*{\mathbb E}_g = {\mathbb E}_p^2 \oplus {\mathbb E}_{n_1} \oplus {\mathbb E}_{n_2} \oplus {\mathbb E}_{m_1} \oplus {\mathbb E}_{m_2} \end{align*} $$
has vanishing top Chern class, since
$c_p({\mathbb E}_p)^2 =0$
, on
$\overline {\mathcal A}_{p, \mathsf {lev}}$
by Mumford’s relation [Reference Esnault and Viehweg20].
For arbitrary cycles
$\gamma , \eta $
supported on
$\operatorname {NL}_{g, \varepsilon }$
and
$\operatorname {NL}_{g, \delta }$
,
$\overline {\gamma \cdot \eta }$
is the pushforward to
$\mathcal A_g$
of a cycle supported on components
$\overline {\mathcal W}$
with
$p>0$
, and the same argument applies.
The intersection product
$[\operatorname {NL}_{g, \delta }]\cdot [\operatorname {NL}_{g, \varepsilon }]$
is the sum, over all components
$\mathcal W$
of
$\mathcal Z$
of a rational multiple of
$$ \begin{align*}\mathrm{mult}_{1,*}(\Delta_*(c_{top}( \mathrm{Exc}_{\mathcal W}) \cap \Delta^!(\mathrm{mult}_1^!(1)))) = \begin{cases} \mathrm{mult}_{1,*}(\Delta_*(c_{top}(\wedge^2{\mathbb E}_p^\vee))) &\text{ if }n_1m_1=n_2m_2=0,\\ 0&\text{ otherwise.} \end{cases} \end{align*} $$
Lemma 14. If
$1 \leq p \leq 3$
, and
$$ \begin{align*}\Delta_{\mathcal A_{p,\mathsf{lev}}} : \mathcal A_{p,\mathsf{lev}} \longrightarrow\mathcal A_{p,\mathsf{lev}} \times \mathcal A_{p,\mathsf{lev}} \end{align*} $$
is the diagonal, then
$$ \begin{align*}\Delta_{\mathcal A_{p,\mathsf{lev}},*}(c_{top}(\wedge^2 {\mathbb E}^\vee_p)) =0. \end{align*} $$
Proof. The Chow groups of
$\mathcal A_1, \mathcal A_2, \mathcal A_3$
have been determined, and they are equal to their tautological rings. Moreover, the stacks
$\mathcal A_1, \mathcal A_2$
and
$\mathcal A_3$
have the Chow-Kunneth generation property (see [Reference Bae and Schmitt11, Definition 2.5.]) because
$\mathcal M_{1,1}$
,
$\mathcal M_2^{ct}$
and
$\mathcal M_3^{ct}$
have it, from their stratifications as quotients of open subsets of affine space, and so
$$ \begin{align*}\mathsf{R}^*(\mathcal A_p) \otimes \mathsf{R}^*(\mathcal A_p) \longrightarrow \mathsf{CH}^*(\mathcal A_p \times \mathcal A_p) \end{align*} $$
is surjective. Since
$\mathsf {R}^{>{\binom {p}{2}}}(\mathcal A_p) =0$
, we see that
$\mathsf {CH}_{<2{\binom {p+1}{2}}-2\binom {p}{2}}(\mathcal A_p \times \mathcal A_p)=0$
. In particular,
$\mathsf {CH}_p(\mathcal A_p \times \mathcal A_p)=0$
for
$p=1,2,3$
. For a moduli stack with level structure, we can form a Cartesian diagram
The Hodge bundle pulls back to the Hodge bundle under
$\pi $
, so the result follows from the formula
$(\pi \times \pi )^* \circ \Delta _{\mathcal A_g,*} = \Delta _{\mathcal A_{g,\mathsf {lev}}, *} \circ \pi ^*$
. If
$\mathcal A_{p,\mathsf {lev}}$
does not map to
$\mathcal A_p$
, we can always find some
$\mathcal A_{p, \mathsf {lev}'}$
that dominates both, and repeat the argument.
This proves the following:
Proposition 15. Let
$u\leq v \leq g/2$
and
$\delta = (d_1, \ldots , d_u)$
,
$\epsilon _v = (e_1, \ldots , e_v)$
be polarization types. If
$u \leq 3$
then
$$ \begin{align*}[\operatorname{NL}_{g, \delta}]\cdot [\operatorname{NL}_{g, \varepsilon}] =0 \end{align*} $$
in the Chow groups of
$\mathcal A_g$
.
Remark 16. For
$p=4,5$
, the stacks of Prym curves
$\mathcal R_{p+1}$
have unirational parametrizations, so it is not unreasonable to expect that they have the Chow-Kunneth generation property, and that one can calculate their Chow groups, hoping that they are tautological, and that the same holds for
$\mathcal A_p$
since there are dominant maps
$\mathcal R_{p+1} \longrightarrow \mathcal A_p$
. This would show that Lemma 14 holds for
$p \leq 5$
, and so Proposition 15 is likely true for
$u \leq 5$
. It would be interesting to see if this is true for any u, and this requires a new idea, since
$\mathcal A_6$
is not unirational [Reference Dittmann, Manni and Scheithauer19] and has nontautological algebraic classes [Reference Canning, Oprea and Pandharipande15].
4 The Hecke algebra
For each
$n \geq 1$
, let
$$ \begin{align*}\mathcal B_{g, n} = \left\lbrace \begin{array}{l} \text{homomorphisms }f:(X, \theta_X) \longrightarrow(Y, \theta_Y)\\\text{such that } (X, \theta_X), (Y, \theta_Y) \in \mathcal A_g\text{ and }f^*\theta_Y = n\theta_X \end{array}\right\rbrace. \end{align*} $$
It is a smooth DM stack and has forgetful maps
which are étale, and induce Hecke operators
$$ \begin{align*}T_n := \pi_{2,*} \circ \pi_1^* : \mathsf{CH}^*(\mathcal A_g)\longrightarrow\mathsf{CH}^*(\mathcal A_g). \end{align*} $$
Let
$\operatorname {vol}(T_n) = T_n(\mathbf {1}) \in \mathbb {Z}$
be the volume of
$T_n$
, which is computed in Proposition 28:
$$ \begin{align*}\operatorname{vol} (T_n) = \prod_{p \mid n}\prod_{i=1}^g\frac{1-p^{g(v_p(n)+i)}}{1-p^{gi}}. \end{align*} $$
It is clear that
$T_n$
maps tautological classes to tautological classes, since the Hodge bundle is invariant under isogenies. In fact, they are eigenvectors of all the
$T_n$
with eigenvalues
$\operatorname {vol}(T_n)$
.
Lemma 17. The tautological projection commutes with the Hecke operators.
Proof.
$\pi _1$
and
$\pi _2$
are morphisms of locally symmetric domains, so by what we explained in Section 2.3, they extend to sufficiently fine toroidal compactifications, and the extensions satisfy
$\overline {\pi }_1^*{\mathbb E}_g = \overline {\pi }_2^* {\mathbb E}_g$
, so if
$\alpha \in \mathsf {CH}^*(\mathcal A_g)$
and
$\Lambda $
is a tautological class,
$$ \begin{align*} \int_{\overline{\mathcal A}_g} \operatorname{taut}\left( T_n(\alpha)\right)\Lambda \lambda_g &= \int_{\overline{\mathcal A}_g}\overline{T_n(\alpha)} \Lambda \lambda_g = \int_{\overline{\mathcal A}_g}T_n(\overline{\alpha}) \Lambda \lambda_g =\int_{\overline{\mathcal A}_g} \overline{\pi}_{2,*}(\overline{\pi}_1^*\alpha)\Lambda \lambda_g\\ &= \int_{\overline{\mathcal B}_{g,n}} \overline{\pi}_1^*\alpha \cdot \overline{\pi}_{2}^*(\Lambda \lambda_g) = \int_{\overline{\mathcal B}_{g,n}} \overline{\pi}_1^*(\alpha\cdot \Lambda \lambda_g)=\operatorname{vol}(T_n) \int_{\overline{\mathcal A}_g}\overline{\alpha} \Lambda \lambda_g \\ &= \operatorname{vol}(T_n) \int_{\overline{\mathcal A}_g}\operatorname{taut}(\alpha) \Lambda \lambda_g = \int_{\overline{\mathcal A}_g}T_n(\operatorname{taut}(\alpha)) \Lambda \lambda_g.\\[-46pt] \end{align*} $$
Abelian subvarieties (and their dimensions) are preserved by isogenies, so Hecke operators preserve the
$\mathbb {Q}$
-span of these
$\operatorname {NL}$
-cycles. We focus on the
$\operatorname {NL}$
-cycles corresponding to elliptic subgroups.
Definition 6. Let
$$ \begin{align*}\mathbf{NL}_g \subset \mathsf{CH}^{g-1}(\mathcal A_g) \end{align*} $$
be the subspace generated by
$\lambda _{g-1}$
and all the
$\operatorname {NL}_{g,d}$
for
$d \geq 1$
. The NL-Hecke algebra is the subalgebra
$$ \begin{align*}\mathsf{Hecke}^{\operatorname{NL}}_g \subset \operatorname{End}_{\mathbb{Q}}(\mathbf{NL}_g) \end{align*} $$
generated by all the
$T_n$
.
Proposition 18. The NL-Hecke algebra has the following properties:
-
1.
$\mathsf {Hecke}^{\operatorname {NL}}_g$
is commutative, preserves the
$\mathbb {Q}$
-span of
$\lambda _{g-1}$
. -
2. As a
$\mathsf {Hecke}^{\operatorname {NL}}_g$
-module,
$\mathbf {NL}_g$
is generated by
$[\mathcal A_1 \times \mathcal A_{g-1}]$
and
$\lambda _{g-1}$
. -
3.
$\mathsf {Hecke}^{\operatorname {NL}}_g$
is generated by the
$T_p$
for p prime.
In particular, if
$[\mathcal A_1\times \mathcal A_{g-1}]$
is tautological, then
$\mathbf {NL}_g$
is
$1$
-dimensional.
Proof. The Hecke algebra of correspondences on
$\mathcal A_g$
is well-known to be commutative, see [Reference Chai and Faltings12, Chapter VII], and the rest of a) has been discussed before. For b), note that
$$ \begin{align*}\pi_2\left(\pi_1^{-1}(\mathcal A_1 \times \mathcal A_{g-1})\right) \end{align*} $$
is the set of principally polarized abelian varieties
$(Y, \theta _Y)$
having an isogeny
$f: E \times X' \longrightarrow Y$
, where
$X'$
is also principally polarized and
$f^*\theta _Y = n\theta _E + n\theta _{X'}$
. The induced map
$$ \begin{align*}g: E \longrightarrow E \times \{0\} \subset E \times X' \longrightarrow Y \end{align*} $$
satisfies that
$g^*\theta _Y = n \theta _E$
, and so
$g(E)$
is an elliptic subgroup of Y and
$\theta _{Y | g(E)}$
has degree
$n/|\ker (g)|$
.
Given Y with an elliptic subgroup F such that
$\theta _{Y|F}$
has degree
$m \mid n$
, let
$Y'$
be the complementary subvariety of F.
$\theta _{Y|Y'}$
is of type
$(1,\ldots , 1,m)$
, so in particular, there is a principally polarized
$X'$
and an isogeny
$X' \longrightarrow Y'$
such that the pullback of
$\theta _{Y'}$
is n times the polarization of
$X'$
. If
$E \longrightarrow F$
has degree
$n/m$
then
$X:= E \times X'$
maps to Y under the correspondence. Therefore,
$$ \begin{align*}\pi_2\left(\pi_1^{-1}(\mathcal A_1 \times \mathcal A_{g-1})\right) = \bigcup_{m \mid n}\operatorname{NL}_{g,m}, \end{align*} $$
and
$$ \begin{align*}T_n([\mathcal A_1 \times \mathcal A_{g-1}]) = \sum_{m \mid n}c_{n,m} [\operatorname{NL}_{g,m}]. \end{align*} $$
for some positive coefficients
$c_{n,m}$
. This proves b).
Any isogeny decomposes uniquely into isogenies of relatively prime degrees. Therefore,
$\mathsf {Hecke}_g^{\operatorname {NL}}$
is generated by all the
$T_{p^k}$
. By the same arguments that we explained before,
$$ \begin{align*}\pi_2\left(\pi_1^{-1}(\operatorname{NL}_{g,d})\right) = \bigcup_{m \mid nd}\operatorname{NL}_{g,m} \end{align*} $$
and so,
$$ \begin{align*}T_p(\stackrel{l \text{ times}}{\ldots} (T_p([\mathcal A_1 \times \mathcal A_{g-1}])\ldots ) = \sum_{i=0}^l d_{l,i} [\operatorname{NL}_{g,p^i}] \end{align*} $$
and
$$ \begin{align*}T_{p^k}([\mathcal A_1 \times \mathcal A_{g-1}]) = \sum_{i=0}^k e_{k,i} [\operatorname{NL}_{g,p^i}] \end{align*} $$
for some positive numbers
$d_{l,i}, e_{k,i}$
. Therefore, one solves a triangular system to find a polynomial
$q \in \mathbb {Q}[T]$
of degree k such that
$$ \begin{align*}(T_{p^k} - q(T_p)) ([\mathcal A_1 \times \mathcal A_{g-1}])=0. \end{align*} $$
By Lemma 17 the Hecke operators commute with
$\operatorname {taut}$
, and
$\operatorname {taut}([\mathcal A_1 \times \mathcal A_{g-1}])$
is a multiple of
$\lambda _{g-1}$
. Therefore,
$$ \begin{align*}(T_{p^k} - q(T_p)) (\lambda_{g-1}) =0. \end{align*} $$
Since the Hecke algebra is commutative, and
$\mathbf {NL}_g$
is generated by
$\lambda _{g-1}$
and
$[\mathcal A_1 \times \mathcal A_{g-1}]$
, this shows that the relation
$T_{p^k} = q(T_p)$
holds in
$\mathsf {Hecke}_g^{\operatorname {NL}}$
.
If
$[\mathcal A_1\times \mathcal A_{g-1}]$
is tautological, it must equal its tautological projection, so
$\mathbf {NL}_g$
would be generated by
$\lambda _{g-1}$
and the Hecke operators, but
$\lambda _{g-1}$
is a common eigenvector of them.
The space
$\operatorname {Mod}_{2g}$
of modular forms of weight
$2g$
for
$\operatorname {SL}_{2}(\mathbb Z)$
also has an action of a commutative Hecke algebra generated by elements
$T_p$
for primes p, and is generated by an Eisenstein form and a cusp form as a module over the Hecke algebra. Therefore, Proposition 18 supports Conjecture 1.
Proof of Theorem 2.
Note that
$\mathrm {Tor}^{-1}(\operatorname {NL}_{g,2}) \cap \mathcal M_g$
is precisely the bielliptic locus, which has the expected codimension
$g-1$
, so the image of
$[\operatorname {NL}_{g,2}]$
by the maps
$$ \begin{align*}\mathsf{CH}^{g-1}(\mathcal A_{g}) \stackrel{\operatorname{Tor}^*}{\longrightarrow} \mathsf{CH}^{g-1}(\mathcal M_g^{ct}) \longrightarrow \mathsf{CH}^{g-1}(\mathcal M_g) \end{align*} $$
is a positive multiple of the class of the bielliptic locus, which is not tautological by the work of [Reference Arena, Canning, Clader, Haburcak, Li, Chi Mok and Tamborini2] in the cases
$g=12$
and
$g \geq 16$
even. However, these maps send tautological classes to tautological classes. Therefore,
$\operatorname {NL}_{g,2}$
cannot be tautological and by Proposition 18,
$[\mathcal A_1\times \mathcal A_{g-1}]$
cannot be tautological either.
Remark 19. In fact, since
$\operatorname {Tor}^{-1}(\mathcal A_1 \times \mathcal A_{g-1}) \cap \mathcal M_g = \emptyset $
, we cannot write
$[\operatorname {NL}_{g,2}]$
in terms of
$[\mathcal A_1 \times \mathcal A_{g-1}]$
and
$\lambda _{g-1}$
. Therefore,
$\dim (\mathbf {NL}_g) \geq 3$
for
$g=12$
or
$g \geq 16$
even.
5 The homomorphism property
Recall from Definition 2 that
$(\alpha , \beta )$
has the homomorphism property if
$$ \begin{align*}\operatorname{taut}(\alpha \cdot \beta) = \operatorname{taut}(\alpha)\cdot \operatorname{taut}(\beta). \end{align*} $$
Proof of Theorem 6.
Note that
$$ \begin{align*}\lambda_{g-1}\mid_{\operatorname{NL}_{g, \delta}} =0. \end{align*} $$
This is because, after pulling back to
$\mathcal A_{u, g-u, \delta }$
,
${\mathbb E}_g$
splits as the sum of two vector bundles with vanishing top Chern class. In [Reference van der Geer38] it is explained that
$\mathsf {R}^*(\mathcal A_g)$
is additively generated over
$\mathbb {Q}$
by monomials
$\lambda _1 ^{u_1}\ldots \lambda _{g-1}^{u_{g-1}}$
with
$u_i \in \{0,1\}$
, so if
$\alpha \in \mathsf {CH}^*(\mathcal A_g)$
is a class such that
$\lambda _{g-1}\cdot \alpha = 0$
then
$\lambda _{g-1}\cdot \operatorname {taut}(\alpha ) = 0$
and so
$\lambda _{g-1} \mid \operatorname {taut}(\alpha )$
.
This shows that
$\lambda _{g-1} \mid \operatorname {taut}(\alpha )$
whenever
$\alpha $
is supported on an
$\operatorname {NL}$
cycle, so
$ 0 = \lambda _{g-1}^2 \mid \operatorname {taut}(\alpha ) \cdot \operatorname {taut}(\beta )$
whenever
$\alpha $
and
$\beta $
are supported on
$\operatorname {NL}$
cycles. Finally,
$\operatorname {taut}(\alpha \cdot \beta )$
was shown to be
$0$
in Proposition 13.
The homomorphism property is connected to the
$\lambda _g$
-pairing on
$\mathcal {M}_g^{ct}$
by the following, which is a generalization of the proof of [Reference Canning, Oprea and Pandharipande15, Theorem 5].
Proposition 20. Let
$k \leq 2g-3$
be a positive integer such that
$R^{2g-3-k}(\mathcal M_g)$
is generated by monomials in the
$\lambda _i$
Footnote
5
. If
$\alpha \in \mathsf {CH}^k(\mathcal A_g)$
and
$(\alpha , \beta )$
has the homomorphism property whenever
$\beta $
is supported on
$\mathcal A_u \times \mathcal A_{g-u}$
for all u, then the pair
$(\alpha , \operatorname {Tor}_*(\mathbf {1}))$
has the homomorphism property if and only if
$\operatorname {Tor}^*(\alpha - \operatorname {taut}(\alpha )) \in \mathsf {CH}^k(\mathcal M_g^{ct})$
lies in the kernel of the
$\lambda _g$
-pairing
$$ \begin{align*}\mathsf{CH}^k(\mathcal M_g^{ct}) \times \mathsf{R}^{2g-3-k}(\mathcal M_g^{ct}) \longrightarrow \mathsf{CH}^{2g-3}(\mathcal M_g^{ct}) \longrightarrow \mathbb{Q}. \end{align*} $$
Proof. We work on a toroidal compactification of
$\mathcal A_g$
such that the Torelli map extends to a proper morphism
$\overline {\operatorname {Tor}}$
defined on
$\overline {\mathcal M}_g$
; for example, the second Voronoi compactification works by [Reference Namikawa33], and the perfect cone compactification also works by [Reference Alexeev and Brunyate1]. By formula (1.5),
$$ \begin{align*}\operatorname{taut}(\alpha \cdot \operatorname{Tor}_*(\mathbf{1})) - \operatorname{taut}(\alpha) \cdot \operatorname{taut}(\operatorname{Tor}_*(\mathbf{1})) = \operatorname{taut}(\operatorname{Tor}_*(\mathbf{1})\cdot (\alpha -\operatorname{taut}(\alpha)). \end{align*} $$
This class is zero if and only if
$$ \begin{align*}\int_{\overline{\mathcal M}_g} (\overline{\operatorname{Tor}}^*(\overline{\alpha}) - \overline{\operatorname{Tor}}^*(\operatorname{taut}(\alpha)))\Lambda \lambda_g=0. \end{align*} $$
For any polynomial
$\Lambda $
on the
$\lambda _i$
. We are using that
$\overline {\operatorname {Tor}}^*(\overline {\alpha })$
is an extension of
$\operatorname {Tor}^*(\alpha )$
to
$\overline {\mathcal M}_g$
and that
$\overline {\operatorname {Tor}}^*$
preserves the Hodge bundle.
By the assumption on k, the rest of the classes in
$\mathsf {R}^{2g-3-k}(\mathcal M_{g}^{ct})$
are supported on the boundary
${\mathcal M^{ct}_g \smallsetminus \mathcal M_g}$
, but their pushforward under the Torelli map lies in
$\mathcal A_{u}\times \mathcal A_{g-u}$
for some u, so the homomorphism property holds for these pushforwards by Theorem 6.
6 Gromov-Witten theory of the universal elliptic curve
Definition 7. Let
$\pi : \overline {\mathcal E} \longrightarrow \overline {\mathcal M}_{1,1}$
be the universal curve, with section q. The
$\pi $
-relative moduli space of log-stable maps of degree d from genus g curves is denoted by
$$ \begin{align*}\overline{\mathcal M}_{g,1}(\pi, d). \end{align*} $$
Over a scheme S, it parametrizes the data of:
-
• a nodal curve
$C \longrightarrow S$
of genus g, with its canonical log structure (given by its singular locus), -
• a quasi-stableFootnote 6 curve
$E \longrightarrow S$
of arithmetic genus
$1$
with a section, and the canonical log structure given by its singular locus, -
• a log stable map
$f:C \longrightarrow E$
such that
$\operatorname {Aut}(f)$
is finite.
The log condition says that, if E is a singular elliptic curve, then the preimage by f of a node consists of nodes, and on an étale neighborhood of each node in the domain, the map is given by
$$ \begin{align*}\begin{array}{rcl} \frac{\mathbb{C}[x,y]}{xy=0} &\longrightarrow & \frac{\mathbb{C}[a,b]}{ab=0} \\ (x,y) & \mapsto & (a^k, b^k). \end{array} \end{align*} $$
This space comes with a virtual fundamental class of dimension
$$ \begin{align*}\mathrm{vdim}\left(\overline{\mathcal M}_{g,1}(E,d)\right) + \dim\left(\overline{\mathcal M}_{1,1}\right) =2g, \end{align*} $$
and natural morphisms
$$ \begin{align*}\mathsf{ev}:\overline{\mathcal M}_{g,1}(\pi, d) \longrightarrow \overline{\mathcal E}\text{ and }\mathsf{ft} :\overline{\mathcal M}_{g,1}(\pi, d) \longrightarrow \overline{\mathcal M}_{g,1}. \end{align*} $$
Let
$\mathcal M_{g,1}^{ct}(\pi ,d)$
be the inverse image of
$\mathcal M^{ct}_{g,1}$
under
$\mathsf {ft}$
, and
$\mathcal E$
be the universal elliptic curve over
$\mathcal M_{1,1}$
.
Lemma 21. If
$d>0$
, the map
$\mathsf {ev} : \mathcal M_{g,1}^{ct} (\pi ,d) \longrightarrow \overline {\mathcal E}$
factors through
$\mathcal E$
.
Proof. Let
$P = P_1 \cup \ldots \cup P_k$
be a cycle of k rational curves, with nodes
$n_1, \ldots , n_k$
. If
$f:C \longrightarrow P$
is a log-stable map and
$f(q) =n_i$
then q has to be a node. If
$C' \subset C$
is an irreducible component that is not contracted by f, we obtain a surjective map from
$C'$
to
$P_i$
for some i, so there are at least two points in
$C'$
mapped to some node. Therefore, f contracts all the irreducible components of C whose corresponding vertex in the dual graph is adjacent to only one edge. If C is of compact type, one can contract all the leaves of its dual graph repeatedly, and so f has to be constant, which is impossible because
$d>0$
.
Lemma 22.
$\mathsf {ft}^*(\psi _1)$
agrees with the
$\psi _1$
class on
$\mathcal {M}^{ct}_{g,1}(\pi , d)$
.
Proof. Indeed, by Lemma 21, every rational component of the domain of a stable map in
$\mathcal M_{g,1}^{ct}(\pi , d)$
maps to an elliptic curve, so it is contracted. Therefore the domain curve is always stable, so the two
$\psi $
classes are the same.
Note that for a pointed compact type curve
$(C, p)$
and an elliptic curve E,
$$ \begin{align} \left\lbrace \begin{array}{cc} \text{Homomorphisms }f : E \longrightarrow\operatorname{Jac}(C) \\ \text{such that}\deg (f^*(\theta_C))=d \end{array}\right\rbrace \longleftrightarrow \left\lbrace \begin{array}{cc} \text{Maps }h : (C,p) \longrightarrow(E,0) \\ \text{of degree }d \end{array}\right\rbrace. \end{align} $$
Indeed, given
$f:E \longrightarrow \operatorname {Jac}(C)$
and p, the map h is
$f^\vee \circ \operatorname {aj}_p$
, where
$$ \begin{align*}\operatorname{aj}_p : (C,p) \longrightarrow (\operatorname{Jac}(C), 0) \end{align*} $$
is the Abel-Jacobi map, and given h, f will be the dual of the map
$\operatorname {Jac}(C) \longrightarrow E$
given by the Albanese property of
$\operatorname {Jac}(C)$
.
We construct the moduli spaces of both sides of the equivalence (6.1). Let
$\mathcal {Q}_{g,d}$
be the fibered product
Consider the morphism
$$ \begin{align*}\operatorname{Tor}_1 \colon \mathcal M_{g,1}^{ct} \longrightarrow \mathcal A_g, \end{align*} $$
which is the composition of the Torelli morphism with the forgetful morphism. We define
$\operatorname {Tor}_1^{-1}(\widetilde {\operatorname {NL}}_{g,d})$
as the fibered product
where
$\widetilde {\operatorname {NL}}_{g,d}$
is the stack of maps
$E \longrightarrow X$
of degree d (and was already considered in 4). By (6.1), which clearly works in families, the following holds:
Lemma 23 (Generalizing [Reference Canning, Oprea and Pandharipande15], Proposition 21, see also [Reference Greer and Lian25]).
There is an isomorphism of stacks
$$ \begin{align*}\mathcal Q_{g,d} \longrightarrow \operatorname{Tor}_1^{-1}(\widetilde{\operatorname{NL}}_{g,d}). \end{align*} $$
over
$\mathcal M_{g,1}^{ct}$
.
Proof. The morphism
$\mathcal Q_{g,d} \longrightarrow \widetilde {\operatorname {NL}}_{g,d}$
is the one that we have described above using the Abel-Jacobi map. Together with
$\mathsf {ft}$
, this gives a natural morphism
$\mathcal Q_{g,d} \longrightarrow \operatorname {Tor}_1^{-1}(\widetilde {\operatorname {NL}}_{g,d})$
, and an inverse is constructed likewise, because the equivalence (6.1) works in families.
But moreover, there is an equality of virtual cycles:
Lemma 24 (See [Reference Greer and Lian25], Theorem 2).
Under the isomorphism in Lemma 23, there is an equality of cycles
$$ \begin{align*}\operatorname{Tor}_1^*([\widetilde{\operatorname{NL}}_d]) = q^!\left(\left[\mathcal M_{g,1}^{ct}(\pi,d)\right]^{\mathrm{vir}}\right). \end{align*} $$
In particular, there is a canonical extension of
$\operatorname {Tor}_1^*([\widetilde {\operatorname {NL}}_{g,d}])$
to
$\overline {\mathcal M}_{g,1}$
.
Proof of Theorem 7.
First note that
$[\operatorname {NL}_{g,d}]$
and
$[\widetilde {\operatorname {NL}}_{g,d}]$
are related by the invertible relation (3.1), so we may exchange them freely. Recall also that the tautological projection of
$\widetilde {\operatorname {NL}}_{g,d}$
was calculated in the proof of Corollary 4.
Since
$[\widetilde {\operatorname {NL}}_{g,d}]$
is a class of codimension
$g-1$
, has the homomorphism property with respect to any class supported on an
$\operatorname {NL}$
-cycle (6), and
$\mathsf {R}^{g-2}(\mathcal M_g)$
is generated by
$\lambda $
classes, we may apply 20, so
$[\widetilde {\operatorname {NL}}_{g,d}]$
and
$\operatorname {Tor}_*(1)$
have the homomorphism property if and only if
$$ \begin{align} \operatorname{Tor}^*\left([\widetilde{\operatorname{NL}}_{g,d}] - \frac{g\sigma_{2g-1}(d)}{6|B_{2g}|}\lambda_{g-1} \right) \end{align} $$
pairs to
$0$
with every tautological class on
$\mathcal M_g^{ct}$
. By Lemmas 24 and 22,
$$ \begin{align*}\frac{1}{2g-2}\pi_*\mathsf{ft}_*\left( q^!\psi_1\left[\overline{\mathcal M}_{g,1}(\pi,d)\right]^{\mathrm{vir}}\right) \end{align*} $$
is an extension of
$\operatorname {Tor}^*([\widetilde {\operatorname {NL}}_{g,d}])$
to
$\overline {\mathcal M}_g$
, where the
$\frac {1}{2g-2}$
factor comes from the insertion of the
$\psi $
class. In fact,
$\mathsf {R}^{g-2}(\mathcal M_g)$
is generated by
$\lambda _{g-2}$
by the work in [Reference Looijenga30], so (6.2) is in the kernel of the
$\lambda _g$
pairing if and only if
$$ \begin{align*}\frac{1}{2g-2} \int_{[\overline{\mathcal M}_{g,1}(\pi,d)]^{\mathrm{vir}}} \psi_1 \mathsf{ev}^*(q) \lambda_{g-2}\lambda_g = \frac{g\sigma_{2g-1}(d)}{6|B_{2g}|} \int_{\overline{\mathcal M}_g}\lambda_{g-2}\lambda_{g-1}\lambda_g = \frac{|B_{2g-2}|\sigma_{2g-1}(d)}{24(2g-2)(2g-2)!}, \end{align*} $$
where the last integral was computed in [Reference Faber and Pandharipande21]. This completes the proof.
7 Degree computations
We compute the degrees of the maps
$\phi _\delta $
and
$\pi _\delta $
and the volume of the Hecke operator
$T_n$
.
7.1 The degree of
$\phi _\delta $
We first consider the case
$\delta = (1,\ldots ,1, d, \ldots ,d)$
to illustrate the ideas that we will use.
7.1.1 The case
$\delta = (1, \ldots , 1,d,\ldots ,d)$
Throughout this part, k is the number of
$1$
entries and h is the number of d entries, so
$h +k=g$
.
Proposition 25. When
$\delta = (\underbrace {1, \ldots ,1}_{k \text { times}},\underbrace {d, \ldots ,d}_{h \text { times}})$
, the degree of
$\phi _\delta $
is
$$ \begin{align*}d^{h(2g+1)} \prod_{p \mid d}\prod_{i=g-h+1}^{g}(1-p^{-2i}), \end{align*} $$
where the product is over all primes dividing d.
By Lemma 9, this is the same as the index of the subgroup of
$\operatorname {Sp}_{2g}(\mathbb {Z})$
consisting of matrices that can be written as
where the
$a_{ij}, b_{ij}, c_{ij}, e_{ij}$
are integers.
For an integer n and a prime p,
$v_p(n)$
denotes the highest power of p that divides n. If we write
$d = p_1^{v_{p_1}(d)}\cdot \ldots \cdot p_m^{v_{p_m}(d)}$
, and
$\delta _i = (1,\ldots ,1, p_i^{v_{p_i}(d)}, \ldots , p_i^{v_{p_i}(d)})$
then
$$ \begin{align} \Gamma_{g}[\delta] = \bigcap_{i=1}^m \Gamma_{g}[\delta_i], \end{align} $$
and so we can reduce to the case where
$d=p^v$
.
We are going to stratify
$\mathrm G_\delta [\delta ]$
by intersecting it with the normal subgroups
$$ \begin{align*}\Gamma_g[p^i] = \operatorname{Sp}_{2g}(\mathbb{Z})[p^i] = \ker \left(\operatorname{Sp}_{2g}( \mathbb{Z}) \longrightarrow\operatorname{Sp}_{2g}(\mathbb{Z}/p^i\mathbb{Z})\right), \end{align*} $$
and since
$\Gamma _g[d^{2v}] \leq \mathrm G_\delta [\delta ]$
,
$$ \begin{align*}[\operatorname{Sp}_{2g} (\mathbb{Z}) : \mathrm G_\delta[\delta]] \cdot \prod_{i=1}^{2v}\left|\mathrm{im}\left(\mathrm G_\delta[\delta] \cap \Gamma_g[p^{i-1}] \longrightarrow\operatorname{Sp}_{2g}( \mathbb Z/p^i\mathbb{Z})\right)\right| = \left|\operatorname{Sp}_{2g}( \mathbb{Z}/p^{2v}\mathbb{Z}) \right|. \end{align*} $$
After stratifying
$\Gamma _{g}[p^{2v}]$
in the same way, one arrives at the equality
$$ \begin{align} [\operatorname{Sp}_{2g}(\mathbb{Z}) : \mathrm G_\delta[\delta]] =\prod_{i=1}^{2v}\frac{\left|\mathrm{im}\left(\Gamma_{g}[p^{i-1}] \longrightarrow\operatorname{Sp}_{2g}(\mathbb{Z}/p^{i}\mathbb{Z})\right)\right|}{\left|\mathrm{im}\left(\mathrm G_\delta[\delta] \cap \Gamma_g[p^{i-1}] \longrightarrow\operatorname{Sp}_{2g}(\mathbb Z/p^i\mathbb{Z})\right)\right|} \end{align} $$
The
$i=0$
computation is different, so we do this first. By a Gram-Schmidt procedure, any linearly independent set of vectors that spans an isotropic subspace of
$\mathbb F_p^{2g}$
can be extended to a symplectic basis. In other words,
$\operatorname {Sp}_{2g}(\mathbb F_p)$
acts transitively on the set
$$ \begin{align*}\{(e_1, \ldots , e_h) \in \mathbb (\mathbb F_p^{2g})^h: \langle e_1, \ldots , e_h\rangle \text{ is an }h\text{-dimensional isotropic subspace}\}, \end{align*} $$
which has cardinality
$$ \begin{align*}(p^{2g}-1)(p^{2g-1}-p)\ldots (p^{2g-(h-1)}-p^{h-1}) = p^{2gh-\binom{h}{2}} \prod_{i=g-h+1}^g(1-p^{-2i}) \end{align*} $$
From (7.1), we see that
$$ \begin{align*}\mathrm{im}\left(\mathrm G_\delta[\delta] \longrightarrow\operatorname{Sp}_{2g}(\mathbb F_p)\right) \end{align*} $$
is the same as the set of symplectic endomorphisms
$\mathbb F_p^{2g} \longrightarrow \mathbb F_p^{2g}$
that leave fixed the last h vectors of the standard symplectic basis; in other words, it is the stabilizer of a point for the above action, and so
$$ \begin{align*}\frac{|\operatorname{Sp}_{2g}( \mathbb F_p)|}{\left|\mathrm{im}\left(\mathrm G_\delta[\delta] \longrightarrow\operatorname{Sp}_{2g}( \mathbb F_p)\right)\right|} = p^{2gh-\binom{h}{2}}\prod_{i=g-h+1}^g(1-p^{-2i}). \end{align*} $$
For
$i>1$
, an element of
$\mathrm {im}\left (\Gamma _g[p^{i-1}] \longrightarrow \operatorname {Sp}_{2g}( \mathbb {Z}/p^i\mathbb {Z})\right )$
can be uniquely written as
where
$A,B,C,D$
have entries in
$\mathbb F_p$
, and
$B,C$
are symmetric. If we write
$$ \begin{align*}A = \begin{pmatrix} A_1\\ A_2 \end{pmatrix}, \quad B = \begin{pmatrix} B_1&B_2\\ B_2^t&B_4 \end{pmatrix}, \end{align*} $$
where
$A_1\in \mathrm {M}_{k\times g}(\mathbb F_p)$
,
$A_2\in \mathrm {M}_{h\times g}(\mathbb F_p)$
,
$B_1\in \operatorname {Sym}_{k\times k}(\mathbb F_p)$
,
$B_2\in \mathrm {M}_{k\times h}(\mathbb F_p)$
,
$B_4\in \operatorname {Sym}_{h\times h}(\mathbb F_p)$
. After inspecting (7.1) we arrive at the following:
-
• If
$1<i\leq v$
then M is in
$\mathrm {im}\left (\mathrm G_\delta [\delta ]\cap \Gamma _g[p^{i-1}] \longrightarrow \operatorname {Sp}(2g, \mathbb {Z}/p^i)\right )$
if and only if
$A_2=B_2=B_4=0$
over
$\mathbb F_p$
. -
• If
$v<i\leq 2v$
then M is in
$\mathrm {im}\left (\mathrm G_\delta [\delta ]\cap \Gamma _g[p^{i-1}] \longrightarrow \operatorname {Sp}(2g, \mathbb {Z}/p^i)\right )$
if and only if
$B_4=0$
over
$\mathbb F_p$
.
Therefore
$$ \begin{align*}\frac{\left|\mathrm{im}\left(\Gamma_{g}[p^{i-1}] \longrightarrow\operatorname{Sp}(2g, \mathbb{Z}/p^{i}\mathbb{Z})\right)\right|}{\left|\mathrm{im}\left(\mathrm G_\delta[\delta] \cap \Gamma_g[p^{i-1}] \longrightarrow\operatorname{Sp}(2g, \mathbb Z/p^i\mathbb{Z})\right)\right|} = \begin{cases} p^{hg + hk + h(h+1)/2} &\text{if }1<i\leq v\\ p^{h(h+1)/2}&\text{if }v<i\leq 2v \end{cases}, \end{align*} $$
and this proves Proposition 25, since the sum of all the powers of p that appear is
$$ \begin{align*}p^{2gh-\binom{h}{2} + (v-1)(hg + hk + h(h+1)/2) + (2v-v)(h(h+1)/2)} = p^{vh(2g+1)}. \end{align*} $$
7.1.2 The general case
For a general sequence
$\delta $
, by (7.2) we can assume that
$\delta =(1,\ldots , 1, p^{v_1}, \ldots , p^{v_h})$
is formed by powers of a fixed prime p, with
$1\leq v_1\leq \ldots \leq v_h$
. The formula (7.3) is unchanged, with
$l=v_h$
. The
$i=1$
factor of the right hand side of (7.3) is again
$$ \begin{align*}p^{2gh-\binom{h}{2}}\prod_{i=g-h+1}^g(1-p^{-2i}), \end{align*} $$
and the rest of the factors can be obtained by stratifying. Note that on the i-th step of the computation of the stratification, we are looking at matrices of the form (7.4), its contribution to the product (7.3) is
$p^{N(i)}$
where
$N(i)$
is the number of entries
$a_{ij}'$
(for any
$i,j$
) or
$b_{ij}'$
(for
$i \leq j$
) of a matrix
$$ \begin{align*}M' = \left(\begin{array}{c|c} (a_{ij}') & (b_{ij}') \\ \hline (c_{ij}') & (e_{ij}') \end{array}\right) \end{align*} $$
of the form (7.1) (with
$\delta = (1,\ldots , 1, p^{v_1}, \ldots , p^{v_h})$
) that are always divisible by
$p^i$
. A simple computation shows that
$$ \begin{align*}\sum_{i=1}^{2v_h} N(i) = (v_1 + v_2+\ldots + v_h) (2g-h) + \sum_{i \leq j} (v_i +v_j) = (2g+1)(v_1 + \ldots + v_h), \end{align*} $$
and
$N(1) = h(2g-h) + h(h+1)/2 = 2gh - h(h-1)/2$
. Therefore,
$$ \begin{align*} [\operatorname{Sp}_{2g}(\mathbb{Z}) : \mathrm G_\delta[\delta]] &= \left(p^{2gh-\binom{h}{2}}\prod_{i =g-h+1}^g(1-p^{-2i})\right) p ^{N(2) + \ldots + N(2v_h)}\\ &= p^{(2g+1)(\sum_j v_j) } \prod_{i=g-h+1}^g(1-p^{-2i}). \end{align*} $$
This shows that:
Proposition 26. If
$\delta = (d_1, \ldots , d_g)$
is a polarization type with
$d=d_1\ldots d_g$
, denote by
$$ \begin{align*}h_p(\delta) = g-\max\{i : v_p(d_i)=0\}. \end{align*} $$
Then, the degree of
$\phi _\delta $
is
$$ \begin{align*}d^{2g+1} \prod_{p \mid d} \prod_{i=g-h_p(\delta)+1}^{g}(1-p^{-2i}) = d^{2g+1} \prod_{j =1}^g\prod_{p \mid d_j}(1-p^{-2j}). \end{align*} $$
7.2 The degree of
$\pi _\delta $
As an application, the degree of
$\pi _\delta $
(or equivalently, the cardinality of
$\operatorname {Sp}(K(\delta ))$
) is computed:
Proposition 27. If
$\delta = (d_1, \ldots , d_g)$
is a polarization type then
$$ \begin{align*}\deg (\pi_\delta) = \deg(\phi_\delta) \cdot d_1^{2g-2}d_2^{2g-6}\ldots d_g^{-2g+2}\prod_{1\leq i<j\leq g} \prod_{p \mid d_j/d_i}\frac{(1-p^{-2(j-i)})}{(1-p^{-2(j-i+1)})}, \end{align*} $$
where the product is over primes p.
Proof. We will compute this degree by means of the following formulas:
-
• If
$\delta = (1, d_2, \ldots , d_g)$
and
$\delta _1 = (d_2, \ldots , d_g)$
then
$\deg (\pi _\delta )=\deg (\pi _{\delta _1})$
. -
• If
$\delta = (d_1, \ldots , d_g)$
and
$\delta _2=(1, d_2/d_1, \ldots , d_g/d_1)$
then
$$ \begin{align*}\frac{\deg(\pi_\delta)}{\deg (\pi_{\delta_2})} = \frac{\deg(\phi_\delta)}{\deg (\phi_{\delta_2})}. \end{align*} $$
The first one follows because the fiber of
$\pi _{g,\delta }$
over
$(X, \theta )$
is the set of symplectic basis for
$\ker (\theta ) \cong (\mathbb {Z}^g/\delta \mathbb {Z}^g)^2$
, and clearly
$(\mathbb {Z}^g/\delta \mathbb {Z}^g)^2 \cong (\mathbb {Z}^g/\delta _1\mathbb {Z}^g)^2$
. The second one follows from the Hirzebruch-Mumford Proportionality theorem and the isomorphism
$$ \begin{align*}\mathcal A_{g, \delta_2} \cong \mathcal A_{g,d_1 \cdot \delta_2} = \mathcal A_{g,\delta}. \end{align*} $$
Using these formulas recursively, and noting that when
$\delta = (1,\ldots , 1)$
the degrees of
$\phi $
and
$\pi $
are both
$1$
, we arrive at the following:
$$ \begin{align*}\deg (\pi_\delta) = \deg (\phi_{\delta})\cdot \prod_{i=1}^{g-1} \frac{\deg (\phi_{(d_{i+1}/d_i, \ldots , d_g/d_i})}{\deg (\phi_{(1, d_{i+1}/d_i, \ldots , d_g/d_i)})}. \end{align*} $$
By Proposition 26,
$$ \begin{align*}\frac{\deg (\phi_{(d_{i+1}/d_i, \ldots , d_g/d_i})}{\deg (\phi_{(1, d_{i+1}/d_i, \ldots , d_g/d_i)})} = \left(\frac{d_i^{g-i}}{d_{i+1}\cdot \ldots \cdot d_g}\right)^2\cdot \prod_{j=1}^{g-i}\prod_{p \big| \frac{d_{j+i}}{d_i}}\frac{(1-p^{-2j})}{(1-p^{-2j-2})}.\\[-55pt] \end{align*} $$
7.3 The volume of
$T_n$
We compute the volume of
$T_n$
using ideas of [Reference Debarre17, Reference Bryan, Oberdieck, Pandharipande and Yin7]
Proposition 28. The volume of the Hecke correspondence
$T_n$
is given by
$$ \begin{align*}\prod_{p \mid n}\prod_{i=1}^g\frac{1-p^{g(v_p(n)+i)}}{1-p^{gi}}, \end{align*} $$
where the product is over primes.
Proof. Recall that
$T_n$
is defined by a correspondence
where both maps are étale. In particular,
$\operatorname {vol}(T_n)$
equals
$\deg (\pi _1)$
. For a principally polarized abelian variety
$(X,\theta _X)$
, the preimages
$\pi _1^{-1}[(X, \theta )]$
correspond to isogenies
$(X, \theta _X) \longrightarrow (Y, \theta _Y)$
such that
$f^* \theta _Y = n \theta _X$
.
The polarization
$\theta _X$
induces a Weil pairing on the n-torsion points of X, and agrees with the pairing that
$n\theta $
induces on
$\ker (n\theta ) = X[n]$
. Writing
$ \mathbb Z^g /n \mathbb Z^g =\mathbf Z/n$
, and
$\widehat {H} = \operatorname {Hom}(H, \mathbb C^*)$
, it is known that the Weil pairing can be seen as the canonical map
$$ \begin{align*} e :(\mathbf Z/n\times \widehat{\mathbf Z/n}) \times (\mathbf Z/n\times \widehat{\mathbf Z/n}) &\longrightarrow \mathbb C^*\\(x,\widehat{x}) , (y, \widehat{y}) & \mapsto \ \ \widehat{y}(x)\widehat{x}(y)^{-1} \end{align*} $$
By [Reference Birkenhake and Lange5, Corollary 2.4.4],
$\deg (\pi _1)$
agrees with the number of maximal isotropic subgroups
$K \subseteq X[n]$
. Lemma 29 below, which is due to Debarre [Reference Debarre17, proof of Proposition 2.1] and is stated in [Reference Bryan, Oberdieck, Pandharipande and Yin7, Lemma 1], gives a precise description of such subgroups.
Suppose that
$H = \mathbb Z/d_1\mathbb Z \times \ldots \times \mathbb Z/d_g \mathbb Z$
where
$d_i$
divides
$d_{i+1}$
. A homomoprhism
$$ \begin{align*}\mathbb Z^g \longrightarrow H \end{align*} $$
factors through
$n \mathbb Z^g$
if and only if
$d_g$
divides n. This homomorphism is given by a matrix in
$M_{g \times g}(\mathbb Z)$
, which can be uniquely put in Hermite normal form. This is given uniquely by a matrix
$(a_{ij})$
, where
$1 \leq a_{ij} \leq a_{jj}$
for
$i <j$
,
$a_{ij}=0$
for
$i>j$
and
$a_{ii} = d_i$
. There are
$$ \begin{align*}d_2 d_3^2 \ldots d_g^{g-1} \end{align*} $$
such matrices.
The number of symmetric homomorphisms
$u : H \longrightarrow \widehat {H}$
is counted by symmetric matrices, and the total number is
$$ \begin{align*}d_1^gd_{2}^{g-1} \ldots d_g. \end{align*} $$
Putting all of this together, we see that
$$ \begin{align*}\deg(\pi_1) = \sum_{\substack{(d_1, \ldots , d_g)\text{ such that}\\ d_1 \mid d_2 \mid \ldots \mid d_g \mid n}}(d_1 \ldots d_g)^{g}. \end{align*} $$
If
$n = p^k$
, the number agrees with
$$ \begin{align*}\sum_{l \geq 0} p^{lg}\mathcal P(l,k, g), \end{align*} $$
where
$\mathcal P(l,k,g)$
is the number of partitions of l into at most g parts, each of which is bounded by k. It is well-known that
$$ \begin{align*}\sum_{l \geq 0} \mathcal P(l,k,g) q^l = \prod_{i=1}^g\frac{1-q^{k+i}}{1-q^i}. \end{align*} $$
After the substitution
$q = p^g$
we obtain the expected result when n is a prime power, and in general it follows by decomposing n into prime powers.
Lemma 29. Given a quotient
$\mathbf Z/n \longrightarrow H$
and a symmetric homomorphism
$u : H \longrightarrow \widehat {H}$
then
$$ \begin{align*}K_u = \{(x, \widehat{x}) \in \mathbf Z/n \times H^* : u (x + H) = \widehat{x} \} \end{align*} $$
is a maximal isotropic subgroup of
$\mathbf Z/n \times \widehat {\mathbf Z/n}$
, and all maximal isotropic subgroups have this form.
Acknowledgements
I would like to thank Rahul Pandharipande for his patience, for proposing me this area of research and for all his support and guidance during the years of preparation of this article. I am very grateful to Gerard van der Geer for sharing his wisdom on the whole topic of moduli spaces of abelian varieties and for suggesting to look at Hecke operators. I would also like to thank Younghan Bae, Samir Canning, Alessio Cela, Lycka Drakengren, Jeremy Feusi, Samouil Molcho, and Johannes Schmitt for the many conversations at ETH Zürich about abelian varieties, curves and intersection theory, and for comments on drafts of this paper, and the anonymous referee for the constructive comments and improvements. I am grateful to Qizheng Yin for his remarks on how to compute volumes of Hecke operators. Carl Lian and François Greer have been very helpful in explaining their work and conjectures.
Competing interest
The author has no conflicts of interest to declare.
Funding statement
The author was supported by ERC-2017-AdG-786580-MACI and SNF-200020-219369.
Open access
