2. Current theory describing turbulent flow over forested hills

Current analytic theory of turbulent shear flow over low hills (e.g. Jackson & Hunt Reference Jackson and Hunt1975; Hunt et al. Reference Hunt, Leibovich and Richards1988; Belcher et al. Reference Belcher, Newley and Hunt1993) has provided an enduring and consistent framework for analysis and understanding of flow over low hills and even over steeper hills upwind of the separation region. The theory divides the flow into different layers, where the perturbations to the mean flow caused by the hill are governed by distinctly different dynamics. Separate solutions to the flow equations are found for each layer and then these are matched asymptotically between the layers. For hills of sufficiently low-slope to ignore flow separation, Hunt et al. (Reference Hunt, Leibovich and Richards1988) defined two main regions: (i) the outer region, where the response to the pressure field generated by flow over the hill is inviscid, and (ii) the inner region, where perturbations to the turbulent Reynolds stresses affect the perturbations to the mean flow. Each of these regions was further divided into two layers. The middle layer, of depth $h_m$ , is the lower part of the outer region through which flow responses are inviscid but rotational to accommodate shear in the approach flow. In the upper layer, extending from $h_m$ to the top of the boundary layer, flow responses are irrotational and can be computed by potential theory. The inner region consists of the shear stress layer of depth $h_i$ , and the thin inner surface layer, of depth $l_s$ , which allows formal matching with a surface boundary condition.

Finnigan & Belcher (Reference Finnigan and Belcher2004) extended the analytic theory of Hunt et al. (Reference Hunt, Leibovich and Richards1988) to hills covered by tall plant canopies by replacing the thin inner surface layer by a deep plant canopy parameterized by linearized flow equations in the upper canopy but where the unavoidably nonlinear dynamics in the lower canopy were treated heuristically. Harman & Finnigan (Reference Harman and Finnigan2009, Reference Harman and Finnigan2013) further developed Finnigan & Belcher (Reference Finnigan and Belcher2004) to accommodate more realistic 2D hills, and then Harman & Finnigan (Reference Harman and Finnigan2021) extended the theory to 3D hills.

In all of these small perturbation theories, whether over hills covered by a rough surface or a tall canopy, identifying the depths of the inner shear stress layer, $h_i$ , and the middle layer, $h_m$ , is critical to applying the theory. To derive the formula for $h_m$ , Hunt et al. (Reference Hunt, Leibovich and Richards1988) assumed that the flow approaching the hill could be described by a logarithmic profile in equilibrium with the upstream surface while in the inner shear stress layer $h_i$ , the interdependence of the perturbations to the turbulent shear stresses and the perturbations to the mean shear are assumed to obey the same mixing length flux-gradient relationship as in an equilibrium log law. Finnigan & Belcher (Reference Finnigan and Belcher2004) relies on the same formulae for $h_m$ and $h_i$ as Hunt et al. (Reference Hunt, Leibovich and Richards1988).

The formulae for $h_m$ and $h_i$ assume the flow over the hill remains attached (i.e. no flow separation). Over steeper 2D hills and over 3D hills, this assumption breaks down. If the flow separates, streamlines that were following the surface contour upwind leave the surface and delineate the boundary of a separation bubble. Downwind of the separation point the scale of the largest turbulent eddies increases abruptly. In the attached flow the largest eddies are limited by the local distance to the surface but after separation the largest eddies span the bubble depth, which is typically ${ {O}}(H)$ with $H$ representing the hill height. While the streamlines approaching a 3D hill in its plane of lateral symmetry go over the hill-centreline, streamlines to either side are deflected forming space curves whose principal normals intersect the hill surface at right angles (Finnigan Reference Finnigan2024).

As fluid parcels above the canopy advect over the hill, changes to the Reynolds stresses reflect the competing effects of two processes. First, the existing eddies are stretched and rotated by the mean flow as they follow the mean streamlines. Second, nonlinear interactions between the eddies will tend to equalize $T\!K\!E$ between their orthogonal components $u^{\prime}$ , $v^{\prime}$ and $w^{\prime}$ , and to transfer TKE to finer scale eddies where it is ultimately dissipated to heat through the action of viscosity. These effects are represented formally in the conservation equations for the turbulent normal and shear stresses, $\langle u'^2 \rangle$ , $\langle v'^2 \rangle$ , $\langle w'^2 \rangle$ , $\langle u'w' \rangle$ , $\langle v'w' \rangle$ and $T\!K\!E$ , where $T\!K\!E = (\langle u'^2 \rangle + \langle v'^2 \rangle + \langle w'^2 \rangle )/2$ . In these equations, the so-called production terms describe the transfer of kinetic energy from the mean flow to the larger energy-containing eddies of the turbulence while the turbulent diffusion and pressure-strain terms describe the nonlinear interactions between these eddies, which break them down and destroy their coherence. These nonlinear interactions determine $\tau$ , the time over which the large eddies remain coherent enough to receive energy directly from the mean flow. Here $\tau$ can be taken as $\tau \sim T\!K\!E/\epsilon$ , where $\epsilon$ is the rate of viscous dissipation of TKE. This definition is strictly only applicable to equilibrium situations, where the rate of viscous dissipation is in balance with the transfer of kinetic energy from the mean flow to the turbulence, but we will assume that is also indicative of the rate at which these large eddies lose their coherence as they interact with each other during their passage over the hill.

In regions where the time scale of hill-induced changes in the mean flow is small compared with $\tau$ (i.e. in the so-called rapid distortion regimes), the turbulent stresses will reflect their recent history of straining and rotation by the mean flow and Hunt et al. (Reference Hunt, Leibovich and Richards1988) assumes that this will be the case in the outer region in general and in the middle layer in particular. In regions where mean flow changes are slow compared with $\tau$ , the turbulence will approach a state of local equilibrium between the rate of straining by the mean flow and the resulting Reynolds stresses so that their relationship can be described by an eddy viscosity. Current theory assumes that we should observe this behaviour in the inner shear stress layer, $z \lt h_i$ .

Beneath the inner layer and above the ground surface lies the canopy layer, which introduces additional length scales ( $L_c$ and $h_c$ ), through the addition of canopy drag and the no-slip condition at the surface. In the canopy, turbulent stresses are complicated by wake production, $W_p$ , i.e. the production of turbulent eddies at scales defined by the canopy elements and associated short-circuiting of the inertial energy cascade (Finnigan Reference Finnigan2000; Shaw & Patton Reference Shaw and Patton2003). In addition, viscous dissipation increases by the work performed by the turbulence against the viscous drag of the canopy elements (Ayotte, Finnigan & Raupach Reference Ayotte, Finnigan and Raupach1999; Shaw & Patton Reference Shaw and Patton2003). For dense canopies ( $h_c/L_c \gt 1$ ), canopy drag eliminates the importance for the flow dynamics of shear stress at the underlying surface but at the same time ensures strong vertical gradients in turbulent stresses. Finally, behind the hill crest, the strong adverse pressure gradient can cause reversed flow and separation, which introduces the hill height $H$ as an additional length scale affecting the turbulence.

3. Simulation description and configuration

Numerical models of turbulent flow over forested hills take many forms that each provide value with varying levels of accuracy and cost (see recent review by Finnigan et al. (Reference Finnigan, Ayotte, Harman, Katul, Oldroyd, Patton, Poggi, Ross and Taylor2020)). Analytical models provide extremely timely solutions, but typically linearize the nonlinear equations that describe turbulent flow (e.g. Finnigan & Belcher Reference Finnigan and Belcher2004; Poggi et al. Reference Poggi, Katul, Finnigan and Belcher2008; Harman & Finnigan Reference Harman and Finnigan2009, Reference Harman and Finnigan2013). Reynolds-averaged Navier–Stokes models solve the full nonlinear equations but averaged over space and time such that the influence of turbulence is fully parameterized (e.g. Wilson et al. Reference Wilson, Finnigan and Raupach1998; Katul & Chang Reference Katul and Chang1999; Ross & Vosper Reference Ross and Vosper2005, among others). Similar to Reynolds-averaged Navier–Stokes, LES also solves the full nonlinear equations but relies on relatively isotropic grids and only spatially averages (or filters) the equations at scales smaller than the grid resolution, such that the largest scales of turbulence (i.e. those performing most of the transport) are resolved by the grid and only the smallest scales of turbulence (which primarily act to dissipate energy) must be parameterized (e.g. Moeng & Sullivan Reference Moeng and Sullivan2015). Although it is computationally expensive, LES has become a close counterpart to field and laboratory experiments over the past 30 plus years because of its ability to accurately simulate the time-evolving and spatially evolving response of turbulence to varying forcing over complex surfaces (e.g. Wood Reference Wood2000; Patton & Katul Reference Patton and Katul2009; Sullivan, McWilliams & Patton Reference Sullivan, McWilliams and Patton2014; Chamecki et al. Reference Chamecki, Freire, Dias, Chen, Dias-Junior, Toledo Machado, Sörgel, Tsokankunku and de Araújo2020).

In our LES, the governing equations describe 3D time-dependent turbulent winds in a dry incompressible Boussinesq atmospheric boundary layer, including (i) three transport equations for momentum $\rho {\boldsymbol{u}}$ , (ii) a transport equation for a conserved scalar variable, (iii) a discrete Poisson equation for a pressure variable $p$ to enforce incompressibility and (iv) closure expressions for subgrid-scale (SGS) variables, e.g. an equation for SGS TKE $e$ (see Sullivan et al. Reference Sullivan, McWilliams and Patton2014). The physical processes included in the LES boundary-layer equations include, temporal time tendencies, advection, pressure gradients, divergence of SGS fluxes, buoyancy, resolved turbulence, and in the case of the SGS $e$ equation also diffusion and dissipation.

Explicit spatial filtering of the momentum equations in the presence of vegetative-canopy elements generates terms representing canopy-induced pressure and viscous drag (Finnigan & Shaw Reference Finnigan and Shaw2008) which are parameterized using a time-dependent and local velocity-squared type drag law, e.g.

(3.1) \begin{equation} F_c = -\, c_d\,a\,|\boldsymbol{u}|\,\boldsymbol{u}, \end{equation}

where, $a$ is the canopy’s frontal area density and $c_d$ is a drag coefficient describing the canopy’s efficiency at absorbing momentum. Dissipation in the SGS energy equation is also augmented by the work SGS motions perform against the canopy-induced form drag. See Shaw & Patton (Reference Shaw and Patton2003), Patton & Katul (Reference Patton and Katul2009) and Patton et al. (Reference Patton, Sullivan, Shaw, Finnigan and Weil2016) for further details of the canopy representation in the LES.

By applying a transformation to the physical space coordinates $(x,y,z)$ that maps them onto flat computational coordinates $(\xi ,\eta ,\zeta )$ , Sullivan et al. (Reference Sullivan, McWilliams and Patton2014) adapted our flat LES (Sullivan & Patton Reference Sullivan and Patton2011) to a situation with a 3D time-evolving lower boundary shape $h = h(x,y,t)$ . The current simulations use this same framework, but impose a time-independent surface, e.g. $h = h(x,y)$ where the maximum hill slope $s_m = \text {max}( {\partial h}/{\partial x})$ . Of importance is that we transform the coordinates, not the flow variables. Therefore, horizontal velocity components ( $u$ , $v$ ) are defined in a right-handed Cartesian coordinate system parallel to the flat surface surrounding each hill (with $u$ aligned with the imposed pressure gradient force in the $+x$ direction, and $v$ positive to the left of the imposed pressure gradient force in the $+y$ direction), and vertical velocity ( $w$ ) is defined positive upward from the underlying flat surface (the $+z$ direction) aligned opposite to the gravitational force (although the flow under consideration is neutrally stratified, so gravitational forces are ignored).

The simulations discretize a 4096 $\times$ 2048 $\times$ 512 m $^3$ domain using 2048 $\times$ 1024 $\times$ 256 grid points. The computational mesh in physical space is surface following and non-orthogonal. Vertical grid lines are held fixed at a particular $(x,y)$ location but the horizontal grid lines undergo vertical translation according to the vertical variation of the underlying surface. While the grid resolution in the horizontal directions is fixed for all horizontal locations, the vertical grid is refined near the surface to resolve near-surface/canopy processes and is then algebraically stretched above the canopy to push the upper boundary far above the hill to minimize any influence of the upper boundary on the hill-induced pressure field. Care is taken to ensure that every grid volume uses an aspect ratio no larger than $5:1$ attempting to reasonably satisfy isotropy assumptions used to close the equations in the SGS model.

Figure 2.

Example of the horizontal domains used and the idealized cosine-shaped 2D and 3D hills. Panel (b) reflects the axisymmetric case with $L = L_y = L_x$ . The blue line spanning the domain at $x$ = 1024 m depicts the downwind boundary of the horizontally homogeneous periodic region, while the green line spanning the domain at $x \sim$ 3892 m depicts the beginning of the fringe region where the solutions begin to be nudged back to those at the downwind edge of the upwind periodic region starting at the green line located at $x \sim$ 820 m. Periodic boundary conditions are imposed in the $y$ -direction. The vertical domain extends up to 512 m.

Spatial differencing is pseudospectral in the horizontal computational directions $(\xi , \eta )$ and is second-order finite difference in $\zeta$ . Time stepping uses a low-storage third-order Runge–Kutta scheme, and the time step $\delta t$ is picked dynamically based on a fixed Courant–Fredrichs–Lewy number.

An important development for this effort involves implementing a turbulent inflow fringe (or precursor) method which is compatible with our pseudospectral spatial differencing and third-order Runge–Kutta time differencing (Schlatter, Adams & Kleiser Reference Schlatter, Adams and Kleiser2005; Munters, Meneveau & Meyers Reference Munters, Meneveau and Meyers2016) to enable simulation of flow over isolated 2D and 3D hills. The strategy involves simulating two interconnected periodic domains, where the flow in the upwind domain is periodic and representative of flow over an infinitely long horizontally homogeneous forested surface. The outflow of that upwind domain serves as inflow for the downwind domain containing the hill. In the second domain at the boundary far downstream from the hill, nudging terms are applied over the downwind-most 102 grid points (from grid points 1946–2048) to force the exit flow of the larger downwind domain to match the flow exiting the upstream region (note that 102 grid points is 20 % of the upwind domain). Hence both domains use periodic boundary conditions in the $x$ direction, but the flow impinging on the hill is unaware of any upstream hills. It is important to note two things: (i) the size of the upstream inflow domain dictates the largest scales of motion impinging on the hill located in the downstream domain, and (ii) the chosen fringe strategy used in these simulations was developed prior to and differs from the two-domain strategy discussed in Sullivan et al. (Reference Sullivan, McWilliams, Weil, Patton and Fernando2020, Reference Sullivan, McWilliams, Weil, Patton and Fernando2021) that ensures decoupling of inflow conditions from any slight imperfections in the spectral tapering (e.g. Inoue, Matheou & Teixeira Reference Inoue, Matheou and Teixeira2014) and which enables inclusion of Coriolis and buoyancy forces. (For these reasons, we recommend using the technique described by Sullivan et al. (Reference Sullivan, McWilliams, Weil, Patton and Fernando2020, Reference Sullivan, McWilliams, Weil, Patton and Fernando2021) for future studies.) Figure 2 shows the total extent of the horizontal domain for the two steeper hill configurations ( $s_m =$ 0.26). The blue lines in figure 2 mark the boundaries where periodicity in the $x$ direction is enforced. The green lines in figure 2 mark the starting point of the region where the nudging algorithm operates, with the left-hand side showing the horizontally homogeneous region used to nudge the downstream flow back to horizontally homogeneous flow that is unaware of the hill and the right-hand side showing the region that is nudged back to the upwind conditions. Periodic boundary conditions are imposed in the lateral ( $y$ ) direction, the upper boundary is a frictionless rigid lid, and the lower boundary beneath the trees uses a rough-wall neutrally stratified drag law with a surface roughness length $z_{\circ } = 1\times 10^{-3}$ m.

To minimize the computational expense, all the simulations are generated by first integrating a smaller $512\times 512\times 256$ grid point flat-domain simulation out in time using periodic horizontal boundary conditions until the initially laminar flow develops from divergence free random fluctuations into 3D turbulence that is in equilibrium with the imposed pressure gradient. Upon reaching equilibrium, a restart volume is saved. This volume is then mirrored one time in the lateral ( $y$ ) and four times in the downwind ( $x$ ) directions to create a fully turbulent initial condition for the full large-domain simulations. The code is then reconfigured to: (i) restart from this larger volume, and (ii) run using the precursor inflow boundary condition in the along-wind ( $x$ ) direction. Upon restart, a hill is gradually grown into the downwind portion of the domain over a period of 400 s. Averaging begins after integrating forward in this configuration for approximately one large-eddy turnover time to allow the turbulence to evolve into the new configuration. Running on 2048 CPUs on an HPE SGI ICE XA system (Computational and Information Systems Laboratory 2019), the (2D; 3D)-hill simulations required approximately (77; 366) wallclock hours, respectively.

As in the WT measurements (Harman & Finnigan Reference Harman and Finnigan2018), the flow is neutrally stratified (no buoyancy) and Coriolis forces are ignored. The hills are of cosine shape,

(3.2) \begin{align} \quad \quad \quad \quad h(x,y) &= H \, {\textrm{cos}}^2\left (\frac {\pi \; \widehat {x}}{4}\right ) &\text{when} \quad |\,\widehat {x}\,| \le 2, \quad \quad \quad \quad \end{align}

(3.3) \begin{align} \quad \quad \quad \quad h(x,y) &= 0 &\text{when} \quad |\,\widehat {x}\,| \gt 2, \quad \quad \quad \quad \end{align}

where, $H$ is the hill height. In the 2D-hill case,

(3.4) \begin{equation} \widehat {x} = \frac {x - x_{\circ }}{L_x} ,\end{equation}

and, in the 3D-hill case,

(3.5) \begin{equation} \widehat {x} = \left [ \left (\frac {x - x_{\circ }}{L_x}\right )^2 + \left (\frac {y - y_{\circ }}{L_y}\right )^2 \right ]^{\frac {1}{2}}\!, \end{equation}

where $L_x$ and $L_y$ are the hill lengths at the hill half-height in the $x$ and $y$ directions, respectively, and ( $x_{\circ }, y_{\circ }$ ) represent the physical location of the hill crest. In the axisymmetric 3D hill simulations, $L_x = L_y = L$ . Variations in hill steepness are generated by keeping $H$ fixed and varying $L$ . Scaling up the WT hills by a factor of 256, $H = 12.8$ m for all cases; see table 1 for the matching values of $L$ . Figure 3 shows examples of the surfaces investigated with the LES. The $x$ , $y$ grid lines follow this surface and algebraically relax back to horizontal grid lines parallel to the upwind flat surface at approximately the domain half-height (see (4) in Sullivan et al. (Reference Sullivan, McWilliams and Patton2014), where we use $\varpi = 3$ ).

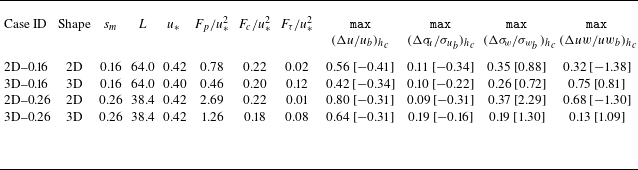
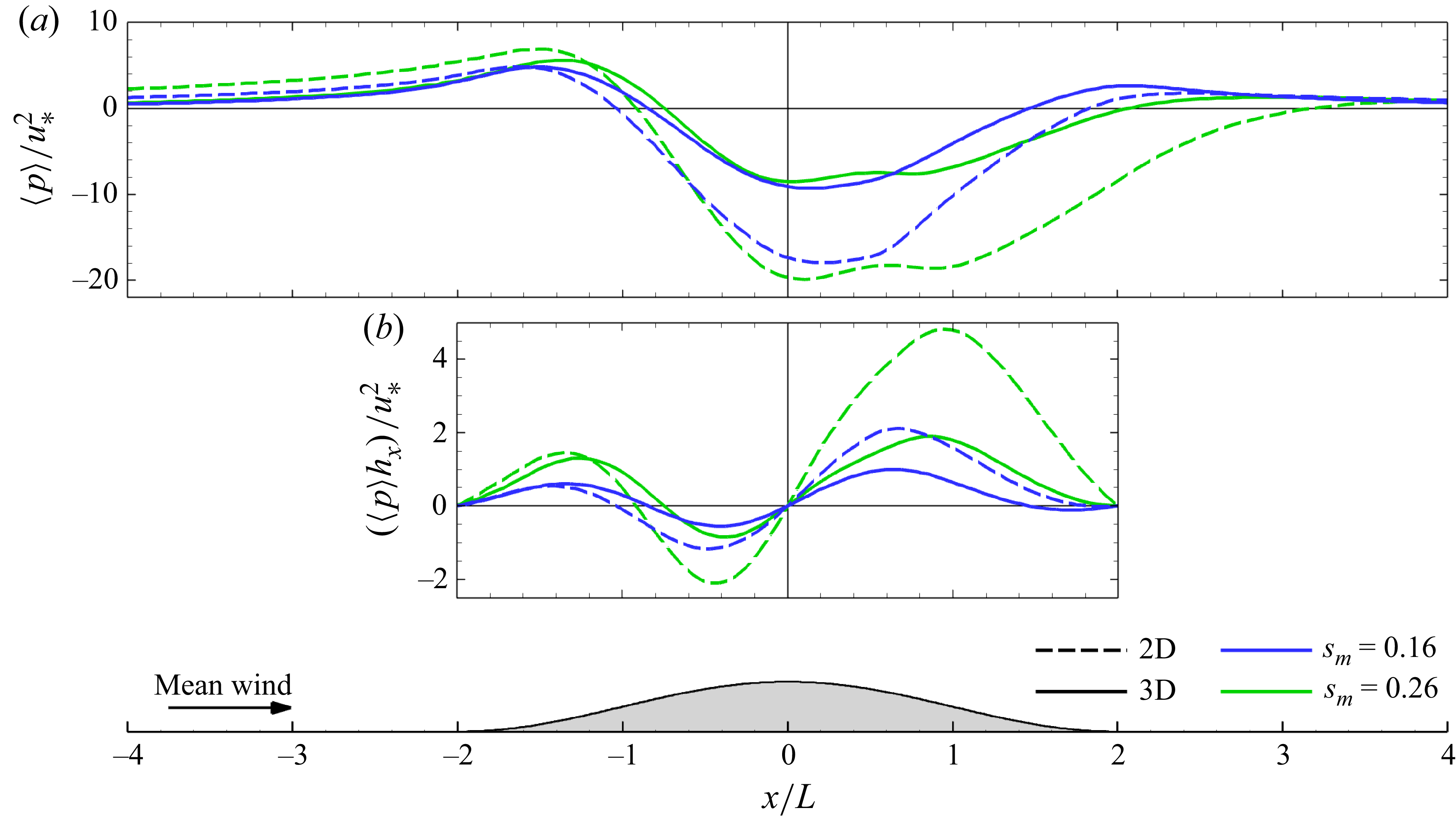
Table 1.

Bulk parameters from each of the four simulations. Here $s_m$ is the maximum hill slope ( $\text {max}( {\partial h}/{\partial x})$ ), $L$ is the length of the hill (m) in the streamwise direction $x$ at half the hill height (so the total hill length is 4L), $u_*$ is the friction velocity (m s $^{-1}$ ) evaluated at $x = -4L$ and $z = h_c$ (consistent with $u_*$ observed in the WT; when averaged over the entire upwind periodic domain, $u_* = 0.42$ m s $^{-1}$ for all cases). Here $F_p = - \int _{-2L}^{2L}\langle p \rangle h_x\,{\rm d}x$ is the streamwise surface pressure drag integrated over the hill (e.g. the hill-induced pressure force on the air) normalized by $u_*^2$ , where $h_x = {\partial h}/{\partial x}$ is the $x$ -varying hill slope), $F_c = - \,c_d\,a \int _{-2L}^{2L}\int _{0}^{h_c} \langle |u_i| u \rangle \,{\rm d}z\,{\rm d}x$ is the hill- and canopy-integrated drag induced by the canopy in the streamwise direction and $F_{\tau } = \int _{-2L}^{2L}\langle u'w' \rangle \,{\rm d}x$ is the hill-integrated streamwise surface stress; the total drag felt by the flow over the hill $F_T = F_p + F_c + F_{\tau }$ . Here max $(\Delta u/u_b)_{ h_c}$ , max $(\Delta \sigma _{\!u}/\sigma _{u_b})_{ h_c}$ , max $(\Delta \sigma _{\!w}/\sigma _{w_b})_{ h_c}$ and max $(\Delta uw/uw_b)_{ h_c}$ are the maximum hill- and canopy-induced speedup, standard deviation of streamwise and vertical velocity, and vertical flux of streamwise momentum increase at canopy top along hill centreline, respectively, where $\Delta u/u_b = [(\langle u \rangle - \langle u \rangle _{b}) / \langle u \rangle _{b}]$ , $\Delta \sigma _{u}/\sigma _{u_b} = [(\sigma _u - \sigma _{u_{b}}) / \sigma _{u_{b}}]$ , $\Delta \sigma _w/\sigma _{w_{b}} = [(\sigma _w - \sigma _{w_{b}}) / \sigma _{w_{b}}]$ and $\Delta uw/uw_b = [(\langle u'w' \rangle - \langle u'w' \rangle _{b}) / \langle u'w' \rangle _{b}]$ evaluated at a height of $h_c$ above the local surface $h$ , the notation $_{b}$ refers to a reference value upwind of the hill (Appendix A) and the adjacent values in square brackets reflects the $x/L$ location where the maximum canopy-top value is found.

The canopy parameters are derived directly from measurements of the rods used in the WT experiments (Harman & Finnigan Reference Harman and Finnigan2018). In the WT, the rods are 15 mm tall, 5 mm in diameter ( $d_r$ ), and are spaced at 12.5 mm intervals in the $x$ direction and 25 mm in the $y$ direction. Hence, the number of rods per unit area $n_r$ = 3200 m $^{-2}$ and the rods have a frontal area density $a = n_r \times r_d =$ 16 m $^2$ m $^{-3}$ that is constant with height. Fitting the WT observed profiles with the rods installed on flat terrain (Harman & Finnigan Reference Harman and Finnigan2018, figure 2 a) to the Harman & Finnigan (Reference Harman and Finnigan2007) roughness sublayer (RSL) theory reveals that the rods have an effective canopy length scale $L_c = (c_d\,a)^{-1}$ = 110 mm. Therefore, the drag coefficient $c_d$ of the rods is 0.57. In the numerical simulations, these rod parameters are applied to a canopy of height $h_c$ = 3.84 m resolved by nine grid points on the flat portion of the domain and by 10 grid points at the hill crest due to the terrain following coordinate system. To mimic the WT experiments, the canopy is prescribed to be horizontally homogeneous for all four simulations. Figure 1 shows an image of the WT configuration with the steep-sloped ( $s_m =$ 0.26) axisymmetric canopy-covered hill installed.

Figure 3.

A zoomed presentation of the 2D (a) and 3D-axisymmetric (b) cosine hills interrogated. In (a), $L = L_x$ and $L_y$ is not defined, and in (b) $L = L_x = L_y$ . $H$ is the hill height (3.2). The green surface depicts canopy top $h_c$ .

To classify the current simulations within the context of previous work, we first turn to the Hunt et al. (Reference Hunt, Leibovich and Richards1988) and Finnigan & Belcher (Reference Finnigan and Belcher2004) theories discussed in § 2. In both theories, the middle layer depth ( $h_m$ ) is defined as $h_m \sim L\,[\text{ln}(h_m / z_{\circ })]^{{1}/{2}}$ , and the inner layer depth ( $h_i$ ) is defined as $h_i \sim 2\,L\,\kappa ^2 / \text{ln}(h_i / z_{\circ })$ , where $\kappa$ is von Kármán’s constant. However, calculating $h_i$ and $h_m$ using these formulations can lead to physically implausible values over surfaces covered with tall roughness, i.e. $h_i$ can end up being found at heights within the canopy of roughness elements (Finnigan et al. Reference Finnigan, Raupach, Bradley and Aldis1990). Therefore, Appendix B derives new formulae for $h_i$ and $h_m$ incorporating changes to the logarithmic mean velocity profile and the accompanying flux-gradient relationship which occur over a tall plant canopy (Harman & Finnigan Reference Harman and Finnigan2007, Reference Harman and Finnigan2008); labelled $\widehat {h_m}$ and $\widehat {h_i}$ using similar notation to Harman & Finnigan (Reference Harman and Finnigan2007, Reference Harman and Finnigan2008). For the configurations discussed here, $\widehat {h_m}$ $\sim$ (32.8, 21.7) m and $\widehat {h_i}$ $\sim$ (11.8, 9.8) m for cases with $s_m =$ (0.16, 0.26), respectively, where these values represent their physical height above the origin of the above-canopy coordinates $z = d + z_{\circ }$ in the upwind flow (Appendix B). For reference, $h_i$ for the current configuration using this same reference height is $\sim$ (9.3, 7.2) m, respectively, and $h_m = \widehat {h_m}$ .

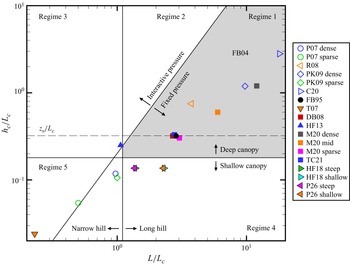
Figure 4.

Length scale regime diagram following Poggi et al. (Reference Poggi, Katul, Finnigan and Belcher2008) mapping the hill geometry and canopy morphology of the current numerical (labelled P26) and WT (Harman & Finnigan Reference Harman and Finnigan2018, HF18) simulations relative to previous research on turbulent flow over low forested hills. Here, low hills implies that $H/L \ll 1$ with $H$ the hill height, and $L$ the hill half-length at half the hill height. Here $h_c$ is the canopy height, and $L_c$ is the canopy adjustment length. Low hills with $L/L_c \lt 1.1$ are deemed `narrow’, and with $L/L_c \gt 1.1$ ‘long’. Canopies with $h_c/L_c \lt 0.18$ are deemed ‘shallow’, and $h_c/L_c \gt 0.18$ `deep’, where $0.18 = 2\beta ^2$ when $\beta = {u_*}/{u}|_{h_c} = 0.3$ . From Finnigan & Belcher (Reference Finnigan and Belcher2004, FB04), the envelope $h_c/L_c = 2(H/L)(L/L_c)^2$ delineates the regime in which the mean within-canopy vertical velocity is expected to be sufficiently large to affect the outer layer pressure. Previous research included Finnigan & Brunet (Reference Finnigan, Brunet, Coutts and Grace1995, FB95), Tamura et al. (Reference Tamura, Okuno and Sugio2007, T07, where $\beta = 0.3$ is assumed), Poggi et al. (Reference Poggi, Katul, Albertson and Ridolfi2007, P07), Dupont & Brunet (Reference Dupont and Brunet2008, DB08), Ross (Reference Ross2008, R08), Patton & Katul (Reference Patton and Katul2009, PK09), Harman & Finnigan (Reference Harman and Finnigan2013, HF13), Ma et al. (Reference Ma, Liu, Banerjee, Katul, Yi and Pardyjak2020, M20), Chen et al. (Reference Chen, Chamecki and Katul2020, C20) and Tolladay & Chemel (Reference Tolladay and Chemel2021, TC21). Open symbols reflect work on sinusoidally repeating low forested hills, and filled symbols reflect work on isolated forested hills. Symbols without a black outline study flow over low 2D forested hills (ridges), those with a black outline study flow over low 3D forested hills. The thin long-dash black line marks the canopy height at which one would expect separation $z_s$ for the current canopy configuration according to FB04.

Secondly, figure 4 presents a regime diagram following that proposed by Poggi et al. (Reference Poggi, Katul, Finnigan and Belcher2008) that characterizes the simulations based upon key length scales determining canopy influences on the flow. The length scales of importance are the canopy height $h_c$ , canopy adjustment length $L_c$ and the hill half-length at half the hill height $L$ . Regime 1 marks the region where the Finnigan & Belcher (Reference Finnigan and Belcher2004, FB04) theory is valid. In Regime 2, deviations from the FB04 theory can be attributed to within-canopy vertical velocities being of sufficient amplitude to alter the pressure in the inner layer above the canopy; i.e. when $L/L_c$ is large, the canopy flow adjusts to the pressure gradient more rapidly than the pressure gradient changes (Belcher, Harman & Finnigan Reference Belcher, Harman and Finnigan2011). In Regime 3, such deviations can be attributed to both pressure and advection. In Regime 4, the canopy is insufficiently deep or dense to absorb all the momentum and hence within-canopy turbulence is influenced by finite shear stress at the underlying surface. All of these processes are at play for flows in Regime 5. Figure 4 shows that the current simulations fall within Regime 4, a regime that falls outside the applicability of current theory (e.g. Finnigan & Belcher Reference Finnigan and Belcher2004; Harman & Finnigan Reference Harman and Finnigan2009, Reference Harman and Finnigan2013) and which has not received much attention in the literature.

The numerical and physical WT simulations differ in that a constant external pressure gradient ( $\varPi _x = 1.63\times 10^{-4}$ m s $^{-2}$ , selected to reproduce $u_*$ observed in the tunnel) drives the flow in the $x$ -direction in the LES, while the WT is a zero pressure-gradient tunnel. The flow sampled in the WT therefore represents an internal boundary layer driven by downward transport of momentum from the free stream airflow above, while the LES simulations represent a pressure-gradient driven fully developed boundary layer that is turbulent throughout the domain.

Another aspect of the numerical simulations that differs from the WT physical simulations is that the numerical simulations use periodic boundary conditions in the lateral direction, while the WT has viscous sidewall boundary layers. The horizontal dimensions of the numerical simulation domain are selected to ensure that the flow interacting with the 3D hills remains independent of the problem design. In the configuration with 3D hills (table 1), the hill only occupies a maximum of $\sim$ 3 % of the lateral domain that should ensure that any hill-induced flow perturbations are negligible at the lateral boundaries.

4. Analysis procedures

Analysis of the 2D- and 3D-hill simulations differ because the 2D simulations contain an homogeneous horizontal direction, i.e. the lateral ( $y$ ) direction, while the 3D simulations do not. In the 2D-hill case, mean flow fields and higher moments are laterally averaged and time-averaged during the simulation and statistics are calculated during postprocessing. Analysis of the 3D simulations relies solely upon time averages (analogous to single-point WT measurements) based upon first-, second- and third-order moments calculated at every time step during the simulation. For the 2D-hill cases, a turbulent fluctuation is defined as a deviation from an instantaneous lateral average and higher moments are calculated as laterally averaged products which are then time-averaged over the duration of the simulation. For the 3D-hill cases, a turbulent fluctuation is defined as a deviation from a time-average at a single point and higher moments are calculated as time-averaged products of those fluctuations. The notation $\langle \phantom {\,}\rangle$ is used to denote a mean and a $'$ for a fluctuation from that mean.

To compare the numerical and WT simulations, all flow variables are normalized by time-averaged friction velocity $u_*$ evaluated at canopy top ( $z/h_c = 1$ ) and at $x/L = -4$ , which is characteristic of the undisturbed flow approaching the hill. The actual $u_*$ values derived from the simulations can be found in table 1, note that the small $u_*$ variations shown in table 1 reflect a slight need for additional averaging. The simulations are currently averaged over 150 000 time steps (or, if we define a large-eddy turnover time $\tau _{\ell }$ as the height of the domain (512 m) divided by the friction velocity $u_*$ , 150 000 time steps is $\sim$ 8 $\tau _{\ell }$ ). Two characteristic length scales are used: (i) the length of the hill at half its height in the along-wind direction $L$ , and (ii) the canopy height $h_c$ .

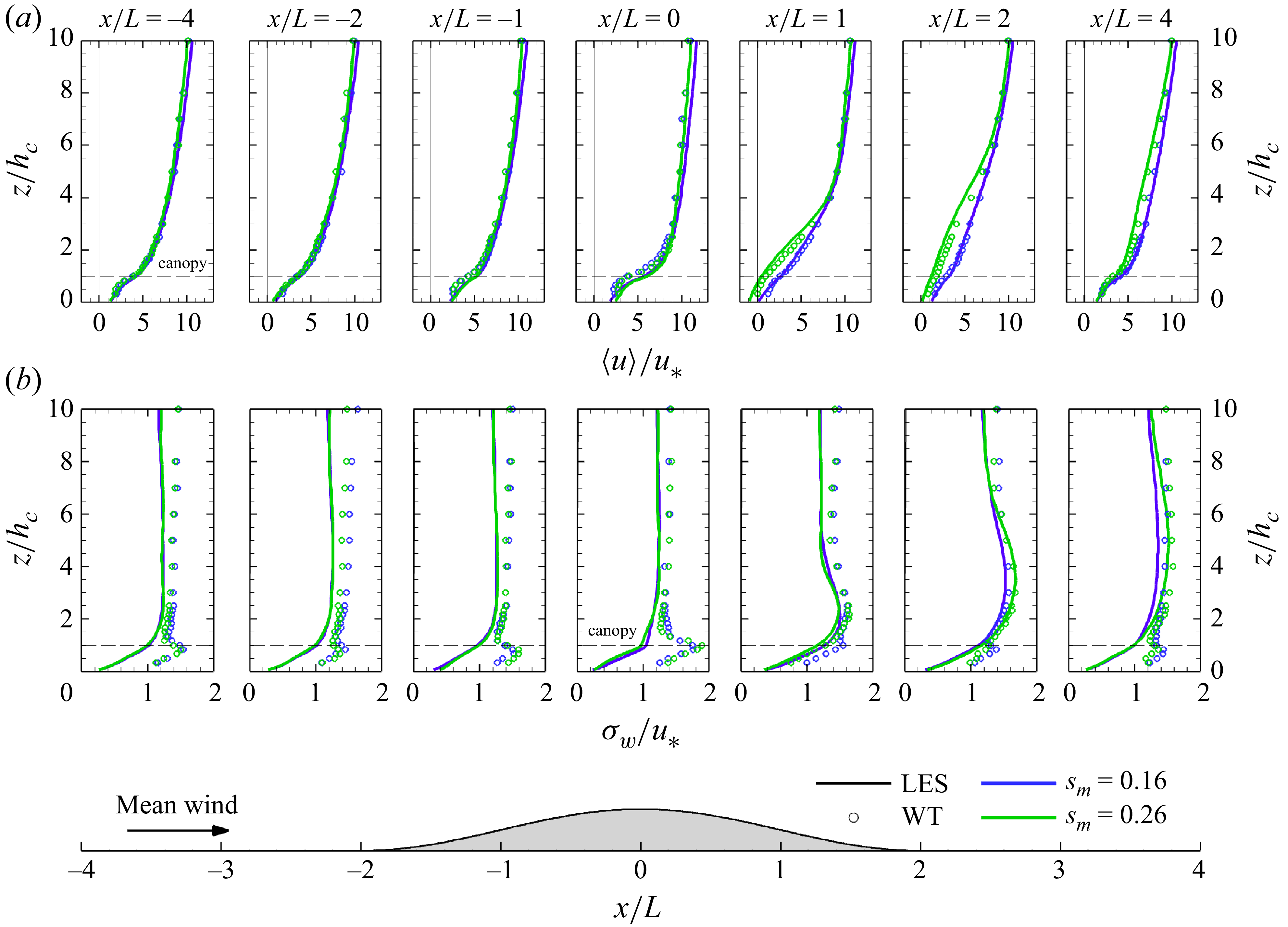
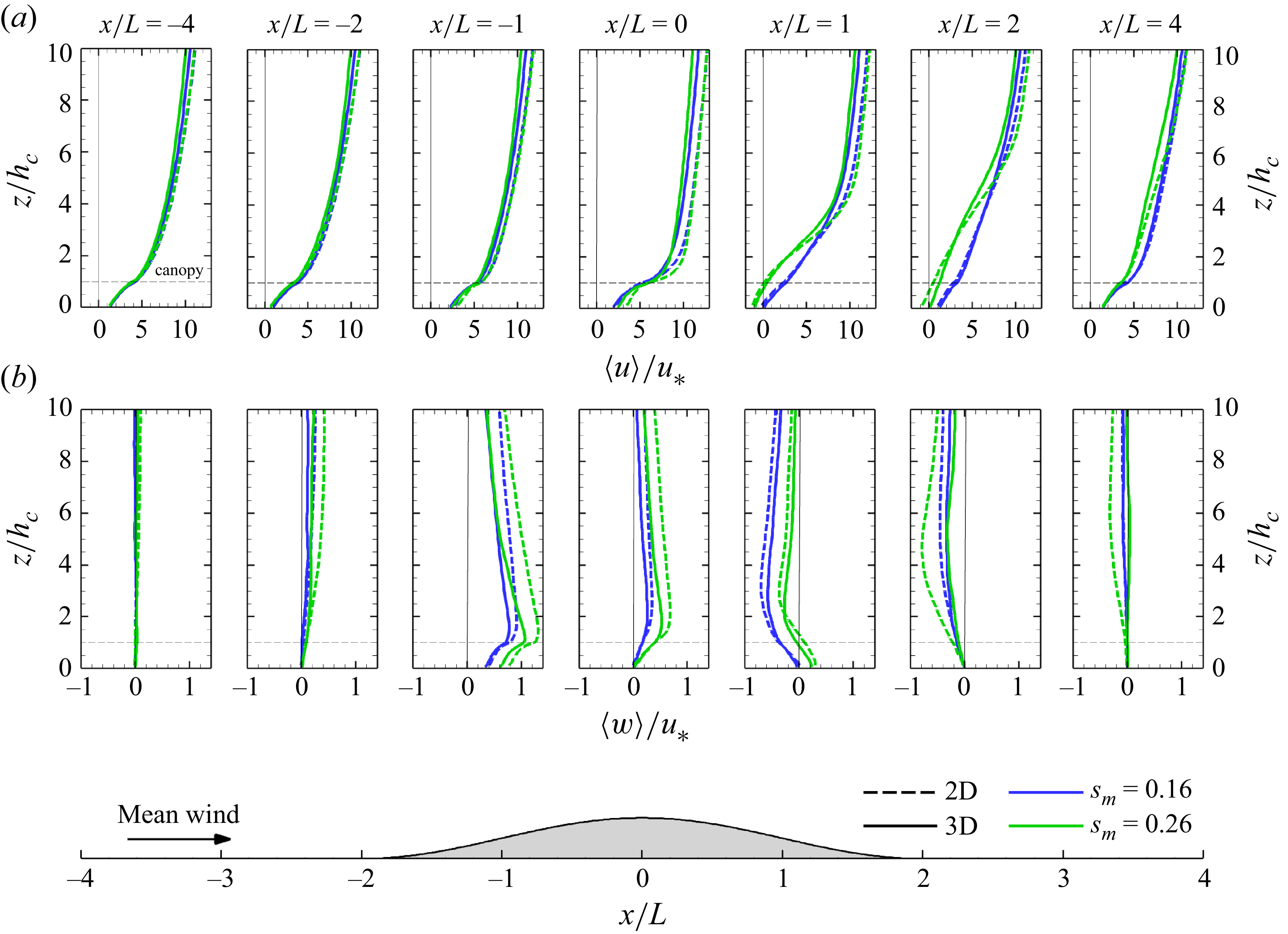
Figure 5.

A comparison of WT observed (symbols) and numerically simulated (lines) vertical profiles of average streamwise velocity, $u$ (a), and vertical velocity standard deviation, $\sigma _w$ (b), at hill centreline over axisymmetric hills normalized by the friction velocity $u_*$ . Blue colours reflect results for the case with $s_m =$ 0.16, and green colours reflect results for the case with a slope $s_m =$ 0.26; for the LES the data are from 3D–0.16 and 3D–0.26, respectively. The mean flow direction in these figures is from left to right (in the $+x$ direction). In these figures, we are using a coordinate system that is aligned with (and perpendicular to) the flat terrain surrounding the hill, so positive $u$ is in the $+x$ direction, and positive $w$ is upward.

5. Comparison with WT measurements

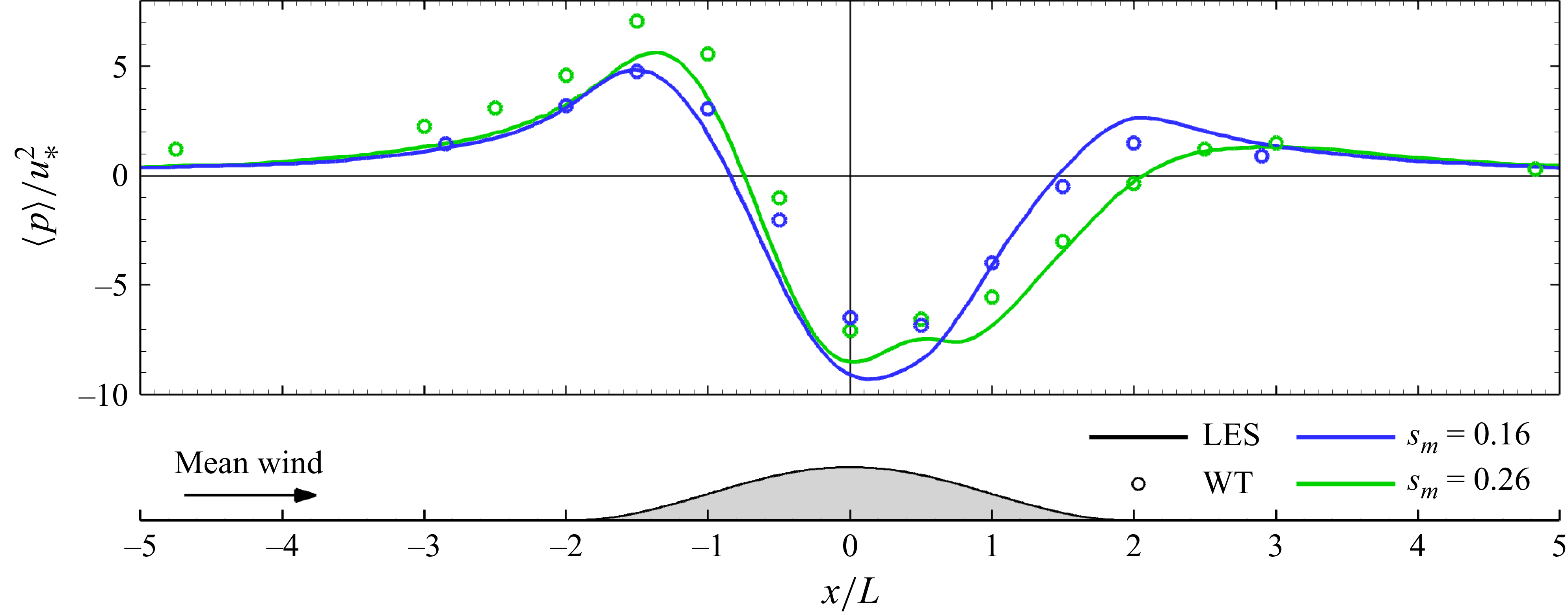
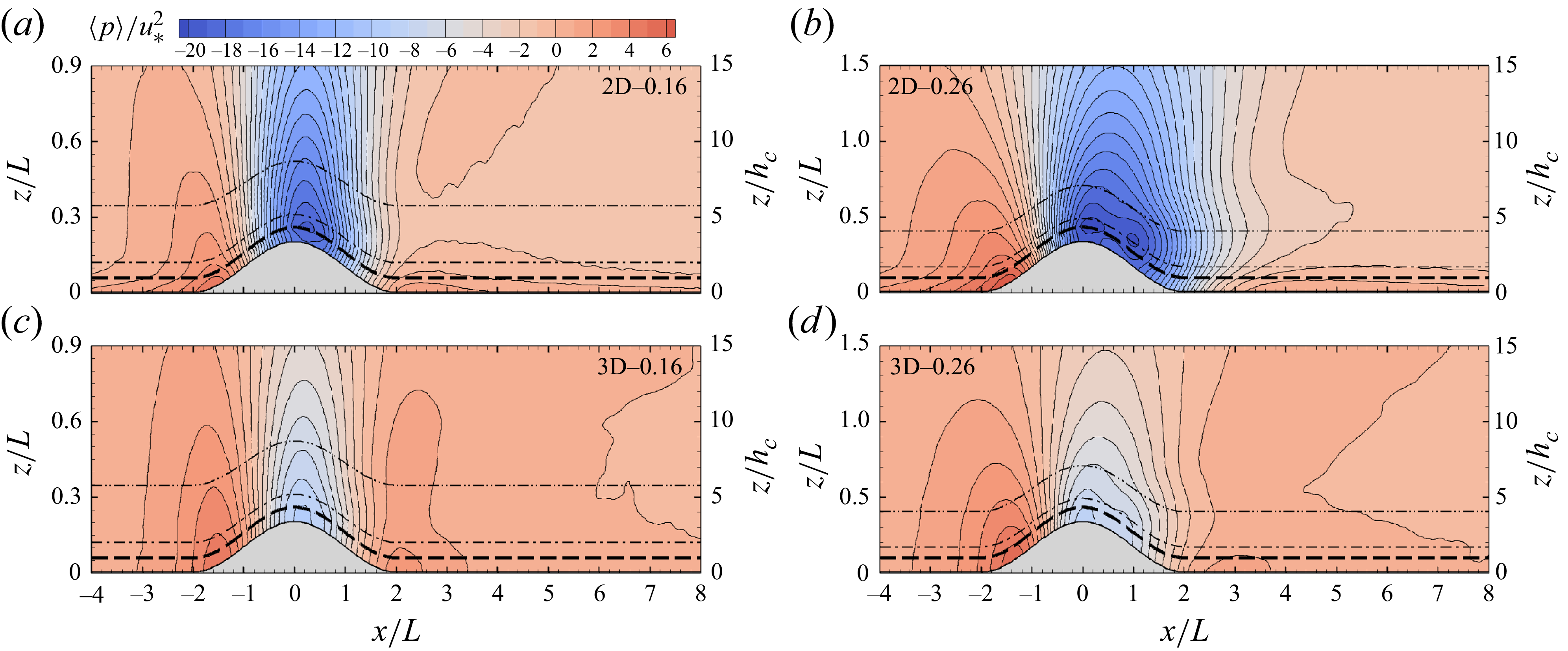
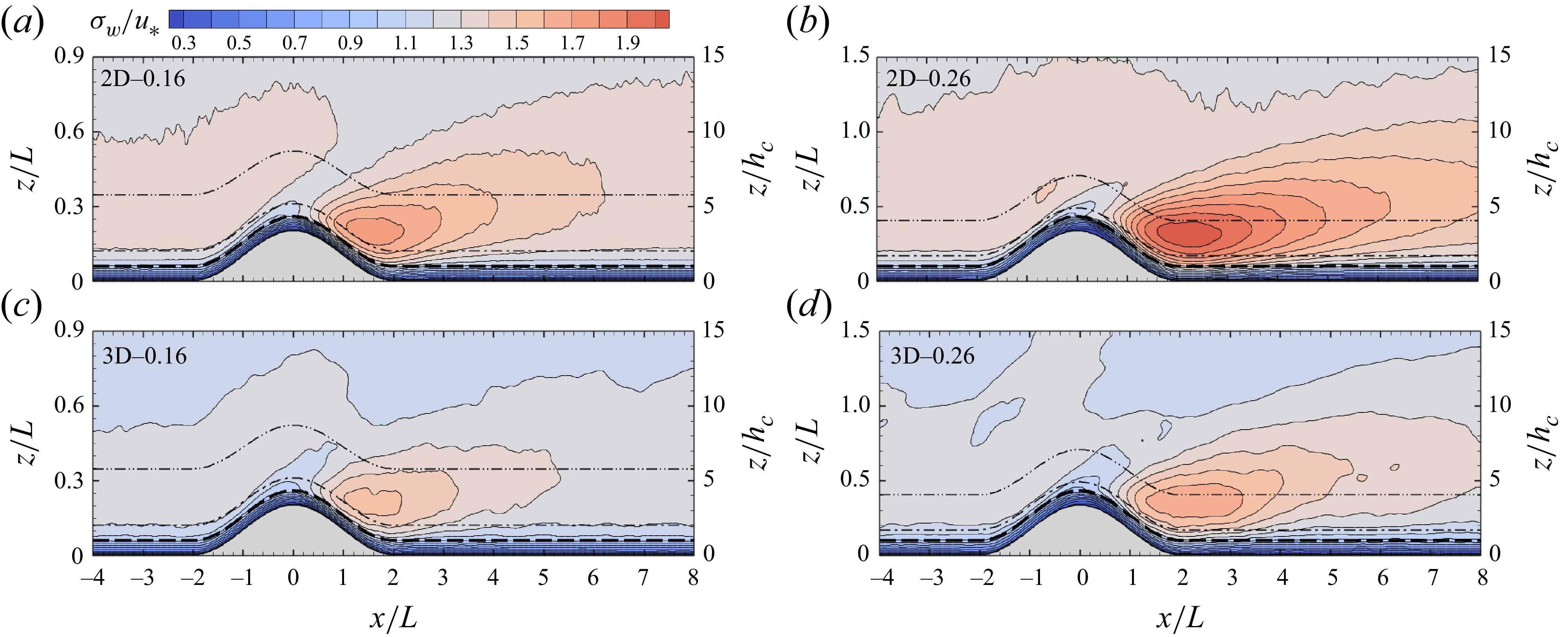
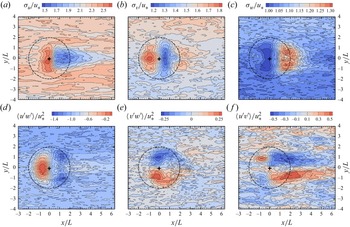
5.2. Pressure

In the absence of a canopy, the surface pressure perturbation induced by neutral flow encountering an isolated obstruction exhibits an initial peak associated with flow stagnation on the upwind side of the obstruction, a pressure minimum at the hill crest resulting from the flow acceleration over the hill, followed by a second pressure peak on the hill’s leeward side as the flow moving over the hill encounters the flat surface again and then recovers downwind of the hill to its undisturbed upwind state (e.g. Jackson & Hunt Reference Jackson and Hunt1975; Hunt et al. Reference Hunt, Leibovich and Richards1988). Theory suggests that because canopies interact with the flow through pressure, that the presence of vegetation on hills can shift the pressure distribution sufficiently to make forested hills appear steeper than one would anticipate (e.g. Finnigan & Belcher Reference Finnigan and Belcher2004). Asymmetries in and phase shifts of the surface pressure perturbations relative to the hill define the orographic surface drag felt by the flow and dictate whether flow separation will occur on leeward slopes (e.g. Belcher et al. Reference Belcher, Harman and Finnigan2011). Therefore, the surface pressure distribution reflects the overall hill- and canopy-induced influence on the flow and represents a key metric whose accuracy needs to be demonstrated.

Figure 6.

A comparison streamwise transects of normalized surface pressure variations at hill centreline normalized by $u_*^2$ for 3D forested hills of two slopes ( $s_m =$ 0.16 (blue colours) and 0.26 (green colours)); for the LES, these results are from cases 3D–0.16 and 3D–0.26, respectively. Solid lines represent LES results, and symbols reflect the WT measurements.

During the WT experiments, a manifold system sampled the surface pressure via tubes inserted into holes drilled into the hill surface (Harman & Finnigan Reference Harman and Finnigan2018). Comparing observed and simulated along-wind surface pressure variations normalized by $u_*^2$ at hill centreline (figure 6) reveals broad overall agreement between the WT and the LES of the location and phasing of the pressure maxima and minima for both hill slopes. On the windward side of the hill, the pressure peak in the steep hill case is of slightly higher magnitude in the WT than in the LES, while the pressure minima near hill-centre or just downwind of the crest is of higher magnitude in the LES than the WT; which, in combination implies a slightly larger surface pressure gradient driving the flow in the LES producing the slightly higher in-canopy wind speeds shown in figure 5. These features likely result from our decision for the LES simulations to target outdoor situations and the associated taller LES domain compared with the depth of the boundary layer in the WT, but do not negatively influence confidence in the LES solutions.

The results presented in figures 5 and 6 provide evidence that the LES and its configuration accurately simulates turbulent flows over isolated 3D hills. Therefore, the LES results can now offer insight into aspects of flow over 2D or 3D forested hills that are difficult to observe.

6. Flow over 2D versus 3D forested hills

Flow over isolated hills differs from flow over repeating 2D cosine hills, because in the latter the flow approaching any single hill feels the influence of the hill just upstream and all previous hill adjustments (e.g. Belcher et al. Reference Belcher, Newley and Hunt1993). Turbulent flow over isolated 2D and 3D hills differ substantially due to the ability for the flow to leak around the sides of 3D hills (e.g. Mason & King Reference Mason and King1985). We now interrogate mean variations in the flow fields resulting from interactions with isolated 2D and 3D forested hills.

Figure 7.

Vertical slices of average streamwise velocity $\langle u \rangle$ normalized by the friction velocity $u_*$ . Panels (a) and (c) present results from the shallow-sloped hills ( $s_m =$ 0.16), and panels (b) and (d) from the steeper hills ( $s_m =$ 0.26). Panels (a) and (b) present time-averaged and laterally averaged 2D-hill results, panels (c) and (d) present time-averaged 3D-hill results. In all figures, the dashed black line depicts canopy top. All four figures use the same vertical axis relative to the canopy height ( $h_c$ ), which means that they’re presented up to different heights relative to the hill half-length ( $L$ ). The mean wind flow is from left to right (in the $+x$ direction). The white contour line marks zero streamwise velocity. The dash–dot line is $\zeta _i / h_c$ , and the dash–dot–dot line is $\zeta _m / h_c$ ; see § 7 for definition of $\zeta _i$ and $\zeta _m$ .

6.1. Mean wind

Figure 7 shows the influence of hill-shape and hill-slope on the vertical variation of mean streamwise velocity. It is important to recall that figure 7(a,b) present $y$ - and time-averaged 2D $x$ – $z$ slices, while figure 7(c,d) show time averages at hill centreline ( $y/L = 0$ ). It is also important to recall that flow variables ( $u$ , $v$ , $w$ ) represent flow in the ( $x$ , $y$ , $z$ ) directions.

Figure 8.

Vertical profiles of average streamwise (a) and vertical (b) velocity normalized by the friction velocity $u_*$ comparing the four cases. Dashed lines depict results for flow over the 2D hills, and solid lines depict results over 3D hills at hill centreline ( $y/L = 0$ ). Flow over the shallow-sloped hills ( $s_m =$ 0.16) are in blue, and flow over the steeper hills ( $s_m =$ 0.26) are in green. The mean wind flow is from left to right (in the $+x$ direction).

For the steeper hills ( $s_m = 0.26$ ), a separation bubble forms on the hill’s leeward side within the canopy for both hill-shapes (figure 7), where reverse flow spans the region between $0.67 \lt x/L \lt 2.29$ ( $0.67 \lt x/L \lt 1.93$ ) and extends vertically through the entire (most of the) canopy depth in the 2D (and 3D) cases, respectively. Flow separation also occurs intermittently over the shallower-sloped hills ( $s_m = 0.16$ ), but mean separation is only found in 2D–0.16 confined to regions very close to the surface and to $0.56 \lt x/L \lt 1.25$ . All cases reveal a within-canopy speed-up on the windward side of the hill occurring between approximately $-1.5 \le x/L \le -0.5$ . At a fixed height above the trees (e.g. $z/h_c = 10$ ), cases with shallower-sloped hills ( $s_m = 0.16$ , figure 7 a,c) result in higher average streamwise wind speeds for the same imposed pressure gradient compared with those with steeper hills (figure 7 b,d). A direct comparison of the 2D versus 3D flow fields at specified locations (figure 8) emphasizes these findings quantitatively. Overall, 2D-hills induce larger amplitude streamwise $\langle u \rangle$ and vertical velocity $\langle w \rangle$ than do 3D hills, especially above the canopy; this result should be expected due to the ability for the flow impinging on the hill to leak around the sides of the 3D hills. At the foot of the windward side of the hill ( $x/L = -2$ ), all cases display non-zero $\langle w \rangle$ suggesting that the flow already feels the hill-induced pressure forces. At $x/L = -1$ , $\langle w \rangle$ at canopy top increases by nearly 11 % for 2D compared with 3D hills for cases with $s_m =$ 0.16, compared with a 19 % increase for cases with $s_m =$ 0.26. At hill-crest, $\langle w \rangle$ remains upward above and within the upper canopy. Canopy-top wind speeds are highest in the region between $x/L = -1$ and 0, but the largest vertical gradient in streamwise velocity is found near $x/L = 0$ . Reverse flow within the canopy is clearly apparent at $x/L = 1$ for the cases with $s_m = 0.26$ , i.e. negative streamwise velocity and positive vertical velocity within the canopy with both changing sign at canopy top. The 2D hill case with $s_m = 0.26$ clearly requires a longer distance downwind for $\langle w \rangle / u_*$ to relax back to conditions upwind wind of the hill, which has not occurred by $x/L = 4$ . In combination, the profiles in figure 8 demonstrate the increased role of mean vertical advection of streamwise momentum with increasing hill slope whose sign varies with position on the hill, and emphasize that care should be taken when comparing the current simulation results (where flow variables are presented in a coordinate system aligned with the upstream flat surface) and outdoor field measurements that rotate variables into a flow-dependent coordinate system forcing local $\langle w \rangle$ to zero (e.g. Wilczak, Oncley & Stage Reference Wilczak, Oncley and Stage2001; Finnigan et al. Reference Finnigan, Clement, Malhi, Leuning and Cleugh2003; Finnigan Reference Finnigan2004).

Figure 9.

Horizontal terrain-following (at constant $\zeta$ ) slices of time-averaged streamwise velocity, $\langle u \rangle$ (a,d), and spanwise velocity, $\langle v \rangle$ (b,e), and vertical velocity, $\langle w \rangle$ (c, f), at canopy top ( $\zeta /h_c\,\sim 1$ ) normalized by $u_*$ from the two 3D-hill simulations: (a–c) 3D–0.16; (d–f) 3D–0.26. The dashed black line depicts the location of the hill base at $\zeta /L = 0$ , and the black cross marks the hill-crest. The mean wind flow is from left to right (in the $+x$ direction).

Figure 9 shows terrain-following horizontal surfaces of $\langle u \rangle$ , spanwise $\langle v \rangle$ and vertical $\langle w \rangle$ velocity normalized by $u_*$ at canopy-top ( $z/h_c \sim$ 1) for the two 3D-hill cases and demonstrates the horizontal variability of mean wind fields induced by variations in hill-slope. Figure 9(a,d) show that increased hill slope dramatically increases the speed-up on the windward side and a slow-down on the leeward side. Maximum wind speeds at canopy-top occur on the windward side of the hill at approximately $x/L = -0.3$ (see $\texttt {max}(\Delta u/u_b)_{h_c}$ , table 1), and extend laterally to approximately $y/L = 1$ , while the peak wind-speed reduction at canopy-top on the leeward side occurs at approximately $x/L = 1.5$ and only extends laterally to approximately $y/L = 1$ . Note that these results differ from those in turbulent flow over unforested hills where the maximum speedup occurs at the hill-crest (e.g. Jackson & Hunt Reference Jackson and Hunt1975; Ayotte & Hughes Reference Ayotte and Hughes2004); Finnigan & Belcher (Reference Finnigan and Belcher2004) present an explanation describing the canopy-imposed mechanisms controlling this shift for flow over 2D-hills. With increasing hill steepness, maximum speedup at canopy top and at hill centreline increases and shifts up slightly downwind ( $\texttt {max}(\Delta u/u_b)_{h_c}$ , table 1).

Figure 9(b,e) demonstrate the horizontal distribution of the mean lateral velocity $v$ at canopy top induced by the 3D hills. Increased hill-slope also increases the magnitude of the hill-induced lateral velocity, with lateral velocities on the windward side of the hill ( $x/L \lt 0$ ) generally of lower magnitude than those on the leeward side ( $x/L \gt 0$ ). For both hill slopes, the lateral velocities are induced out to lateral regions approximately $y/L = \pm 3$ (as defined by $\langle v \rangle /u_* \gt \pm 0.2$ ). In the case with $s_m =$ 0.16, lateral velocities largely disappear by $x/L = 2$ , while the flow encountering the steeper hill ( $s_m =$ 0.26), lateral velocities at canopy top persist downwind of the hill to at least $x/L = 4$ . At the canopy top, the peak hill-induced upward $\langle w \rangle /u_*$ is found along the windward hill centreline at $x/L \simeq -0.75$ for both 3D-hill cases (figure 9 c,f), with the steeper hill ( $s_m =$ 0.26) generating a $\sim$ 40 % larger upward vertical velocity. Peak downward $\langle w \rangle /u_*$ at canopy top is found on the leeward side of the hills, with a single peak in the unseparated 3D–0.16 case along hill centreline at $x/L \simeq 1$ , and a $\sim$ 23 % lower amplitude double peak in the separated 3D–0.26 case located at $x/L \simeq 1.5$ and $y/L \simeq \pm -1$ .

Figure 10.

Spanwise vertical slices ( $y$ – $z$ ) of time-averaged spanwise velocity $v$ normalized by $u_*$ at three along-wind locations: (a) $x/L = -1$ ; (b) $x/L = 0$ ; (c) $x/L = 1$ ) from 3D–0.26. Positive $v$ is in the $+y$ direction. The dashed black line depicts canopy top ( $z/h_c = 1$ ). The mean streamwise wind flow is out of the page (in the $+x$ direction). Note that contour ranges and intervals differ between panels.

In the 3D hill cases, the canopy’s presence produces interesting lateral flow within the canopy (figure 10, showing spanwise vertical slices of $v$ at three different $x/L$ locations for the case with $s_m = 0.26$ ). On the upwind side of the hill (figure 10 a), the hill induced stagnation pressure (to be further discussed in § 6.2) produces diverging lateral flow out to approximately $y/L = \pm 3$ and vertically throughout the canopy and up to heights of approximately $z/L = 1$ ( $z/h_c = 10$ ). At hill centreline ( $x/L = 0$ , figure 10 b), the above canopy flow continues its divergent path around the hill. However, canopy drag sufficiently reduces the streamwise velocities within the canopy that the hill-induced lateral pressure gradients produces within-canopy uphill flow on either side of the 3D hill. This convergent within-canopy flow starts at lateral distances of at least $y/L = \pm 3$ . At $x/L = 1$ (figure 10 c), the lateral flow converges in the hill’s lee but over a shallower depth than is the divergent flow on the hill’s windward side. Similar lateral flow features are also found in the WT (Harman & Finnigan Reference Harman and Finnigan2018). This hill-induced within-canopy lateral flow likely has significant impact on the transport of surface- and canopy-emitted scalars and hence the interpretation of single-point scalar flux measurements in forested hilly terrain.

Figure 11.

Vertical slices of average pressure normalized by the friction velocity $u_*^{2}$ . Panels (a) and (c) present results from cases with shallow-sloped hills ( $s_m =$ 0.16), and panels (b) and (d) from cases with steeper hills ( $s_m =$ 0.26). Panels (a) and (b) present time-averaged and laterally averaged 2D-hill results, panels (c) and (d) present time-averaged 3D-hill results at hill-centreline. In all panels, the heavy dashed black line depicts canopy top, the dash–dot line $\zeta _i / h_c$ , and the dash–dot–dot line $\zeta _m / h_c$ (see § 7). All four panels use a consistent vertical axis relative to canopy height ( $h_c$ ), which means that they are presented up to different heights relative to the hill half-length ( $L$ ). The mean wind flow is from left to right (in the $+x$ direction).

Figure 12.

Horizontal terrain-following surfaces of time-averaged surface pressure, $\langle p \rangle$ (a,d), streamwise pressure gradient, ( $\partial \langle p \rangle / \partial x$ ) at $\zeta / h_c \sim 0.6$ (b,e) and spanwise pressure gradient ( $\partial \langle p \rangle / \partial y$ ) at $\zeta / h_c \sim 0.6$ (c, f) from the two 3D-hill simulations, normalized by appropriate combinations of $u_*^2$ and $h_c$ . Panels (a–c) depict results from 3D–0.16, and (d–f) from 3D–0.26. The dashed black line depicts the location of the hill base at $\zeta /L = 0$ , and the black cross marks the hill-crest. The mean wind flow is from left to right (in the $+x$ direction).

6.2. Pressure

Axisymmetric 3D hills produce slightly higher stagnation pressure peaks on the windward side of the hill, and notably reduced negative pressure near the hill crest compared with 2D hills (figure 11 and figure 12 a,d). This feature results from the impinging flow leaking around the lateral sides of the 3D hill compared with the 2D hill which produces more blockage as the flow is forced to go over the hill, hence 2D hills produce higher magnitude canopy-top wind speeds overall ( $\texttt {max}(\Delta u/u_b)_{h_c}$ , table 1). For both hill shapes, steeper hills ( $s_m =$ 0.26) shift the pressure minima more towards the hill crest compared with the shallower sloped hills ( $s_m =$ 0.16), but also broaden the along-wind region containing the minimum such that the lowest pressures span a region from approximately $-0.5 \le x/L \le 1.5$ (compared with $-0.2 \le x/L \le 0.9$ in the cases with shallower-sloped hills). Of note, however, is the secondary pressure minima in the hill lee in both the 2D–0.26 and the 3D–0.26 simulations (perhaps best seen in figure 13), a feature which has not been mentioned in previous studies of turbulent flow over forested hills and which therefore likely arises from the shallow canopy (Regime 4, figure 4) and its influence on flow separation.

Figure 12(b,e) and 12(c, f) present horizontal surfaces (constant $\zeta$ ) of the streamwise and spanwise pressure gradient induced by the 3D hills; these four panels show results at midcanopy height ( $\zeta / h_c \sim 0.6$ ) rather than at the surface like that in figure12(a,d). Clearly, the induced streamwise pressure gradient achieves larger amplitudes in the streamwise direction than in the spanwise direction. Compare $\texttt{max}$ $ (({\partial \langle p \rangle }/{\partial x})\,( {h_c}/{u_*^2}) )\sim (0.77, 1.56)$ and $\texttt{min}$ $ (( {\partial \langle p \rangle }/{\partial x})\,( {h_c}/{u_*^2} ))\sim (-0.64, -0.86)$ , respectively, for $s_m = (0.16, 0.26)$ , and for the spanwise direction for which the maxima/minima are symmetric, with $\texttt{max}/\texttt{min}$ $ (( {\partial \langle p \rangle }/{\partial y})\,( {h_c}/{u_*^2} ))\sim \pm(0.36, 0.59)$ for $s_m = (0.16, 0.26)$ , respectively. Although the spanwise pressure gradients are of lower magnitude from that in the streamwise direction, the lateral uphill in-canopy flows seen in figure 10 in the case with $s_m = 0.26$ at $x/L = 0$ suggest that the hill-induced spanwise pressure gradient is of sufficient magnitude to dominate downward transport of momentum down into the canopy along the sides of the 3D hills. Compared with the case with $s_m = 0.16$ , the case with $s_m = 0.26$ also shows strong lateral pressure gradients downwind of hill crest, but concentrated primarily in regions out towards hill-base.

Figure 13.

(a) A comparison of surface pressure ( $\langle p \rangle$ ) over 2D (dashed lines) and 3D (solid lines) hills. Hills with $s_m =$ 0.16, blue lines; and with $s_m =$ 0.26, green lines. Note that the solid lines in this panel are the same as those in figure 6. (b) A comparison of the negative correlation between the pressure distributions shown in (a) and the local hill slope ( $h_x = \partial h / \partial x$ ) at hill centreline normalized by $u_*^2$ for all simulations; i.e. the longitudinal variation of the hill- and canopy-induced pressure drag, where positive (negative) values represent a force acting to decelerate (accelerate) the flow, respectively. Results in both panels are laterally averaged for cases with 2D hills, and time-averaged along hill-centreline for cases with 3D hills.

Figure 13(a) shows a comparison of the horizontal variation of normalized surface pressure along the hill-centreline for the four cases. Figure 13(b) shows the correlation between the mean hill-induced surface pressure perturbations $\langle p \rangle$ and the local hill slope $h_x$ , where the integral under these curves represent the pressure drag in the $x$ direction at hill centreline (see $F_p$ in table 1). In all cases as the flow approaches the hill (from left to right in the figure), it first feels a pressure force retarding the flow (e.g. stagnation, positive $\langle p \rangle \,h_x$ ); an increase of 10 % in hill slope increases the pressure force in this region by approximately a factor of four. The amplitude and streamwise horizontal region over which this force acts also evolves with variations in hill-shape; where for 2D hills this retarding force acts over a smaller horizontal extent than it does for 3D hills, and the horizontal extent over which this retarding force acts increases with increasing hill-steepness. At a location somewhere between $-1.1 \le x/L \le -0.7$ , pressure drag changes sign to become an accelerating force (e.g. a thrust, negative $\langle p \rangle \,h_x$ ). Again, the spatial region over which this thrust acts on the flow increases with increasing hill steepness, however, the horizontal extent over which it acts decreases as the hills change from a 2D ridge to an axisymmetric 3D hill. Pressure drag acts to retard the flow (positive $\langle p \rangle \,h_x$ ) across nearly the entire leeward side of the hill for all cases, with the exception of a small region of acceleration (thrust) that develops in the cases with shallower slopes (i.e. between $1.5 \lesssim x/L \le 2$ ). The region of maximum pressure drag on the leeward side shifts downstream with increasing hill steepness.

Consistent with Ross & Vosper (Reference Ross and Vosper2005) and Poggi & Katul (Reference Poggi and Katul2007a ,Reference Poggi and Katul b ), peak minimum pressure is generally found at or just downstream of hill crest ( $0 \lesssim x/L \lesssim 0.5$ ), however, both of the $s_m = 0.26$ cases interestingly show a surface pressure increase at $0.5 \lesssim x/L \lesssim 0.6$ not present in either of the $s_m = 0.16$ cases (figure 13 a). 2D–0.16 in figure 11 shows a similar pressure increase in the midcanopy and above, suggesting that this pressure increase might result from an interaction of canopy processes and the hill-induced large scale pressure field. Figure 8 also shows that the mean flow reverses in the lower-canopy to midcanopy in the region $1 \lesssim x/L \lesssim 2$ . Therefore, this secondary pressure peak might result from the stagnation associated with the positive within-canopy streamwise velocity $\langle u \rangle /u_*$ at $x/L = 0$ and the reversed streamwise flow at $x/L = 1$ . This secondary pressure increase in the lee of steeper $s_m = 0.26$ hills for flows in Regime 4 contradicts Poggi & Katul’s (Reference Poggi and Katul2007a ) suggestion to estimate hill-induced pressure perturbations based upon the effective (or apparent) surface determined by the windward terrain surface and the leeward separation bubble.

6.3. Turbulence

Figure 14.

Vertical slices of the average standard deviation of vertical velocity $\sigma _w$ normalized by $u_*$ from all four simulations. Same layout as for figure 7. The mean wind flow is from left to right (in the $+x$ direction).

All cases generate an increase in the normalized standard deviation of vertical velocity $\sigma _w / u_*$ on the leeward side of the hill (figure 14) resulting from the hill-induced elevated shear layer in the hill’s lee. Generally, this leeward increase of $\sigma _w / u_*$ is of larger magnitude in the 2D hill cases (figure 14 a,b) than in the 3D hill cases (figure 14 c,d) with peak values of approximately 1.6 in the lower sloped case ( $s_m =$ 0.16) over the region between $1 \lt x/L \lt 2$ for both the 2D and 3D hills, while for the steeper hills ( $s_m =$ 0.26) $\sigma _w / u_*$ peaks at approximately 1.9 over the region spanning approximately $1 \lt x/L \lt 3$ ; accentuated vertical velocity fluctuation amplitudes persist downwind to well beyond $x/L = 8$ (or $x/h_c = 80$ ) and extend vertically up to heights above $z/L = 1.2$ (or $z/h_c = 12$ ) with the maximum change in $\sigma _w$ at canopy top $\Delta \sigma _{w_{{h_c}}}$ occurring at $x/L \sim 0.8$ for flow over the hills with $s_m =$ 0.16 and at $x/L \sim (2.3, 1.3)$ for the (2D, 3D) hills with $s_m =$ 0.26 (table 1).

Figure 15.

Vertical profiles of the standard deviation of streamwise velocity (a) and vertical velocity (b) normalized by the friction velocity $u_*$ comparing the four cases at $x/L = (-4, -2, -1, 0, 1, 2, 4)$ . Panel (c) presents vertical profiles of the vertical flux of streamwise momentum $\langle u'w' \rangle$ normalized by $u_*^2$ at the same $x/L$ locations. Dashed lines depict results for flow over the 2D hills, and solid lines depict results over 3D hills at hill centreline ( $y/L = 0$ ). Flow over the shallow-sloped hills ( $s_m =$ 0.16) are in blue, and flow over the steeper hills ( $s_m =$ 0.26) are in green. The mean wind flow is from left to right (in the $+x$ direction).

The streamwise variation of vertical profiles of turbulent flow statistics along hill centreline help quantify the influence of hill shape and steepness (figure 15). Upwind of the hill ( $x/L \sim -4$ ), ( $\sigma _u$ , $\sigma _w$ ) $/u_*$ above canopy-top match their theoretically expected (e.g. Lumley & Panofsky Reference Lumley and Panofsky1964) values $\sim$ (2.3, 1.3), respectively, and $\langle u'w' \rangle /u_*^2$ is nearly constant with height at a value of $-1$ . Work performed by the flow against canopy drag ensures that turbulence moments diminish rapidly with descent into the canopy, similar to that found in the vicinity of numerous other canopies (e.g. Raupach Reference Raupach1994). On the windward side of the hills ( $x/L \sim -1$ ), $\sigma _u/u_*$ and $\sigma _w/u_*$ change little at canopy top with the increased streamwise velocity increases shown in figures 8 and 9, however, the decreased vertical gradient in the streamwise wind at this $x/L$ does manifest in reduced momentum stress in the canopy’s vicinity – with a greater amplitude reduction of $\langle u'w' \rangle / u_*^2$ near canopy-top in the cases with 3D hills compared with 2D hills sufficient to create a $\langle u'w' \rangle / u_*^2$ minimum just above the canopy. The steeper hills ( $s_m = 0.26$ ) also reveal a very small region of weak near-surface upward turbulent momentum flux beneath canopy-top driven by the thrust force found in this region (figure 13). At hill-crest ( $x/L = 0$ ), increased vertical shear of streamwise velocity amplifies $\sigma _u/u_*$ and $\langle u'w' \rangle / u_*^2$ compared with their upstream values at $x/L = -4$ , while $\sigma _w/u_*$ diminishes slightly. On the hill’s leeward side ( $x/L = 1$ and $x/L = 2$ ), the hill- and canopy-induced adverse pressure gradient reduces mean streamwise velocity producing enhanced shear up to at least $z/h_c = 4$ which amplifies all three second moments throughout this depth compared with their upstream values (figure 15). At $x/L = 1$ just above the canopy, $\sigma _u / u_*$ and $\langle u'w' \rangle / u_*^2$ increase most in the shallower hill cases ( $s_m = 0.16$ ) where the flow does not separate no matter the hill shape. Within the broader hill-induced shear layer in the hill lee, flow over 2D hills amplifies $\sigma _w / u_*$ and $\langle u'w' \rangle / u_*^2$ more-so than over 3D hills as the turbulence acts to counter the adverse pressure gradient. By $x/L = 4$ , $\sigma _u / u_*$ has nearly recovered its upstream profile, but not $\sigma _w / u_*$ and $\langle u'w' \rangle / u_*^2$ – especially for cases with steeper hills ( $s_m = 0.26$ ).

To elaborate on a 3D hill’s influence on turbulence, figure 16 presents the spatial variation of turbulence moments along a constant $\zeta$ -surface at canopy top in the steeper ( $s_m = 0.26$ ) 3D-hill simulation. On the windward side, pressure gradients induced by the steeper ( $s_m = 0.26$ ) 3D hills enhance $\sigma _u$ (primarily between $-1 \lesssim x/L \lesssim 0$ and $-1 \lesssim y/L \lesssim 1$ ), enhance $\sigma _v$ more broadly spatially across the hill, and slightly diminish $\sigma _w$ (in a similar spatial region as $\sigma _u$ ). On the leeward side of the steep 3D hills: (i) $\sigma _u$ rapidly diminishes to magnitudes below upstream values over a similar range of $y/L$ ( $-1 \lesssim y/L \lesssim 1$ ) but extending to at least $x/L = 6$ ; (ii) $\sigma _v$ diminishes below upwind values over most of the hill’s leeward region, but then picks up again when the terrain flattens; (iii) $\sigma _w$ increases throughout the leeward hill region peaking at the hill base and then slowly returns to upstream values by approximately $x/L = 4$ .

Figure 16.

Horizontal slices of time-averaged velocity standard deviations normalized by $u_*$ (a–c) and momentum flux normalized by $u_*^2$ (d–f) along the $\zeta /h_c = 0.95$ surface (i.e. near canopy top) from the steeper ( $s_m = 0.26$ ) 3D hill simulation, 3D–0.26. In (a)–(c), results are presented for streamwise velocity, $\sigma _u$ (a,d), spanwise velocity, $\sigma _v$ (b,e), and vertical velocity, $\sigma _w$ (c,f), and in (d)–(f) results are presented for vertical flux of streamwise momentum, $\langle u'w' \rangle$ (d), vertical flux of spanwise momentum, $\langle v'w' \rangle$ (e), and spanwise flux of streamwise momentum, $\langle u'v' \rangle$ (f). The dashed black line depicts the location of the hill base at $\zeta /L = 0$ , and the black cross marks the hill-crest. The mean wind flow is from left to right (in the $+x$ direction).

Steep 3D hills ( $s_m = 0.26$ ) reduce the vertical flux of streamwise momentum at canopy-top across their entire windward side, with peak reductions down to as low as $\langle u'w' \rangle /u_*^2 \sim 0.1$ between $-1 \lesssim x/L \lesssim 0$ and $-1 \lesssim y/L \lesssim 1$ , i.e. the region coincident with the largest positive hill-induced streamwise pressure gradient (figure 12 e). Steep 3D hills ( $s_m = 0.26$ ) accentuate $\langle u'w' \rangle /u_*^2$ at canopy-top primarily on the outward flanks (between $0.5 \lesssim x/L \lesssim 2$ and $0.5 \lesssim \pm y/L \lesssim 1.5$ ). Vertical shear of the spanwise wind (figure 10) driven by the hill-induced pressure gradient ensures an importance of canopy-top vertical flux of spanwise momentum ( $\langle v'w' \rangle /u_*^2$ ) on the outer flanks of the hill, with peaks between $-1 \lesssim x/L \lesssim 0$ and $0.5 \lesssim \pm y/L \lesssim 1.5$ , however, the hill-induced peaks of $\langle v'w' \rangle /u_*^2$ are of notably smaller magnitude than the hill-induced modification to $\langle u'w' \rangle /u_*^2$ . Flow divergence around the windward side of the hill produces a spanwise flux of streamwise momentum ( $\langle u'v' \rangle /u_*^2$ ). More importantly, large-amplitude spanwise fluxes of streamwise momentum in the hill’s lee participate strongly in laterally transporting streamwise momentum leaking around the hill-sides to regions inward behind hill-crest– a flow recovery mechanism not present in flow over 2D hills. The variability in figure 16 highlights limitations of the finite duration time-averaging in the 3D-hill cases.

7. Evaluating current theory

The small perturbation theory outlined in § 2 was originally developed for predicting turbulence over very low hills but is frequently applied outside its strict range of validity. The present LES data provide an opportunity to evaluate the analytic theory when applied to flows in Regime 4. Here, we evaluate how well results on the 2D ridges and on the plane of symmetry of the 3D hills follow the analytic theory.

7.1. Perturbation analysis description

7.1.1. Turbulence production terms in streamline coordinates

Current theory describing turbulent flow over forested hills hinges on equations written in streamline coordinates that simplify interpretation of the hill-induced forces perturbing the flow (e.g. Finnigan & Belcher Reference Finnigan and Belcher2004). The dominant production terms in the 2D Reynolds stress equations valid for the LES along hill-centreline in streamline coordinates can be written as

(7.1) \begin{align} \tilde {u}\, \frac {\partial \, \langle \tilde {u}'\tilde {w}'\rangle }{\partial \tilde {x}} &= \,-\,\sigma _{\tilde {w}}^2 \, \frac {\partial \tilde {u}}{\partial \tilde {z}} - \frac {1}{2} \langle \tilde {u}'\tilde {w}'\rangle \frac {\partial \tilde {u}}{\partial \tilde {x}} - \left ( 2 \sigma _{\tilde {u}}^2 - \sigma _{\tilde {w}}^2 \right ) \frac {\tilde {u}}{R} + \boldsymbol{\cdots} ,\end{align}

(7.2) \begin{align} \tilde {u}\, \frac {\partial \,\sigma _{\tilde {u}}^2}{ \partial \tilde {x}} &= - 2\,\sigma _{\tilde {u}}^2\, \frac {\partial \tilde {u}}{\partial \tilde {x}} - 2 \, \langle \tilde {u}'\tilde {w}'\rangle \, \frac {\partial \tilde {u}}{\partial \tilde {z}} + 2 \, \langle \tilde {u}'\tilde {w}'\rangle \, \frac {\tilde {u}}{R} + \boldsymbol{\cdots} ,\end{align}

(7.3) \begin{align} \tilde {u}\, \frac {\partial \,\sigma _{\tilde {w}}^2}{ \partial \tilde {x}} &= \,\,\,2\,\sigma _{\tilde {w}}^2 \,\frac {\partial \tilde {u}}{\partial \tilde {x}} - 4\, \langle \tilde {u}'\tilde {w}'\rangle \, \frac {\tilde {u}}{R} + \boldsymbol{\cdots} ,\end{align}

where, the ellipses represent the triple moment, SGS, and canopy drag terms and the $\langle \phantom {\,}\rangle$ averaging notation is only retained for the covariances. Note that in (7.1) to (7.3) the sign convention applied to the streamline curvature $1/R$ is opposite to that used in Finnigan (Reference Finnigan1983) and Kaimal & Finnigan (Reference Kaimal and Finnigan1994). As in Finnigan (Reference Finnigan2024), we define $R$ or $1/R$ as negative if the centre of curvature lies in the negative $z$ direction (Aris Reference Aris1990). In (7.1) to (7.3), the operators ( $\partial /\partial \tilde {x}$ , $\partial /\partial \tilde {z}$ ) denote directional derivatives parallel and perpendicular to the ( $\tilde {x}$ , $\tilde {z}$ ) coordinate lines, respectively. Velocity components ( $\tilde {u}$ , $\tilde {w}$ ) and turbulent stresses ( $\sigma _{\tilde {u}}^2$ , $\sigma _{\tilde {w}}^2$ , $\langle \tilde {u}' \tilde {w}' \rangle$ ) in (7.1) to (7.3) should be interpreted as those that would be measured in a right-handed Cartesian coordinate frame ( $\tilde {x}$ , $\tilde {z}$ ) aligned at any point with its $\tilde {x}$ -axis tangent to the streamline and its $\tilde {z}$ -axis normal to the streamline. This coordinate system has the advantage that velocity vectors and tensors have their usual dimensions and interpretation but comes at the cost that partial derivatives must be replaced by directional derivatives (Finnigan Reference Finnigan2024).

7.1.2. Production terms in terrain-following coordinates

Flow separation complicates the use of streamline coordinates. We therefore turn to a coordinate system tied with the terrain-following coordinate surfaces of the simulation which remain well-defined even in the presence of flow separation. Upwind of any flow separation, we expect that the terrain-following coordinate lines do not depart very far from streamlines.

As an approximation to flow variables transformed into streamline coordinates in (7.1) to (7.3), we transform the LES flow variables into a system defined relative to the local tangent of the coordinate surfaces, i.e. we approximate $\tilde {u}$ and $\tilde {w}$ as

(7.4) \begin{align} \tilde {u} &\approx \phantom {-}u\,e_1 + w\,e_3, \,\,\,\,\text{and} \end{align}

(7.5) \begin{align} \tilde {w} &\approx -u\,e_3 + w\,e_1. \end{align}

where, $e_1 = {\rm d}x/({\rm d}x^2 + {\rm d}z ^2)^{( {1}/{2})}$ and $e_3 = {\rm d}z/({\rm d}x^2 + {\rm d}z^2)^{({1}/{2})}$ .

Turbulence statistics of variables in this terrain-following coordinate system ( $\langle \tilde {u}'\tilde {w}' \rangle$ , $\sigma _{\tilde {u}}^2$ , $\sigma _{\tilde {w}}^2$ ) are approximated by locally rotating time-averaged statistics of LES-derived variables calculated during the simulations into the terrain-following coordinate system via

(7.6) \begin{align} \langle \tilde {u}'\tilde {w}' \rangle &\approx - \sigma _u^2 e_1e_3 + \langle u'w' \rangle (e_1^2 - e_3^2) + \sigma _w^2 e_1e_3, \end{align}

(7.7) \begin{align} \sigma _{\tilde {u}}^2 &\approx \sigma _u^2 e_1^2 + 2 \langle u'w' \rangle e_1 e_3 + \sigma _w^2 e_3^2,\end{align}

(7.8) \begin{align} \sigma _{\tilde {w}}^2 &\approx \sigma _u^2 e_3^2 - 2 \langle u'w' \rangle e_1 e_3 + \sigma _w^2 e_1^2 .\end{align}

The directional derivatives ( $\partial /\partial \tilde {x}$ , $\partial /\partial \tilde {z}$ ) in (7.1) to (7.3) are approximated by derivatives along the LES coordinate surfaces (i.e. $\partial /\partial \tilde {x} \approx \partial / \partial \xi = \partial / \partial x$ , and $\partial /\partial \tilde {z} \approx \partial / \partial \zeta$ ), where we have taken advantage of the fact that $\xi = x$ (and ${\rm d}\xi = {\rm d}x$ ) in our code. An incremental arclength along a terrain-following coordinate line ${\rm d}\tilde {x} \approx {\rm d}x(1 + s^2)^{({ {1}/{2}})}$ , where $s = {\rm d}z/{\rm d}x$ is the local slope of the coordinate line. We additionally assume ${\rm d}\tilde {x} \approx {\rm d}x$ and recognize that the maximum slope $s_m$ of any terrain-following coordinate line in our simulations is 0.26 and that this choice introduces a small error in the derivatives of $\lesssim$ 3.3 %.

7.1.3. Analysis heights

We investigate the relationship between the changes to the mean flow and the Reynolds stresses in three layers: (i) the upper canopy layer $h_c \gt z \gt d$ (where $d$ is the canopy’s displacement height, Appendix B); (ii) the inner shear stress layer $\widehat {h_i} \gt z \gt h_c$ ; (iii) the middle layer $\widehat {h_m} \gt z \gt \widehat {h_i}$ . We therefore present variations of the mean flow and turbulence along lines of constant $\zeta$ midway through the middle layer at $\zeta _m = \widehat {h_i} + 0.5(\widehat {h_m} - \widehat {h_i})$ , midway through the inner surface layer at $\zeta _i = h_c + 0.5(\widehat {h_i} - h_c)$ and in the upper canopy at $\zeta _c = 0.75h_c$ . Since the middle layer and inner layer depths depend on the hill length scale $L$ (see § 3 and Appendix B), $\zeta _i$ and $\zeta _m$ change with hill steepness. Upwind of any flow separation, the terrain-following coordinate lines, $\zeta _m$ , $\zeta _i$ , $\zeta _c$ do not depart too far from streamlines.

Figure 17.

Streamwise variation of hill-induced perturbations of mean first- and second-order statistics relative to background values in the undisturbed flow upwind of the isolated hills (marked as $_b$ ) along the three constant $\zeta$ -coordinate surfaces: (a) middle-layer, $\zeta _m$ ; (b) inner-layer, $\zeta _i$ ; (c) upper canopy layer, $\zeta _c$ ; see § 7.1.3 for the definition of $\zeta _m$ , $\zeta _i$ and $\zeta _c$ . Panels (i) present perturbation streamwise velocity ( $\Delta \tilde {u}/u_b = ( \langle \tilde {u} \rangle - u_b )/u_b$ , where $u_b = \langle \tilde {u} \rangle _b$ ). Panels (ii) depict the variation of the centrifugal acceleration $\tilde {u}/R$ (in units of s $^{-1}$ ). Panels (iii) show $\partial \tilde {u} / \partial \tilde {x} = \partial \Delta \tilde {u} / \partial \tilde {x}$ (in units of s $^{-1}$ ). Panels (iv) present the perturbation vertical gradient of streamwise velocity $\partial \Delta \tilde {u} / \partial \tilde {z}$ . Panels (v) present perturbation streamwise momentum stress ( $\Delta \tilde {u}\tilde {w} / uw_b = ( \langle \tilde {u}'\tilde {w}' \rangle - uw_b ) / uw_b$ , where $uw_b = \langle \tilde {u}'\tilde {w}' \rangle _b$ ). Panels (vi) present perturbation streamwise velocity variance ( $\Delta \sigma ^2_{\tilde {u}} / \sigma ^2_{u_b} = ( \sigma ^2_u - \sigma ^2_{u_b}) / \sigma ^2_{u_b}$ , where $\sigma ^2_{u_b} = \langle \tilde {u}'^2 \rangle _b$ ), and panels (vii) present vertical velocity variance ( $\Delta \sigma ^2_{\tilde {w}} / \sigma ^2_{w_b} = ( \sigma ^2_{\tilde {w}} - \sigma ^2_{w_b}) / \sigma ^2_{w_b}$ , where $\sigma ^2_{w_b} = \langle \tilde {w}'^2 \rangle _b$ ). Long-dashed lines present results for cases with isolated 2D hills, and solid lines present results for cases with 3D hills along hill-centreline; blue colours, $s_m = 0.16$ ; green colours, $s_m = 0.26$ . A 1-2-1 smoothing in the streamwise direction has been applied to all fields. The mean wind flow is from left to right (in the $+x$ direction). See Appendix A for description of quantities marked with $_b$ .

8. Summary and conclusions

To advance understanding of the hill-slope’s and hill-shape’s role on turbulent air flow over isolated forested hills, we interrogate four turbulence-resolving simulations. A spectrally friendly fringe-technique enables the use of periodic boundary conditions to simulate flow over isolated 2D and 3D hills of cosine shape. The simulations target recently conducted WT experiments that are configured to fall outside the regimes for which current theory applies.

First, simulation skill for flow over isolated 3D hills is demonstrated through matching the canopy and hill configuration with the recently conducted WT experiments and intercomparing results. Subsequently, response of the mean and turbulent flow components to 2D versus 3D hills along hill-centreline are discussed. Finally, a discussion of the phase and amplitude of spatially varying responses of flow over forested hills are evaluated. Our analysis provides insight into flow features induced by changes in hill shape and slope when in Regime 4, and to the mechanisms behind and locations where assumptions made when developing current theory fail towards advancing theory to regimes beyond Regime 1.

Key findings include the following.

1. (i) Flow over isolated 2D forested hills produces larger amplitude vertical motions on a hill’s windward and leeward faces and speed-up of the mean wind compared with that over isolated 3D forested hills at hill-centreline. At canopy top, maximum speed up $\texttt {max}(\Delta u/u_b)_{h_c}$ occurs at approximately $x/L = -0.3$ . A change in hill slope from $s_m = 0.16$ to 0.26 increases $\texttt {max}(\Delta u/u_b)_{h_c}$ by approximately 30 % for 2D hills and 34 % for 3D hills. Flow separation induced by the steeper $s_m = 0.26$ hills ensures that mean flow fields require notably longer distances downstream of the hill before full recovery (i.e. not until $6 \lesssim x/L \lesssim 8$ ).

2. (ii) 3D hills generate surface pressure minima over hill-crest that are nearly half the magnitude of those over 2D hills. The 3D hills influence the pressure field in the spanwise direction out to $y/L \sim \pm 3$ . Pressure gradients in the spanwise direction are smaller than in the streamwise direction, but the spanwise pressure gradients are of sufficient amplitude to overcome downward turbulent momentum transport into the canopy and drive mean uphill within-canopy flow on the hill flanks. The spatial region over which the hill-induced negative pressure drag acts increases with increasing hill steepness, however, the horizontal extent over which this thrust force acts decreases as the hills change from a 2D ridge to an axisymmetric 3D hill.

3. (iii) The perturbation analysis in § 7 suggests that the assumptions about the dominant flow dynamics embodied in partitioning the flow into an upper layer with an inviscid response to the hill’s pressure field, an inner layer where changes to the shear stress and the mean flow are strongly coupled and a canopy layer where the nonlinear treatment of velocity perturbations in the lower canopy affects flow throughout the layer are robust inasmuch as they lead to solid predictions of hill-induced perturbations to the mean flow. However, when we try to apply those assumptions to predict the evolution of the turbulent moments, we find they provide approximate explanations at best. This is especially true in the upper canopy, where additional canopy-induced physics affects the transfer of TKE between orthogonal velocity components.

The results presented only scratch at the surface of understanding how hill shape and steepness modulate turbulent flow over low hills covered with a shallow forest canopy (Regime 4 in the $L/L_c$ versus $h_c/L_c$ parameter space) and how well current theory predicts their interaction. In particular, this analysis focuses on neutrally stratified conditions; inclusion of buoyancy forces would likely alter the current findings substantially.