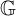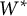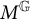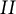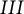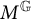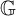1 Introduction
Recall [Reference Jones12, Proposition 2.1.4] that for any action of a finite group
${\mathbb G}$
on a von Neumann algebra M, the fixed-point subalgebra
$M^{{\mathbb G}}$
is or not of type I, II, III, or finite, along with M (i.e., these properties are equivalent for the two von Neumann algebras). The present note is aimed primarily at extending that result to its analog for actions of finite quantum groups
${\mathbb G}$
in the sense of [Reference Neshveyev and Tuset13, Definition 1.1.1]: unital
$C^*$
-algebras
$A:=C({\mathbb G})$
equipped with a unital
$C^*$
morphism
coassociative in the obvious sense and such that
$$ \begin{align*} \overline{(A\otimes {\mathbb C})\cdot \Delta A}^{\|\cdot\|} = A\otimes A = \overline{({\mathbb C}\otimes A)\cdot \Delta A}^{\|\cdot\|} \end{align*} $$
(products of sets meaning spans of products).
${\mathbb G}$
is finite when
$C({\mathbb G})$
is finite-dimensional, and actions on von Neumann algebras are as in [Reference Wang23, Definition 2.2]: writing
$L^{\infty }({\mathbb G})$
for the von Neumann closure of
$C({\mathbb G})$
in the GNS representation attached to the Haar state [Reference Neshveyev and Tuset13, Theorem 1.2.1]
$(A,h)$
, an action of
${\mathbb G}$
on M is a
$W^*$
morphism
such that
-
•
$(\operatorname {\mathrm {id}}\otimes \Delta )\circ \rho = (\rho \otimes \operatorname {\mathrm {id}})\circ \rho $
; -
• and
$$ \begin{align*} \overline{({\mathbb C}\otimes L^{\infty}({\mathbb G}))\cdot \rho M}^{W^*} = M\otimes L^{\infty}({\mathbb G}). \end{align*} $$
That in place, the quantum analog of the aforementioned [Reference Jones12, Proposition 2.1.4] reads the following.
Theorem 1.1. Let M be a
$W^*$
-algebra equipped with an action by a finite quantum group
${\mathbb G}$
. M and the fixed-point subalgebra
$M^{{\mathbb G}}$
then have the same canonical finite hyperfinite, atomic, diffuse, and type-
$\tau $
central projections for
$\tau \in \{I,\ II,\ III\}$
.
References for the various properties mentioned in the statement are provided in Example 2.3, and we refer to [Reference Takesaki21, Section V.1] for type-decomposition theory.
Theorem 1.1 follows fairly easily from work done in [Reference De Commer and Yamashita4] on finite-index expectations attached to quantum actions. A brief reminder on the various notions of finiteness introduced in [Reference Baillet, Denizeau and Havet1, Définition 3.6] for conditional expectations 
onto
$W^*$
-subalgebras (i.e., [Reference Blackadar2, Section II.6.10]
$\sigma $
-weakly continuous norm-1 idempotents) will help provide some context.
-
• E is of finite index if
$E-\lambda $
is completely positive [Reference Blackadar2, Section II.6.9] for some
$\lambda>0$
: (1-1)
$$ \begin{align} E(x^*x)\ge \lambda x^*x ,\quad \forall x\in M\otimes M_n \quad\text{for some fixed } \lambda>0 \text{ and arbitrary } n\in {\mathbb Z}_{>0}; \end{align} $$
Equivalently [Reference Frank and Kirchberg9, Theorem 1], it is enough to require (1-1) for
$n=1$
alone, i.e., the positivity of
$E-{\lambda }$
entails its complete positivity. In the language of [Reference Baillet, Denizeau and Havet1, Définition 3.6], being of finite index is equivalent to being weakly of finite index. -
• E is strongly of finite index if furthermore M, regarded as an M–N-correspondence [Reference Baillet, Denizeau and Havet1, Définition 2.1(i)] via E, has a finite orthonormal basis ([Reference Baillet, Denizeau and Havet1, Définition 1.6], [Reference Denizeau and Havet5, Section 1.1], and [Reference Paschke15, Theorem 3.12]; (complete) quasi-orthonormal system in [Reference Skeide19, Definitions 4.8 and 4.10 and Theorem 4.11]).
We will also substitute Pimsner–Popa or PP for the phrase of finite index, following [Reference Popa and Wassermann18, Section 2.1].
The proof of Theorem 1.1 follows a small detour meant to abstract away from the specifics of type decompositions and the like, proving that PP expectations preserve certain classes of von-Neumann-algebra properties of which being of type
$\tau \in \{I,\ II,\ III\}$
, or diffuse, or hyperfinite are examples.
Definition 1.2 Consider a
$W^*$
-algebra property
${\mathcal P}$
, transferred to projections
$p\in N$
by saying that p has (or is)
${\mathcal P}$
if
$pNp$
does (or is).
-
(1)
${\mathcal P}$
is ideal if for every von Neumann algebra N (1-2)is a (lattice-theoretic [Reference Blyth3, Definition post Example 2.15]) ideal:-
• closed under taking suprema;
-
• and a down-set [Reference Blyth3, Definition post Example 1.13]:
-
-
(2)
${\mathcal P}$
is completely ideal if it is ideal and (1-2) is furthermore complete, i.e., closed under arbitrary suprema. -
(3)
${\mathcal P}$
is instead (only) Z-completely ideal if it is ideal and closed under centrally orthogonal [Reference Takesaki21, pre Theorem V.1.8] sums (i.e., sums of projections whose respective central supports [Reference Takesaki21, pre Corollary IV.5.6] are orthogonal).
Theorem 2.5 below shows that completely ideal properties travel well along PP expectations, Corollary 2.6 specializes this to the properties listed in Theorem 1.1, and the latter follows. A version of Theorem 2.5 applicable to strongly PP expectations and Z-completely ideal properties is proven in Theorem 2.7, and might be of some independent interest given the context.
2 Permanence under sufficiently non-degenerate expectations
Recall the Introduction’s finiteness expectation conditions.
Remark 2.1 One simple observation that it will be convenient to take for granted now and then is that being strongly PP is equivalent to being PP and M being finitely generated as a right N-module in the purely algebraic sense that
$$ \begin{align*} M=x_1N+\cdots+x_sN \quad\text{for some}\quad x_i\in M. \end{align*} $$
One direction is obvious; as for the other (
$\Leftarrow $
), note that in general, an N–
$W^*$
-module X finitely generated as plain N-module has a finite orthonormal basis. One can induct on the number s of generators:
-
•
can be assumed a projection after polar-decomposing the original
$x_1$
[Reference Paschke15, Proposition 3.11]; -
• this then gives a projection
in
${\mathcal L}_N(X)$
;
-
• and the summand
$(1-Q)X\le X$
complementary to
$QX$
is generated by the (images of the)
$s-1$
elements
$x_j$
,
$2\le j\le s$
, propelling the induction.
can be assumed a projection after polar-decomposing the original 
A few simple preliminary remarks, useful enough to set out explicitly, but left as an exercise (in abstracting away from, say, [Reference Takesaki21, Theorem V.1.19]).
Lemma 2.2. Let N be a von Neumann algebra and
${\mathcal P}$
a
$W^*$
-algebra property.
-
(1) If
${\mathcal P}$
is completely ideal the strong negation
${\mathcal P}'$
of
${\mathcal P}$
defined by is also completely ideal, and
$z_{N,{\mathcal P}'}=1-z_{N,{\mathcal P}}$
.
-
(2) If
${\mathcal P}$
is completely ideal there is a largest
${\mathcal P}$
-projection
$z_{N,{\mathcal P}}\in N$
, automatically central. -
(3) If
${\mathcal P}$
is only Z-completely ideal the Z-strong negation of
${\mathcal P}$
is closed under arbitrary suprema.
-
(4) If
${\mathcal P}$
is Z-completely ideal then there still is a largest central
${\mathcal P}$
-projection
$z=z_{N,{\mathcal P}}\in N$
, and
$1-z$
is the largest
${\mathcal P}_Z'$
-projection.
Examples 2.3
-
(1) The property of being type
$\tau \in \{I,\ II,\ III\}$
is completely ideal, as follows from downward closure [Reference Dixmier6, Proposition 11 and Corollary 4 to Proposition 13 of Section I.6.8; Proposition 4 of Section I.8.3] and the central decomposition [Reference Takesaki21, Theorem V.1.19]
$1=z_I+z_{II}+z_{III}$
. -
(2) Recall (see [Reference Blackadar2, Section IV.2.2.1] and [Reference Strătilă20, Section 10.21]) that a
$W^*$
-algebra is atomic if every nonzero projection dominates a minimal nonzero projection. Atomicity is completely ideal, with closure under suprema following from the general discussion on the relative position of two projections in [Reference Takesaki21, discussion preceding Theorem V.1.41].The strong negation of atomicity is diffuseness (see [Reference Strătilă20, Section 29.2] and [Reference Blackadar2, Theorem III.4.8.8]); it too is completely ideal, either as a direct simple exercise or by Lemma 2.2(1).
-
(3) Another completely ideal property is that of being AFD (short for approximately finite-dimensional [Reference Takesaki22, Definition XIV.2.3] and an alternative for hyperfinite, following [Reference Elliott and Woods7, p. 175]). It means that arbitrary finite subsets of the von Neumann algebra in question (N, say) are arbitrarily approximable in the
$\sigma $
-strong
$^*$
topology [Reference Blackadar2, Section I.3.1.6] by finite-dimensional von Neumann subalgebras, and is equivalent (see [Reference Elliott8, Theorem 2 and Corollary 5] and [Reference Haagerup10, Section 6.4]) to the injectivity [Reference Blackadar2, Section IV.2.2] of N.As to the fact that AFD-ness is completely ideal:
-
• Closure under projection cutting is noted in [Reference Blackadar2, Example IV.2.1.2(iii)].
-
• For AFD projections
$p,q\in N$
, the supremum
$p\vee q$
is again AFD:-
– the already-mentioned relative-position analysis of [Reference Takesaki21, discussion preceding Theorem V.1.41] will afford a decomposition
with all
$$ \begin{align*} (p\vee q)N(p\vee q) \cong N_0\otimes M_2 \times \prod_{i=1}^4 N_i \end{align*} $$
$N_i$
projection cuts of either
$pNp$
or
$qNq$
and hence AFD by the preceding point;
-
– while tensoring with finite-dimensional
$W^*$
-algebras and finite products preserve the AFD property by [Reference Blackadar2, Corollary IV.2.1.5 and Example IV.2.1.2(ii)], respectively.
-
-
• Finally, closure under filtered inclusions of AFD subalgebras is self-evident from the very definition of approximate finite-dimensionality, hence closure under arbitrary suprema.
-
-
(4) One example of a commonly-discussed property that of course is not completely ideal is finiteness: for infinite-dimensional H, the identity of
${\mathcal L}(H)$
is the supremum of finite-rank (hence finite) projections. Finiteness is ideal though [Reference Takesaki21, Theorem V.1.37], and in fact [Reference Takesaki21, Lemma V.1.18] Z-completely so. -
(5) Proper infinitude [Reference Takesaki21, Definition V.1.15], on the other hand, is not ideal (let alone completely or Z-completely so) because it is not closed under projection-cutting: the same example
$N:={\mathcal L}(H)$
above is properly infinite (i.e., its nonzero projections are all infinite), but
$pNp$
is finite for finite-rank p.Note in passing that proper infinitude is precisely the Z-strong negation of finiteness in the sense of Lemma 2.2(4).
Remark 2.4 Lemma 2.2(4) is intended precisely as stated: for Z-completely ideal
${\mathcal P} z_{N,{\mathcal P}}$
is by definition the largest central
${\mathcal P}$
-projection in N, while its complement
$z_{N,{\mathcal P}_Z'}=1-z_{N,{\mathcal P}}$
is the largest
${\mathcal P}_Z'$
-projection period, central or not.
For illustration, consider Examples 2.3(4) and 2.3(5) above: in the central decomposition
of [Reference Takesaki21, Theorem V.1.19] the second central summand
$z'$
dominates every properly infinite projection in N.
Theorem 2.5. Let 
be a PP conditional expectation and
${\mathcal P}$
a completely ideal property that descends along such expectations. The maximal central projections
$z_{N,{\mathcal P}}$
and
$z_{M,{\mathcal P}}$
then coincide.
Proof Under the PP assumption we also have [Reference Baillet, Denizeau and Havet1, Théorème 3.5, Lemme 2.15, and Section 3.10] a PP expectation 
from the von Neumann algebra [Reference Paschke15, Proposition 3.10] of adjointable continuous N-module endomorphisms of the M–N-correspondence (hence also a right N-
$W^*$
-module) attached [Reference Baillet, Denizeau and Havet1, Proposition 2.8] to the expectation E.
Note furthermore that
$X_E$
is non-degenerate [Reference Denizeau and Havet5, Section 1.1] as an N-
$W^*$
-module: the ideal of N generated by 
,
$x,y\in X_E$
is (dense in) N.
-
(I) :
${\mathcal P}$
or its absence are equivalent for N and
${\mathcal L}_N(X_E)$
. This is true of N and
${\mathcal L}_N(X)$
for any non-degenerate N-
$W^*$
-module X: by the general structure [Reference Paschke15, Theorem 3.12] we have
$$ \begin{align*} {\mathcal L}_N(X)\cong p \left(N\otimes{\mathcal L}(\ell^{2}(S))\right)p ,\quad S\text{ a set and } p\in N\otimes{\mathcal L}(\ell^{2}(S))\text{ a projection}. \end{align*} $$
Indeed, if
$(x_s)_{s\in S}$
is an orthonormal basis for X (what [Reference Paschke15, Theorem 3.12] provides) with corresponding projections , then (2-1)
$$ \begin{align} X\cong \bigoplus_{s\in S} p_s N \quad\text{and}\quad {\mathcal L}_N(X) = p \left(N\otimes{\mathcal L}(\ell^{2}(S))\right)p \quad\text{with}\quad p:=\mathrm{diag}\left(p_s,\ s\in S\right). \end{align} $$
The operations of projection-cutting (i.e.,
$\bullet \mapsto p\bullet p$
) and tensoring with a type-I factor both preserve completely ideal properties, transporting
${\mathcal P}$
from N to
${\mathcal L}_N(X)$
. Conversely, if the latter has property
${\mathcal P}$
then so do its corners
$p_sNp_s$
and non-degeneracy means that
$\bigvee _s p_s=1\in N$
, hence the claim. -
(II) :
${\mathcal P}$
lifts from N to M. For it lifts from N to
${\mathcal L}_N(X_E)$
by (I), and then descends to M along
$E_1$
by hypothesis. -
(III) : The strong negation
${\mathcal P}'$
descends along PP expectations. Suppose N is not
${\mathcal P}'$
, i.e.,
$z_{N,{\mathcal P}}\ne 0$
. (II) applied to then implies that the nonzero
$W^*$
-algebra
$z_{N,{\mathcal P}}Mz_{N,{\mathcal P}}$
is
${\mathcal P}$
, negating
${\mathcal P}'$
for M.
-
(IV) : The strong negation
${\mathcal P}'$
lifts from N to M. Consider the central decomposition
$1=z_{M,{\mathcal P}}+z_{M,{\mathcal P}'}$
of Lemma 2.2(1). We have [Reference Baillet, Denizeau and Havet1, Section 3.9] a PP expectation (2-2)and the
${\mathcal P}'$
property for N (hence also for
$zN$
) entails it for
$zM$
by (II) applied to
${\mathcal P}'$
(completely ideal again by Lemma 2.2(1) and still descending along PP expectations by (III)).
$z=z_{M,{\mathcal P}}$
thus vanishes, i.e., the target rephrased.
-
(V) : Conclusion. Applying (II) and (IV) to the expectations
respectively, we obtain an orthogonal decomposition
$1=z_{N,{\mathcal P}}+z_{N,{\mathcal P}'}$
into a
${\mathcal P}$
and a
${\mathcal P}'$
summand. Now,
$z:=z_{N,{\mathcal P}}$
and
$z':=z_{N,{\mathcal P}'}$
cannot have nonzero sub-projections for then
$$ \begin{align*} p\le z \quad\text{and}\quad p'\le z' \quad\text{equivalent in }M, \end{align*} $$
$pMp\cong p'Mp'$
would be both
${\mathcal P}$
and non-
${\mathcal P}$
. It follows [Reference Takesaki21, Lemma V.1.7] that z and
$z'$
are centrally orthogonal in M. Being themselves orthogonal and complementary, z and
$z'$
must also be central in M, so that
$1=z+z'$
is the canonical central decomposition of M attached to property
${\mathcal P}$
.
, then 
[Reference Popa and Wassermann18, Section 2.1] (essentially) claims, and [Reference Frank and Kirchberg9, Propositions 2.1 and 2.2] imply Corollary 2.6 (give or take, minus the AFD property) for PP expectations.
Corollary 2.6. If there is a PP conditional expectation 
, then the maximal central projections
-
(a)
$z_{\tau }$
of respective types
$\tau \in \{I,\ II,\ III\}$
, -
(b)
$z_a$
(atomic), -
(c)
$z_d$
(diffuse), -
(d) and
$z_{AFD}$
(AFD),
for M and N coincide.
Proof Given that diffuseness and type
$III$
are the respective strong negations of atomicity and semifiniteness [Reference Blackadar2, Sections III.1.4.2 and III.1.4.7], the claims are all direct consequences of Theorem 2.5 once we recall that
-
• semifiniteness [Reference Blackadar2, Corollary III.2.5.25(i)]
-
• being of type I [Reference Blackadar2, Theorem III.2.5.26] (or discrete [Reference Blackadar2, Section III.1.4.4]),
-
• atomicity [Reference Blackadar2, Theorem IV.2.2.3]
-
• and AFD-ness (obviously by [Reference Blackadar2, Proposition IV.2.1.4] and the equivalence [Reference Elliott8, Theorem 2 and Corollary 5] AFD
$\Leftrightarrow $
injective),
all descend along arbitrary (not just PP) conditional expectations.
[Reference Jolissaint11, Théorème 2.2(1)] shows that finiteness lifts along strongly PP expectations. [Reference Popa17, Property 1.1.2(iii)] makes the parallel claim under only the weak PP assumption, while [Reference Parshall and Wang14, Section 2.1] amplifies that claim with the assertion that the finite/properly infinite central decompositions of M and N coincide in the presence of a weakly PP expectation. The weaker version assuming strong PP-ness (strengthening [Reference Jolissaint11, Théorème 2.2(1)]) can be recovered by specializing Theorem 2.7 below to
${\mathcal P}$
= finiteness (per Example 2.3(4)).
Theorem 2.7. Let 
be a strongly PP conditional expectation and
${\mathcal P}$
a Z-completely ideal property that descends along such expectations. The central decompositions
$$ \begin{align*} z_{N,{\mathcal P}} + z_{N,{\mathcal P}_Z'} = 1 = z_{M,{\mathcal P}} + z_{M,{\mathcal P}_Z'} \end{align*} $$
of Lemma 2.2(4) coincide.
Proof The proof plan roughly follows that of Theorem 2.5, with appropriate modifications.
-
(I) :
${\mathcal P}$
is equivalent for N and
${\mathcal L}_N(X_E)$
. Precisely as in part (I) of Theorem 2.5, with the S of (2-1) finite this time around.Section (II) of the proof of Theorem 2.5 now also applies to yield its respective analog.
-
(II) :
${\mathcal P}$
lifts from N to M.The counterpart to section (IV) of the earlier proof, on the other hand, is easily verified directly.
-
(III) : The Z -strong negation
${\mathcal P}_Z'$
lifts from N to M. If M were to contain a nonzero central
${\mathcal P}$
-projection z, the induced expectation (2-2) would ensure by the descent assumption that the nonzero quotient
$N\to zN$
of N is
${\mathcal P}$
. This amounts to a nonzero central
${\mathcal P}$
-projection for N, contradicting
${\mathcal P}^{\prime }_Z$
. -
(IV) : Conclusion. We now have a decomposition
$1=z_{N,{\mathcal P}}+z_{N,{\mathcal P}_Z'}$
in M, and we will be done as soon as we argue that
$z_{N,{\mathcal P}_Z'}\in M$
is central.Observe first that liftability (step (III)) applied in the context of the (still strong PP) expectation
(2-3)induced by E via [Reference Baillet, Denizeau and Havet1, Section 3.9] in particular implies thatwhat we have to rule out is the possibility that this domination be strict. To that end, consider the
${\mathcal P}$
version of (2-3) and conclude via (II) that the central
${\mathcal P}$
-projection
$z_{M,{\mathcal P}}\le z_{N,{\mathcal P}}$
of
$z_{N,{\mathcal P}}Mz_{N,{\mathcal P}}$
cannot be strictly smaller than the unit
$z_{N,{\mathcal P}}\in z_{N,{\mathcal P}}Mz_{N,{\mathcal P}}$
.
Proof of Theorem 1.1
Consider the spectral projections
onto the respective isotypic subspaces ([Reference Podleś16, Theorem 1.5] or [Reference De Commer and Yamashita4, Section 2.2]). In particular, we have a conditional expectation
The conclusion is a direct application of Corollary 2.6 for all but finiteness and [Reference Frank and Kirchberg9, Proposition 2.1] for the latter, as soon as we verify that E is PP. Now, [Reference De Commer and Yamashita4, Lemma 2.5] proves a “local” version of the desired result, valid for arbitrary compact quantum
${\mathbb G}$
: for every
$\alpha \in \operatorname {\mathrm {Irr}} {\mathbb G}$
there is some
$\lambda _{\alpha }>0$
with
$$ \begin{align} E(x^*x)\ge \lambda_{\alpha} E_{\alpha}(x)^*E_{\alpha}(x)\ \text{matricially} ,\quad \forall x\in M. \end{align} $$
Assuming (as we are) that
${\mathbb G}$
is finite and hence
$\left |\operatorname {\mathrm {Irr}}({\mathbb G})\right |<\infty $
, for every
$x\in M$
, we have
$$ \begin{align*} \begin{aligned} x^*x &= \left(\sum_{\alpha} E_{\alpha}(x)^*\right) \left(\sum_{\alpha} E_{\alpha}(x)\right)\\ &\le |{\mathrm{Irr}}({\mathbb G})|^2 \sum_{\alpha} E_{\alpha}(x)^* E_{\alpha}(x) \quad \text{by } \textit{Cauchy Schwartz}\ [{2}\ \S{\rm I}.1.1.2]\\ &\le |{\mathrm{Irr}}({\mathbb G})|^2\left(\max_{\alpha}\frac 1{\lambda_{\alpha}}\right) E(x^*x) \quad\text{by (2-4)}, \end{aligned} \end{align*} $$
all valid matricially. (1-1) thus holds for
$$ \begin{align*} \lambda := \frac{1}{|\operatorname{\mathrm{Irr}}{\mathbb G}|^2}\min_{\alpha}\lambda_{\alpha}, \end{align*} $$
and we are done.
Acknowledgements
I am grateful for instructive comments from K. De Commer, A. Freslon, P. Sołtan, M. Wasilewski and M. Yamashita, as well as the anonymous referee’s insightful comments and suggestions.
Open access
