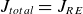1. Introduction
Major disruptions of tokamak fusion plasmas pose a significant risk to the integrity of fusion devices due to large electromagnetic forces, thermal heat loads and in particular large runaway electron (RE)-induced heat loads given the potential generation of large quantities of REs (Breizman et al. Reference Breizman, Aleynikov, Hollmann and Lehnen2019). In high-current devices, a RE avalanche can rapidly develop after a thermal quench due to the strong inductive electric field (Martín-Solís et al. Reference Martín-Solís, Sánchez and Esposito2010; Aleynikov & Breizman Reference Aleynikov and Breizman2015; Stahl et al. Reference Stahl, Hirvijoki, Decker, Embréus and Fülöp2015; Liu et al. Reference Liu2018; Svensson et al. Reference Svensson, Embreus, Newton, Särkimäki, Vallhagen and Fülöp2021). As a result, even a small initial population of REs can evolve into a substantial current carrier, specifically in high-current tokamaks where the avalanche amplification factor (Rosenbluth & Putvinski Reference Rosenbluth and Putvinski1997) is particularly high. Without effective mitigation strategies, these high-energy REs may ultimately impact a device’s first wall in a highly localised manner, posing a severe threat to its safe operation (Ratynskaia et al. Reference Ratynskaia2025).
To mitigate the risks associated with disruption consequences, several techniques have been applied in tokamak experiments, e.g. massive gas injection and shattered pellet injection (Lehnen et al. Reference Lehnen2015; Chen et al. Reference Chen2016; Nardon, Hu & Artola Reference Nardon2021; Tinguely et al. Reference Tinguely2021). In addition, a novel technique has been successfully applied in DIII-D experiments for real-time plasma stability monitoring, contributing to the prediction of disruption in the future (Liu et al. Reference Liu, Wang, Boyer, Munaretto, Wang, Park, Logan, Yang and Park2021b , Reference Liu, Munaretto, Logan, Wang, Boyer, Wang, Keith and Park2023). In view of such mitigation scenarios, three-dimensional (3-D) plasma instabilities and their interaction with REs play a key role. And also the so-called benign termination scenarios (Bandaru et al. Reference Bandaru, Hoelzl, Reux, Ficker, Silburn, Lehnen and Eidietis2021; Paz-Soldan et al. Reference Paz-Soldan2021; Reux et al. Reference Reux2021), which may offer drastically reduced heat loads, are highly dependent on the nature of plasma instabilities that cause the sudden loss of RE confinement. Experiments and simulations have demonstrated that REs can influence plasma instabilities (Cai & Fu Reference Cai and Fu2015; Bandaru et al. Reference Bandaru, Hoelzl, Reux, Ficker, Silburn, Lehnen and Eidietis2021; Liu et al. Reference Liu, Li, Kim, Lao and Parks2021c ; Sainterme & Sovinec Reference Sainterme and Sovinec2024) and excite kinetic instabilities (Fülöp et al. Reference Fülöp, Pokol, Helander and Lisak2006; Liu et al. Reference Liu2018; Spong et al. Reference Spong2018). Besides numerous experimental attempts to understand the underlying physics, also a number of different numerical models have been developed to simulate the complex interactions between REs and plasma instabilities during disruptions. One approach is to describe the dynamics of the relativistic REs in a simplified way as a distinct fluid population (Bandaru et al. Reference Bandaru, Hoelzl, Artola, Papp and Huijsmans2019; Zhao et al. Reference Zhao, Liu, Jardin and Ferraro2020a ; Liu et al. Reference Liu, Zhao and Jardin2021a , Reference Liu, Li, Kim, Lao and Parksc ) that self-consistently interacts with the bulk plasma. Such a fluid treatment has been incorporated into several codes, including the nonlinear magnetohydrodynamics (MHD) code JOREK (Bandaru et al. Reference Bandaru, Hoelzl, Artola, Papp and Huijsmans2019, Reference Bandaru, Hoelzl, Artola, Vallhagen and Lehnen2024), M3D-C1 (Liu et al. Reference Liu, Zhao and Jardin2021a ), MARS-F (Li et al. Reference Li, Liu, He, Wang, Guo and Zhong2021) and so on. The primary objective of these coupled simulations is to self-consistently capture the RE effect on the bulk plasma with a computationally reduced effort, providing insights into the mutual interactions during disruptive events. A hybrid approach combining particle-in-cell (PiC) methods with MHD has been employed to explore the influence of kinetic effects of REs (Bogaarts et al. Reference Bogaarts, Hoelzl, Huijsmans and Wang2022; Liu et al., Reference Liu, Jardin, Qin, Xiao, Ferraro and Breslau2022a ). Given the fact that REs might be highly relativistic, the curvature drift effect will play an important role, which either is ignored in the fluid treatment or can only be incorporated in a very simplified manner requiring additional assumptions regarding the RE phase-space distribution. Studies have indicated that this correction to the particle orbits can have a notable effect on the equilibrium and MHD behaviour (Bandaru & Hoelzl Reference Bandaru and Hoelzl2023). For high-fidelity modelling, both full-orbit (FO) (Bergström et al. Reference Bergström, Liu, Bandaru and Hoelzl2025) and guiding-centre (GC) (this work) equations have now been coupled to the MHD equations in JOREK, including relativistic and non-relativistic options. This article initially verifies the correctness of the model by comparisons regarding the axisymmetric equilibrium of a RE beam and the linear growth rate of tearing modes (TMs) in the presence of REs with analytical and numerical literature results in the fluid limit. Building on this foundation, it then turns towards a study of linear and nonlinear dynamics of TMs in a RE beam, taking into account the kinetic effects governing the interaction.
We aim at contributing to the understanding of MHD mode activity in RE beams, as it plays an important role, for instance in the development of benign RE beam termination scenarios that aim to avoid wall damage. Among various MHD instabilities, the classical TM (Furth, Rutherford & Selberg Reference Furth, Rutherford and Selberg1973; Hegna & Callen Reference Hegna and Callen1994) is particularly important in post-disruption plasmas with high resistivity, as it leads to the formation of magnetic islands through current-driven reconnection. Tearing mode signatures have also been directly observed in RE beams via synchrotron radiation diagnostics (Sommariva et al. Reference Sommariva2024). In Ohmic plasmas, TM evolution is well understood within the framework of resistive MHD. However, the presence of REs introduces additional complexities. While the post-disruption bulk plasma remains highly resistive, the nearly collisionless and relativistic nature of REs significantly modifies the reconnection dynamics (Cozzani Reference Cozzani2020). This modification affects both the linear stability of TMs and their nonlinear dynamics. The stochastic fields and islands can have a profound impact on the transport properties of REs (Martín-Solís et al. Reference Martín-Solís, Sánchez and Esposito1999), influencing their confinement and potential mitigation strategies. This study aims to investigate these interactions in detail, building upon prior work to elucidate the mechanisms governing the RE-driven modification of TMs. By improving our understanding of these processes, we can contribute to the development of more effective strategies for controlling RE beams in the future.
The rest of the article is structured as follows. In § 2, the hybrid fluid–kinetic model is introduced for which verification results are successively shown in § 3, where a two-dimensional benchmark was carried out regarding the major-radial force balance of a tokamak equilibrium with
$\boldsymbol{J}_{total}=\boldsymbol{J}_{RE}$
. Moreover, for validation regarding the 3-D physics, linear TM simulations in a RE beam were conducted, and the results were examined against analytical theory and other numerical approaches. Building upon this work, § 4 presents studies regarding the nonlinear TM dynamics in a RE beam with particular attention being paid to the saturated amplitude and the RE-driven magnetic reconnection process. Finally, § 5 concludes the article by summarising the work and providing a concise outlook to future work.
2. Hybrid fluid–kinetic model
Test particle methods can serve as an effective numerical approach for analysing the phase space and transport characteristics of energetic particles. Based on this method, numerous physical results have been obtained (del Castillo-Negrete et al. Reference del Castillo-Negrete, Carbajal, Spong and Izzo2018; Zhao et al. Reference Zhao, Wang and Wang2020b ; Liu et al. Reference Liu, Wang, Liu, Hu, Wu, Liu and Wang2022b , Reference Liu, Wang, Hu and Wang2024). This approach advances particle motion by time-dependent orbital equations, typically without solving the electromagnetic fields self-consistently. Generally, two types of orbital equations are employed: the GC equations and the FO Lorentz equations. From a computational perspective, the GC model is often more efficient, as it averages out the fast gyro-motion, reducing computational cost while preserving essential dynamics. In recent years, a test particle tracker has been implemented (Sommariva et al. Reference Sommariva, Nardon, Beyer, Hoelzl, Huijsmans and van Vugt2017; van Vugt et al. Reference van Vugt, Huijsmans, Hoelzl and Loarte2019) within the 3-D nonlinear MHD code JOREK (Huysmans & Czarny Reference Huysmans and Czarny2007; Hoelzl et al. Reference Hoelzl2021, Reference Hoelzl2024), enabling the computation of both FO and GC orbits. Conservation tests of key invariants have been conducted, and various applications have been explored (Sommariva et al. Reference Sommariva, Nardon, Beyer, Hoelzl and Huijsmans2018; Särkimäki et al. Reference Särkimäki, Artola and Hoelzl2022; Bergström et al. Reference Bergström, Särkimäki, Bandaru, Skyllas and Hoelzl2024). To advance this method to a self-consistent treatment of the RE mutual interaction with the background plasma, the FO kinetic REs were coupled to the fluid (Bergström et al. Reference Bergström, Liu, Bandaru and Hoelzl2025) following earlier work for supra-thermal ions (Bogaarts et al. Reference Bogaarts, Hoelzl, Huijsmans and Wang2022). With the present article, we introduce a drift-kinetic version of the hybrid fluid–kinetic model including verification via benchmarks and first nonlinear applications. In this framework, JOREK now evolves thermal particles through the corresponding fluid equations, while relativistic REs are treated kinetically using a full-f relativistic PiC technique (Bergström et al. Reference Bergström, Liu, Bandaru and Hoelzl2025).
The relativistic GC model implemented in JOREK follows the formulation described in Tao, Chan & Brizard (Reference Tao, Chan and Brizard2007):
\begin{eqnarray} \dot {\boldsymbol{X}}=\frac {p_\parallel ^\ast }{\gamma _r m_0}\frac {\boldsymbol{B}^\ast }{B_\parallel ^\ast }+\frac {\boldsymbol{b}}{ B_\parallel ^\ast }\ \times \left (p_\parallel \frac {\partial {\boldsymbol{b}}}{\partial t}-q\boldsymbol{E}+\frac {\mu }{\gamma _r}\boldsymbol{\nabla }B\right )\!,\nonumber \\ {\dot {p}}_\parallel =\frac {\boldsymbol{B}^\ast }{B_\parallel ^\ast }\boldsymbol{\cdot }\left (q\boldsymbol{E}-p_\parallel \frac {\partial {\boldsymbol{b}}}{\partial t}-\frac {\mu }{\gamma _r}\boldsymbol{\nabla }B\right )\!, \end{eqnarray}
where
\begin{align} B_\parallel ^\ast &=\boldsymbol{B}^\ast \boldsymbol{\cdot }\boldsymbol{b}\nonumber ,\\ \gamma _r&=\sqrt {1+\frac {p_\parallel ^2}{(m_0 c)^2}+\frac {2\mu B}{m_0 c^2}}, \end{align}
and
$\boldsymbol{X},\ p_\parallel \text{ and } \mu =p_\bot ^2/2 m_0 B$
represent the GC location, the momentum parallel to the magnetic field and the magnetic moment of the particle, respectively. Terms
$\boldsymbol{E}$
and
$\boldsymbol{B}$
denote the electric and magnetic fields, the effective magnetic field is given as
$\boldsymbol{B}^\ast =p_\parallel \boldsymbol{\nabla }\times \boldsymbol{b} +q \boldsymbol{B}$
, q is the charge,
$m_0$
is the rest mass of the particle,
$\boldsymbol{b}$
is the unit vector of the magnetic field and
$\gamma _r$
is the relativistic factor. The speed of light in vacuum is given by
$c$
. In terms of a numerical scheme, the fifth-order Cash–Karp Runge–Kutta method is applied for the GC pusher, and a volume-preserving algorithm is used for the FO pusher to ensure long-term accuracy. And a cylindrical coordinate system
$(R, Z, \phi )$
is used, where
$\phi$
denotes the toroidal angle. Particle locations are traced both in this global coordinate system as well as in the local finite-element coordinates. In terms of parallelisation, a hybrid MPI–OpenMP approach is used with the markers distributed over MPI ranks while a domain-cloning technique is used with respect to the finite-element fluid background simplifying load balancing and minimising communication overhead between the different MPI ranks.
In the GC formalism, the RE current consists of two components: the parallel current
$\boldsymbol{J}_{r,\parallel }$
associated with
$p_\parallel$
in (2.1) and the perpendicular current
$\boldsymbol{J}_{r,\perp }$
, which arises from GC drifts and the magnetisation current:
\begin{eqnarray} \boldsymbol{J}_{r,\perp } = \boldsymbol{J}_{r}^{\mathrm{drift}} + \boldsymbol{J}_{r}^{\mathrm{mag}}. \end{eqnarray}
The particle distribution in phase space is described by the function
$f(\boldsymbol{x}, \boldsymbol{v}, t)=\sum _{i=1}^{N} w_i \delta (\boldsymbol{x}_i(t))\delta (\boldsymbol{v}_i(t))$
, where
$w_i, \boldsymbol{x}_i, \boldsymbol{v}_i$
are the weight, position and velocity for the ith particle, and N is the total number of markers. In the hybrid model, the distribution is based on GC locations, and to account for finite gyro-radius effects, a four-point averaging method is planned in future work, but omitted here for simplicity. In this work, all markers are initialised with a pitch angle
$\xi = |p_\parallel /p| = 0.999$
, ensuring that a drift-kinetic treatment remains valid for investigating interactions between large-scale instabilities and REs.
The runaway current density is obtained by integrating the distribution function over velocity space, i.e.
$\boldsymbol{J}_r = -e \int \boldsymbol{v} f \, \text{d}^3v$
, and thus the drift current density is
\begin{eqnarray} \boldsymbol{J}_{r}^{\mathrm{drift}} = \sigma _r \frac {\boldsymbol{E} \times \boldsymbol{B}}{B^2} + \mathcal{P}_{r,\perp } \frac {\boldsymbol{B}\times \boldsymbol{\nabla }B}{B^3} - \mathcal{P}_{r,\parallel } \frac {\boldsymbol{\kappa }\times \boldsymbol{B}}{B^2}, \end{eqnarray}
where
$\sigma _r=-e n_r$
is RE charge density,
$\boldsymbol{\kappa }$
is the curvature of the magnetic field and the perpendicular and parallel pressures of REs are defined as
\begin{align} \mathcal{P}_{r,\perp } &=\frac {1}{2} \int \text{d}^3v \gamma _r m_0 v^2_\perp f, \nonumber \\ \mathcal{P}_{r,\parallel } &= \int \text{d}^3v \gamma _r m_0 v^2_{\parallel } f. \end{align}
The magnetisation current is the curl of magnetisation
$\boldsymbol{M}$
, which is the integration of magnetic moment
$\boldsymbol{\mu }$
. Here
$\boldsymbol{M}$
is given as
\begin{eqnarray} \boldsymbol{M} = \int \text{d}^3v \mu \boldsymbol{b} f = -\int \text{d}^3v \frac {\gamma _r m_0 v^2_\perp }{2B} f {\boldsymbol{b}} =-\frac {\mathcal{P}_{r,\perp }}{B}\boldsymbol{b}. \end{eqnarray}
We have the magnetisation current density:
\begin{eqnarray} \boldsymbol{J}_{r}^{\mathrm{mag}} = - \boldsymbol{\nabla }\times \left (\frac {\mathcal{P}_{r,\perp }}{B} {\boldsymbol{b}} \right ) = -\mathcal{P}_{r,\perp } \frac {\boldsymbol{B}\times \boldsymbol{\nabla }B}{B^3} + \mathcal{P}_{r,\perp } \frac {\kappa \times \boldsymbol{B}}{B^2} - \frac {1}{B}\left (\boldsymbol{\nabla }\mathcal{P}_{r,\perp } \times {\boldsymbol{b}}\right )\!. \end{eqnarray}
By summing the drift (2.4) and magnetisation (2.7) current components, the total perpendicular current can be defined as
\begin{eqnarray} \boldsymbol{J}_{r, \perp } = \sigma _r \frac {\boldsymbol{E} \times \boldsymbol{B}}{B^2} + (\mathcal{P}_{r,\parallel } - \mathcal{P}_{r,\perp }) \frac {\boldsymbol{B}\times \boldsymbol{\kappa }}{B^2} + \frac {1}{B}\left ({\boldsymbol{b}} \times \boldsymbol{\nabla }\mathcal{P}_{r,\perp } \right )\!. \end{eqnarray}
Under the assumption that the plasma consists of thermal particles and REs,
$\boldsymbol{J}=\boldsymbol{J}_i+\boldsymbol{J}_e+\boldsymbol{J}_{r}$
, where i and e correspond to thermal ions and electrons, respectively. By integrating directly over the 3-D velocity vector and coupling the current density into the MHD momentum equation, we have a current coupling scheme:
\begin{eqnarray} \rho \left (\frac {\partial \boldsymbol{u}}{\partial t} + \boldsymbol{u} \boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{u} \right ) = - \sigma _r \boldsymbol{E} + (\boldsymbol{J} - \boldsymbol{J}_r) \times \boldsymbol{B} - \boldsymbol{\nabla }p - \boldsymbol{\nabla }\boldsymbol{\cdot }{\boldsymbol{\varPi }}, \end{eqnarray}
in which the
$\boldsymbol{J}_r$
vector will be easily obtained in the full-kinetic coupled model. In the drift-kinetic coupled model, with
$\boldsymbol{J}_r = \boldsymbol{J}_{r,\parallel }+\boldsymbol{J}_r^{\mathrm {drift}}+\boldsymbol{J}_r^{\mathrm {mag}}$
, we will have a full expression about current density in a drift-kinetic approximation, and the values in three directions will be calculated and coupled into MHD equations.
Inserting the expressions in (2.8) into (2.9), we will have the pressure coupling scheme:
\begin{align} \rho \left (\frac {\partial \boldsymbol{u}}{\partial t} + \boldsymbol{u} \boldsymbol{\cdot }\boldsymbol{\nabla }\boldsymbol{u} \right ) &= - \sigma _r \boldsymbol{E}_\parallel + \boldsymbol{J} \times \boldsymbol{B} - \boldsymbol{\nabla }p - \boldsymbol{\nabla }\boldsymbol{\cdot }{\boldsymbol{\varPi }}\nonumber \\ &\quad - (\mathcal{P}_{r,\parallel }-\mathcal{P}_{r,\perp }){\kappa }-\boldsymbol{\nabla }\mathcal{P}_{r,\perp }. \end{align}
Obviously, in the GC theory, these two schemes are equivalent.
Finally, we will also have Ohm’s law:
\begin{eqnarray} \boldsymbol{E}=-\boldsymbol{u}\times \boldsymbol{B}+\eta (\boldsymbol{J}-\boldsymbol{J}_r). \end{eqnarray}
In this work, an ansatz-based reduced MHD model is employed (Hoelzl et al. Reference Hoelzl2021), which is capable of capturing the key physical details of interest while significantly improving computational efficiency. In JOREK, the terms containing
$\sigma _r$
in the momentum equation due to the low density of the REs are neglected. Additionally, the introduction of the GC model further enhances computational efficiency of the hybrid fluid–kinetic simulations. These advancements enable simulations across long time scales, such as will be needed in the future for instance to capture the full evolution from RE beam formation over secondary deuterium injection towards benign termination.
3. Model verifications
3.1. Tokamak equilibrium with runaway electrons
As part of the validation for the development of the hybrid fluid–kinetic model in this work, we first conduct a benchmark test using an axisymmetric geometry. This provides a preliminary assessment of the performance of the model, ensuring the reliability of the numerical results before applying it to more complex 3-D scenarios.
After a thermal quench, the cold plasma initially tends towards a force-free equilibrium
$(\boldsymbol{J} \times \boldsymbol{B} \approx 0)$
. However, when a substantial fraction of the current is carried by REs, this interpretation is no longer valid (Bandaru & Hoelzl Reference Bandaru and Hoelzl2023), as the contribution of RE pressure becomes significant and cannot be neglected. At high RE energies, a significant Grad–Shafranov major-radial shift arises of the flux surfaces themselves with respect to a force-free equilibrium, which is due to the RE pressure. Furthermore, the RE drift orbits are again shifted with respect to these flux surfaces due to the curvature drift. Moreover, the shift may exceed the radial extent of MHD modes or current layers, potentially altering the linear growth and nonlinear saturation of the instability. The latter will be the target of future work. The effect of the shift on the equilibrium was studied analytically in Bandaru & Hoelzl (Reference Bandaru and Hoelzl2023) which also provided quantitative estimates for the changes in the force balance.
In this section, we benchmark our results against the analytical solutions of Bandaru & Hoelzl (Reference Bandaru and Hoelzl2023) and the full-kinetic coupled model in Bergström et al. (Reference Bergström, Liu, Bandaru and Hoelzl2025). A cold plasma with
$I_p=I_{RE}=50\ \mathrm{kA}$
and an
$R_0=6.2\,\mathrm{m},\ a=2.0\,\mathrm{m}$
circular geometry is assumed. For this ITER-like aspect ratio, the particle orbits are expected to exhibit a pronounced drift from the flux surfaces at energies of tens of MeV. Runaway markers are generated based on a probability function that aligns with the desired current profile. Since the equilibrium solver in JOREK assumes an Ohmic current, an initialisation phase is required where the plasma current transitions from being carried by the thermal electrons to purely by REs. After introducing the runaway current and turning off the Ohmic current source term, the background current will naturally dissipate due to the high resistivity. Since an induced toroidal electric field would otherwise accelerate REs, it is turned off for this verification test in the PiC module to maintain RE energy at a constant value. Eventually, a tokamak equilibrium where the total current is carried by REs is established in this way.
Figure 1(a) illustrates the dependency of the Grad–Shafranov magnetic axis shift on the RE energy, owing to the change in force balance, while figure 1(b) presents the radial dependency of the shift of the flux surfaces and RE drift orbit centres for 50 MeV REs. Both figures compare the results with analytical predictions and with results obtained using the FO kinetic JOREK simulations, which agree very well with the results obtained by our model. For the RE orbit shift calculation, marker electrons with a given energy are traced, and their intersection points with a chosen poloidal cross-section are recorded. The effective orbit surface is reconstructed, and the shift between its centroid and the geometric centre is obtained. After having validated the model in this two-dimensional scenario first, we build further confidence in its ability to capture kinetic effects in more intricate cases, such as 3-D resistive instabilities, as shown in the following subsection.
Figure 1. Comparison with analytical results and full-kinetic treatment. (a) Magnetic axis shift as a function of RE energy; (b) radial shift profiles of 50 MeV REs, with the solid line indicating the flux-surface shift and the dashed line representing the RE orbit shift.
3.2. Three-dimensional linear tearing mode benchmark
In the following, a benchmark for 3-D MHD instabilities and their interaction with REs is provided. While early studies on the interaction between TMs and REs (Helander et al. Reference Helander, Grasso, Hastie and Perona2007) laid the foundation for this topic, numerous theoretical and numerical works have since been conducted (Li et al. Reference Li, Liu, He, Wang, Guo and Zhong2021; Singh et al. Reference Singh, Borgogno, Subba and Grasso2023), in which most of them use a fluid treatment. In the JOREK code, a full-kinetic treatment has already been validated and applied in several beam termination scenarios (Bergström et al. Reference Bergström, Liu, Bandaru and Hoelzl2025). Similarly, to ensure the credibility of the drift-kinetic treatment, we adopt the same safety factor profile and simulation set-up as in the full-kinetic work, and compare the normalised linear results with those from Liu et al. (Reference Liu, Zhao, Jardin, Bhattacharjee, Brennan and Ferraro2020).
In our work, a large aspect ratio is used with
$R_0=10\ \mathrm{m},\ a = 1\ \mathrm{m}$
. Furthermore, a post-disruption plasma with low temperature is assumed, with
$B_0=0.3\,\mathrm{T},\ I_p=I_{RE}=50\ \mathrm{kA},\ \text{and safety factor given by}\ q(r)=1.15(1+r^2/0.6561)$
. To exclude the orbit drift effects and thus make possible a one-to-one comparison with RE fluid simulations, as discussed in § 3.1, the initial marker distribution is set with a kinetic energy of 600 keV and a pitch angle close to unity, yielding a parallel transport at about 90
$\%$
of light speed.
Several key theoretical aspects should be noted, as discussed in the following subsections.
3.2.1. Formation of a narrow sublayer
A narrower sublayer emerges, governed by the ratio of the RE velocity to the Alfvén velocity. The characteristic width is given by (Liu et al. Reference Liu, Zhao, Jardin, Bhattacharjee, Brennan and Ferraro2020)
\begin{eqnarray} \delta =\frac {\gamma v_A}{k_c v_r}, \end{eqnarray}
where
$k_c=n q'/(Rq)$
,
$n$
is the toroidal mode number,
$v_A \approx 6.7\times 10^5\ {\rm m\,s}^{-1}$
is the Alfvén velocity,
$v_r$
is the speed of REs and
$\gamma$
is the growth rate. The RE velocities are typically of the order of the speed of light, yielding a velocity ratio
$v_A/v_r\approx 4 \times 10^{-2}$
. This sublayer remains significantly smaller than the resistive layer which forms in the absence of REs, resulting in a (2,1) RE current structure which is narrower than the corresponding Ohmic current, as shown in figure 2.
Figure 2. The (2,1) normalised current structure radial profiles, in which the blue line corresponds to results for the case with REs and the orange line to those for the case without. The red line is located at the half-maximum.
3.2.2. Impact on linear tearing mode growth rate
The magnetic flux
$\psi$
structure will not be significantly altered by REs; therefore, the standard Furth–Killeen–Rosenbluth growth rate is obtained (Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963). At higher resistivity, however, taking the modification from the local current feature into account (Militello et al. Reference Militello, Huysmans, Ottaviani and Porcelli2004), the growth rate differs between RE-driven and Ohmic plasmas. A general expression for the growth rate is given by (Helander et al. Reference Helander, Grasso, Hastie and Perona2007)
\begin{eqnarray} \frac {(\gamma \eta )^{1/4}}{ k_c^{1/2} }[\gamma -(1-\lambda )\eta b]=\varDelta ^{\prime } \frac {\eta \varGamma \left (1/4\right ) }{2\pi \varGamma \left (3/4\right )}, \end{eqnarray}
where
$b={\psi _0^{(4)}}/{\psi _0^{{\prime }{\prime }}}$
characterises some dominant local high-order current features, accounting for a growth rate reduction in the case of finite resistivity,
$\eta$
is the resistivity and
$\varDelta ^{\prime }$
describes the stability of the TM. It is expressed as
\begin{equation} \varDelta ^\prime = \left ( \frac {1}{\psi } \frac {\text{d}\psi }{\text{d}r} \right )_{r_s^+}^{r_s^-} = \left . \frac {1}{\psi }\frac {\text{d}\psi }{\text{d}r} \right |_{r_s^+} - \left . \frac {1}{\psi }\frac {\text{d}\psi }{\text{d}r} \right |_{r_s^-}, \end{equation}
where
$r_s$
is the minor radius of the rational surface. The superscripts ‘
$+$
’ and ‘
$-$
’ indicate the limits approaching
$r_s$
from the outside and inside, respectively. And in the TM theory, the linear growth rate is decided by (Furth et al. Reference Furth, Rutherford and Selberg1973)
\begin{eqnarray} \gamma =0.5 m^{2/5}\varDelta ^{\prime 4/5}\left(\frac {\eta }{4\pi }\right)^{3/5}\frac {[\text{d}(B_\theta /r)/\text{d}r]^{2/5}}{(4\pi \rho )^{1/5}}, \end{eqnarray}
where
$\rho$
is the plasma density,
$m$
is the poloidal mode number and all quantities are to be evaluated at the rational surface
$r_s$
. Parameter
$\varDelta ^\prime$
is evaluated from the MHD linear simulation results. If
$\lambda = 0$
, the system corresponds to an Ohmic plasma, whereas
$\lambda = 1$
leads to
$J_{total}=J_{RE}$
, recovering the standard Furth–Killeen–Rosenbluth growth rate. This is due to the fact that in the very narrow sublayer, it is challenging to disrupt the constant
$\psi$
condition. But at an extremely high resistivity, constant
$\psi$
will break in a wide sublayer, and the trend with REs will eventually drop.
3.2.3. Frequency excitation by runaway current gradients
In linearised equations, the perturbed RE current
$j_{RE}$
can be rewritten as in the inner layer:
\begin{eqnarray} j_{RE}=\frac {m J_{RE0}^{\prime }}{k_c r_s}\frac {\psi +v_A \phi /c}{x+{\rm i} \gamma v_A/(k_c c)}, \end{eqnarray}
where REs have a light-speed assumption and
$J_{RE0}$
is the equilibrium runaway current density. The coordinate variable x is
$r-r_s$
. But even if REs do not move at the exact speed of light, the conclusion will not be qualitatively altered. Considering a finite value of
$v_A/c$
and keeping the imaginary term in the perturbed runaway current in (3.5), a new
$\gamma$
expression is derived (Liu et al. Reference Liu, Zhao, Jardin, Bhattacharjee, Brennan and Ferraro2020):
\begin{eqnarray} \frac {\gamma ^{5/4}}{\eta ^{3/4} k_c^{1/2} }\frac { 2\pi \varGamma \left (3/4\right )}{\varGamma \left (1/4\right )} = \varDelta ^{\prime } - {\rm i}\pi \frac { m J'_{RE0}}{\left | k_c \right | r_s}. \end{eqnarray}
This expression reveals that a frequency component is excited due to the gradient of the runaway current, a feature absent in Ohmic plasmas. The real and imaginary parts of
$\gamma$
from four different approaches – an eigenvalue code, M3D-C1 fluid simulations, analytical theory and JOREK kinetic simulations – are compared in figure 3 as a function of the normalised resistivity of the background plasma, demonstrating consistency between our JOREK fluid–kinetic model and other methods.
Figure 3. (a) Real and (b) imaginary parts of
$\gamma$
for the (2,1) TM. Red dashed lines represent analytically calculated values. Blue circles indicate results from the eigenvalue code. Orange circles correspond to results from the M3D-C1 simulations. Green circles denote results from the JOREK simulations. The authors gratefully acknowledge C. Liu for providing the data related to the analytical solutions, M3D-C1 and eigenvalue results from Liu et al. (Reference Liu, Zhao, Jardin, Bhattacharjee, Brennan and Ferraro2020).
4. Nonlinear tearing mode dynamics in a runaway beam
4.1. Analytical predictions
As shown in the context of the 3-D verification work of the previous section, there are substantial differences regarding the linear dynamics of TMs between a purely Ohmic plasma and a RE beam. This also reflects in strong differences regarding the nonlinear dynamics as suggested by Hastie, Militello & Porcelli (Reference Hastie, Militello and Porcelli2005) and Helander et al. (Reference Helander, Grasso, Hastie and Perona2007). Due to the fact that the velocity of REs following the magnetic field lines is at the speed of light, the response of the RE current to magnetic field perturbations differs from that of the Ohmic current, leading to different saturation states. In the RE-driven case, the runaway current remains ‘frozen into’ the magnetic field throughout island evolution, whereas in the resistive case, the Ohmic current is governed by the flux-surface average of Ohm’s law, leading to different saturated states. In a slab geometry, the expressions predicting the saturated island widths are given in Helander et al. (Reference Helander, Grasso, Hastie and Perona2007):
\begin{eqnarray} w_{RE}=-\frac {j_0(0)}{j_0^{{\prime }{\prime }}(0)}\frac {\varDelta ^{\prime }}{0.272}\quad \text{and}\quad w_{MHD}=-\frac {j_0(0)}{j_0^{{\prime }{\prime }}(0)}\frac {\varDelta ^{\prime }}{0.411}. \end{eqnarray}
The predictions are made under the condition that the island is small, i.e.
$w, \varDelta ^{\prime }\ll 1$
, and in the presence of REs is approximately 1.5 times larger than in the Ohmic case under these assumptions.
4.2. Simulation results
In our work, we consider two cases with different equilibria in which the TM has different values of
$\varDelta ^\prime $
. Poincaré plots of the saturated islands with and without REs are shown in figures 4 and 5. The former corresponds to
$\varDelta ^\prime \approx 0.2$
and the latter to
$\varDelta ^\prime \approx 2.0$
. In figure 4, the width ratio is approximately 1.7, close to the analytically predicted value, while for the more unstable case with
$\varDelta ^\prime \approx 2.0$
, the ratio is larger than 2. In the latter case, larger islands emerge, leading to enhanced mode coupling and a more complex magnetic topology with initial signs of magnetic field stochastisation around the island separatrix. In such cases, the evolution becomes complex and more difficult to predict analytically.
Figure 4. Poincaré plots of saturated islands formed (a) in the presence of REs and (b) without REs, for the case with
${\varDelta }^{\prime }\approx 0.2$
.
Figure 5. Poincaré plots of saturated islands formed (a) in the presence of REs and (b) without REs, for the case with
${\varDelta }^{\prime }\approx 2.0$
.
Figure 6 shows the evolution of the (2,1) current half-widths with and without REs, which is defined as in figure 2. As discussed in § 3.2, the presence of a sublayer causes the structure with REs to be much narrower than the Ohmic case in the linear stage. However, in the nonlinear phase, the width with REs expands compared with the Ohmic current. Due to the rapid response of relativistic REs to perturbations, the TM instability quickly enters into the nonlinear stage.
Figure 6. The (2,1) current width evolution with time for the cases (a) with REs and (b) without REs (full width at half maximum). While the current layer in the linear phase is more narrow in the presence of REs compared with the Ohmic scenario, it becomes much wider in the nonlinear phase.
In figure 7, the magnetic and kinetic energy evolution of the n = 0 and n = 1 toroidal harmonics with time is depicted. Also shown are the logarithmic values of the saturated normalised energies. As predicted, the
$n=1$
magnetic energy with REs is much larger than that of the Ohmic plasma; however, the
$n=1$
kinetic energy in a RE-driven TM is smaller. The reason is that the Lorenz force will not play the same role in a RE-driven TM. If starting from a classical slab TM as in figure 8, it is known that if there is a perturbation magnetic field, an out-of-plane electric field
$\boldsymbol{E}_1$
can be induced according to Faraday’s law. Based on Ohm’s law, a current
$\boldsymbol{J}_1$
is generated, and also a flow
$\boldsymbol{u}_1$
is induced. The Lorentz force caused by the toroidal current and the poloidal magnetic field pushes outward at the O-point and squeezes inward at the X-point, causing further changes in the topology. This induces a new electric field, creating a positive feedback loop that promotes the growth of the magnetic island. However, in a RE-driven plasma, this positive feedback mechanism differs. Given that RE toroidal transit time is several orders shorter than the Alfvén time, the (2,1) RE current directly responds to perturbations. The magnetic flux within the island increases, enhancing the perturbed magnetic field and consequently affecting the trajectories of the REs. The increase of perturbed
$\psi$
within the island intensifies the magnetic reconnection process, which leads to a stronger perturbation magnetic field and a widening of the magnetic island. This process describes how the islands are driven by REs. The momentum perturbation of the bulk plasma is decoupled with the evolution of magnetic fields, so the kinetic energy will not increase much, even if the magnetic reconnection strengthens. In figure 9, the velocity fields are presented, separately with REs and without REs, in which the colourbar is from the absolute value of the velocity, and the arrows point in the direction of reconnection flows. It is clear that the reconnection flows are much weaker if driven by REs. From the fluid momentum equation, it can be seen that the Lorentz force no longer accelerates the fluid. The disappearance of this term results in the decoupling, which accounts for the evolution of both magnetic and kinetic energy.
Figure 7. Time evolution of the magnetic and kinetic energies in the n = 0 and n = 1 toroidal harmonics for the cases (a) with REs and (b) without REs.
Figure 8. An example of magnetic field line reconnection in a slab geometry. See the main text for a detailed explanation.
Figure 9. Reconnection flow: velocity field and vector arrows around the X-point of islands in the
$\phi =0$
R–Z plane (a) with REs and (b) without REs.
5. Conclusion
In this work, we have developed and validated a hybrid fluid–kinetic model within the JOREK framework to investigate the interaction between REs and large-scale MHD instabilities. By exploiting a drift-kinetic approach for the full-f PiC model used to describe the REs, the model is able to efficiently calculate the co-evolution of slowly growing MHD instabilities in self-consistent interaction with the relativistic kinetic RE dynamics. By benchmarking our model against analytical theory and existing numerical results, we have demonstrated its capability to capture the essential physics of the effect of REs on MHD instabilities. This includes a two-dimensional verification regarding the major-radial force balance and RE drift orbits, as well as a verification of the linear TM growth rates in the presence of a RE beam. Here, REs introduce a narrow sublayer, modifying the resistive layer and growth rates. The RE current gradients introduce a frequency component, a feature absent in Ohmic plasmas.
In the main studies of this work, we investigated nonlinear TM dynamics in a RE beam. In the nonlinear regime, REs significantly impact the evolution and saturation of magnetic islands. We observe that the presence of REs increases the saturated island width compared with the classical Ohmic case, consistent with theoretical predictions. The predictions no longer hold at high values of
$\varDelta ^{\prime }$
, and kinetic REs will drive larger islands and more complex magnetic topology. Furthermore, energy analysis shows that while the magnetic energy of the (2,1) mode grows substantially in the presence of REs, the kinetic energy remains lower than in the Ohmic case due to the decoupling of fluid and magnetic fields. Unlike classical TMs, where the Lorentz force plays a central role in accelerating fluid motion, in RE-driven modes, the perturbed RE current within the island enhances the magnetic reconnection process, leading to island growth without significantly accelerating the bulk plasma.
These findings provide insights into the role of REs in modifying MHD instabilities, which is crucial for understanding disruption dynamics in tokamaks, e.g. in view of exploiting the MHD dynamics for benign RE beam termination. Building upon the results of this study, our next steps will focus on further exploring the RE curvature drift effect (in § 3.1) on TM instabilities. In particular, we will analyse how variations in RE energy affect the linear TM characteristics, where further differences are expected between mono-energetic RE beams and those with a broad energy distribution. Depending on the parameters, the shift between flux surfaces and RE orbits can exceed the resistive layer width of classical TM instabilities, modifying their stability properties. Simultaneously, there are ongoing efforts to model the problem analytically, which focuses on cases where the shift is either much smaller or significantly larger than the resistive layer width. By combining numerical simulations with analytical approaches, we intend to refine our understanding of how kinetic corrections influence TM growth and stability in the presence of REs. These investigations will further extend the applicability of our hybrid fluid–kinetic model, providing a more comprehensive framework for studying RE dynamics in tokamaks, e.g. RE mitigation, which is of particular relevance for finding pathways to benign termination.
Acknowledgements
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Funding
Part of this work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200 – EUROfusion). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. Some of the simulations were done on the Marconi-Fusion supercomputer hosted at CINECA. The authors gratefully acknowledge MPCDF (https://www.mpcdf.mpg.de) for providing computing time on the Supercomputer VIPER. Open access funding provided by Max Planck Society.
Declaration of interests
The authors report no conflict of interest.
Open access
