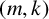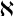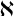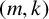1 Introduction
If G is a group, H is a subgroup of G and
![]() $(m,k)$
is a pair of nonnegative integers, following [Reference Dixon, Ferrara and Trombetti7], H is said to be
$(m,k)$
is a pair of nonnegative integers, following [Reference Dixon, Ferrara and Trombetti7], H is said to be
![]() $(m,k)$
-subnormal in G if there is a subgroup
$(m,k)$
-subnormal in G if there is a subgroup
![]() $H_0$
containing H such that
$H_0$
containing H such that
![]() $\vert H_0:H \vert \leq m$
and
$\vert H_0:H \vert \leq m$
and
![]() $H_0$
is subnormal in G with defect at most k. The pairs
$H_0$
is subnormal in G with defect at most k. The pairs
![]() $(m,k)$
are ordered lexicographically; with this ordering, if H is
$(m,k)$
are ordered lexicographically; with this ordering, if H is
![]() $(m,k)$
-subnormal for some pair
$(m,k)$
-subnormal for some pair
![]() $(m,k)$
, then the least such pair is called the near defect of H in G (see [Reference Lennox9]). Lennox [Reference Lennox9, Reference Lennox10] called a subgroup almost subnormal if it is
$(m,k)$
, then the least such pair is called the near defect of H in G (see [Reference Lennox9]). Lennox [Reference Lennox9, Reference Lennox10] called a subgroup almost subnormal if it is
![]() $(m,k)$
-subnormal for certain nonnegative integers
$(m,k)$
-subnormal for certain nonnegative integers
![]() $m,k$
. Clearly, a subgroup H is
$m,k$
. Clearly, a subgroup H is
![]() $(m,1)$
-subnormal in G if and only if it has index at most m in its normal closure
$(m,1)$
-subnormal in G if and only if it has index at most m in its normal closure
![]() $H^G$
, while H is
$H^G$
, while H is
![]() $(1,k)$
-subnormal if and only if it is subnormal of defect at most k.
$(1,k)$
-subnormal if and only if it is subnormal of defect at most k.
It follows from theorems of Neumann [Reference Neumann12] and Macdonald [Reference Macdonald11] that if a group admits only
![]() $(m,1)$
-subnormal subgroups for a fixed positive integer m, then its commutator subgroup is finite of order bounded by a function of m. On the other hand, a well-known theorem of Roseblade [Reference Roseblade16] asserts that there exists a function f such that if G is a group in which every subgroup is
$(m,1)$
-subnormal subgroups for a fixed positive integer m, then its commutator subgroup is finite of order bounded by a function of m. On the other hand, a well-known theorem of Roseblade [Reference Roseblade16] asserts that there exists a function f such that if G is a group in which every subgroup is
![]() $(1,k)$
-subnormal for a fixed positive integer k, then G is nilpotent of class bounded by
$(1,k)$
-subnormal for a fixed positive integer k, then G is nilpotent of class bounded by
![]() $f(k)$
.
$f(k)$
.
Lennox [Reference Lennox9] generalised Roseblade’s theorem, proving that there exists a function
![]() $\mu $
such that if every finitely generated subgroup of a group G is
$\mu $
such that if every finitely generated subgroup of a group G is
![]() $(m,k)$
-subnormal in G, then the term
$(m,k)$
-subnormal in G, then the term
![]() $\gamma _{\mu (m+k)}(G)$
of the lower central series of G is finite of order less than or equal to
$\gamma _{\mu (m+k)}(G)$
of the lower central series of G is finite of order less than or equal to
![]() $m!$
.
$m!$
.
A group G is said to have finite rank if there is a positive integer r such that every finitely generated subgroup of G can be generated by at most r elements; if such an r does not exist, we say that the group G has infinite rank. In a long series of papers, it has been shown that the structure of a (soluble) group of infinite rank is strongly influenced by that of its proper subgroups of infinite rank; in particular, Evans and Kim [Reference Evans and Kim8] studied locally soluble groups of infinite rank in which all subgroups of infinite rank are subnormal with bounded defect, while in [Reference Dixon, Ferrara and Trombetti7] locally soluble groups of infinite rank whose subgroups of infinite rank are
![]() $(m,k)$
-subnormal were considered. The results obtained in that context suggest that the behaviour of small subgroups in a large group can be neglected, at least for the right choice of the definition of largeness (and within a suitable universe); for instance, in [Reference De Falco, de Giovanni, Heineken and Musella3] the authors consider uncountable groups, of cardinality
$(m,k)$
-subnormal were considered. The results obtained in that context suggest that the behaviour of small subgroups in a large group can be neglected, at least for the right choice of the definition of largeness (and within a suitable universe); for instance, in [Reference De Falco, de Giovanni, Heineken and Musella3] the authors consider uncountable groups, of cardinality
![]() $\aleph $
say, in which all subgroups of cardinality
$\aleph $
say, in which all subgroups of cardinality
![]() $\aleph $
are normal or subnormal. In a series of subsequent papers (see [Reference De Falco, Evans, de Giovanni and Musella4–Reference De Falco, de Giovanni and Musella6]), similar problems were considered, by replacing normality with some of its relevant generalisations. The main obstacle in the study of groups of large cardinality
$\aleph $
are normal or subnormal. In a series of subsequent papers (see [Reference De Falco, Evans, de Giovanni and Musella4–Reference De Falco, de Giovanni and Musella6]), similar problems were considered, by replacing normality with some of its relevant generalisations. The main obstacle in the study of groups of large cardinality
![]() $\aleph $
is the existence of infinite groups in which all proper subgroups have cardinality strictly smaller than
$\aleph $
is the existence of infinite groups in which all proper subgroups have cardinality strictly smaller than
![]() $\aleph $
(the so-called Jónsson groups). Clearly, a countably infinite group is a Jónsson group if and only if all its proper subgroups are finite, so that Prüfer groups and Tarski groups (that is, infinite simple groups whose proper nontrivial subgroups have prime order) have the Jónsson property. On the other hand, it is known that if G is an uncountable Jónsson group, then
$\aleph $
(the so-called Jónsson groups). Clearly, a countably infinite group is a Jónsson group if and only if all its proper subgroups are finite, so that Prüfer groups and Tarski groups (that is, infinite simple groups whose proper nontrivial subgroups have prime order) have the Jónsson property. On the other hand, it is known that if G is an uncountable Jónsson group, then
![]() $G/Z(G)$
is simple and
$G/Z(G)$
is simple and
![]() $G' = G$
(see, for instance, [Reference De Falco, de Giovanni, Heineken and Musella3, Corollary 2.6]). Relevant examples of Jónsson groups of cardinality
$G' = G$
(see, for instance, [Reference De Falco, de Giovanni, Heineken and Musella3, Corollary 2.6]). Relevant examples of Jónsson groups of cardinality
![]() $\aleph _1$
have been constructed by Shelah [Reference Shelah17] and Obraztsov [Reference Obraztsov13].
$\aleph _1$
have been constructed by Shelah [Reference Shelah17] and Obraztsov [Reference Obraztsov13].
If G is an uncountable group, a subgroup H of G will be called large if it has the same cardinality as G and small otherwise. The aim of the paper is to make a further contribution to the study of the influence of the behaviour of large subgroups on the structure of a group, by considering uncountable groups whose large subgroups are
![]() $(m,k)$
-subnormal for a fixed pair
$(m,k)$
-subnormal for a fixed pair
![]() $(m,k)$
.
$(m,k)$
.
Most of our notation is standard and can be found in [Reference Robinson15].
2 Statements and proofs
Throughout this paper,
![]() $\aleph $
will denote a fixed uncountable regular cardinal number and, for nonnegative integers
$\aleph $
will denote a fixed uncountable regular cardinal number and, for nonnegative integers
![]() $(m,k)$
, we define the group class
$(m,k)$
, we define the group class
![]() $\mathfrak {X}(m,k)$
to be the class of all groups of cardinality
$\mathfrak {X}(m,k)$
to be the class of all groups of cardinality
![]() $\aleph $
(and the trivial groups) whose large subgroups are
$\aleph $
(and the trivial groups) whose large subgroups are
![]() $(m,k)$
-subnormal in G. We begin this section by showing that the Baer radical of an
$(m,k)$
-subnormal in G. We begin this section by showing that the Baer radical of an
![]() $\mathfrak {X}(m,k)$
-group has all large subgroups subnormal with bounded defect.
$\mathfrak {X}(m,k)$
-group has all large subgroups subnormal with bounded defect.
Lemma 2.1. Let G be a locally nilpotent group. Then every
![]() $(m,k)$
-subnormal subgroup of G is subnormal in G of defect at most
$(m,k)$
-subnormal subgroup of G is subnormal in G of defect at most
![]() $m+k$
.
$m+k$
.
Proof. Let H be an
![]() $(m,k)$
-subnormal subgroup of G, so that there exists a subnormal subgroup X of G of defect at most k such that
$(m,k)$
-subnormal subgroup of G, so that there exists a subnormal subgroup X of G of defect at most k such that
![]() $\lvert X:H\rvert \leq m$
. If
$\lvert X:H\rvert \leq m$
. If
![]() $N=H_{X}$
is the normal core of H in X, then
$N=H_{X}$
is the normal core of H in X, then
![]() $X/N$
is a finite nilpotent group, so
$X/N$
is a finite nilpotent group, so
![]() $H/N$
is subnormal in
$H/N$
is subnormal in
![]() $X/N$
with defect at most m. Hence, H is a subnormal subgroup of G of defect at most
$X/N$
with defect at most m. Hence, H is a subnormal subgroup of G of defect at most
![]() $m+k$
.
$m+k$
.
Corollary 2.2. Let G be a locally nilpotent
![]() $\mathfrak {X}(m,k)$
-group. If G contains a large abelian subgroup, then G is nilpotent of class at most
$\mathfrak {X}(m,k)$
-group. If G contains a large abelian subgroup, then G is nilpotent of class at most
![]() $f(m+k)$
.
$f(m+k)$
.
Proof. The assertion is a consequence of Lemma 2.1 and [Reference De Falco, de Giovanni, Heineken and Musella3, Theorem 2.5].
Corollary 2.3. Let G be an
![]() $\mathfrak {X}(m,k)$
-group containing a large abelian subgroup. Then the Baer radical of G is large and nilpotent of class at most
$\mathfrak {X}(m,k)$
-group containing a large abelian subgroup. Then the Baer radical of G is large and nilpotent of class at most
![]() $f(m+k)$
.
$f(m+k)$
.
Proof. Let A be a large abelian subgroup; then A is
![]() $(m,k)$
-subnormal in G, so that there exists a subnormal subgroup C of defect at most k such that
$(m,k)$
-subnormal in G, so that there exists a subnormal subgroup C of defect at most k such that
![]() $\lvert C:A\rvert \leq m$
. It follows that
$\lvert C:A\rvert \leq m$
. It follows that
![]() $A_{C}$
, the normal core of A in C, is a large abelian subnormal subgroup of G. Thus, B is a locally nilpotent
$A_{C}$
, the normal core of A in C, is a large abelian subnormal subgroup of G. Thus, B is a locally nilpotent
![]() $\mathfrak {X}(m,k)$
-group containing a large abelian subgroup. The statement is now a consequence of Corollary 2.2.
$\mathfrak {X}(m,k)$
-group containing a large abelian subgroup. The statement is now a consequence of Corollary 2.2.
Proposition 2.4. Let G be a group of cardinality
![]() $\aleph $
. If there exists a positive integer r such that
$\aleph $
. If there exists a positive integer r such that
![]() $\gamma _{r}(G)$
is small, then for every finitely generated subgroup F of G, the centraliser
$\gamma _{r}(G)$
is small, then for every finitely generated subgroup F of G, the centraliser
![]() $C_G(F)$
is a large subgroup of G.
$C_G(F)$
is a large subgroup of G.
Proof. Let s be the least positive integer such that
![]() $\gamma _{s+1}(G)$
is small and let g be any element of G; if we put
$\gamma _{s+1}(G)$
is small and let g be any element of G; if we put
the function
is a bijection and, therefore, the set
![]() $g^{\gamma _{s}(G)}$
has cardinality strictly smaller than
$g^{\gamma _{s}(G)}$
has cardinality strictly smaller than
![]() $\aleph $
. However,
$\aleph $
. However,
where
![]() $C_{\gamma _{s}(G)}(g)$
is the centraliser in
$C_{\gamma _{s}(G)}(g)$
is the centraliser in
![]() $\gamma _{s}(G)$
of g.
$\gamma _{s}(G)$
of g.
Put
![]() $F=\langle g_{1}, \ldots , g_{t}\rangle $
; then
$F=\langle g_{1}, \ldots , g_{t}\rangle $
; then
![]() $\lvert \gamma _{s}(G):C_{\gamma _{s}(G)}(g_i)\rvert $
is strictly smaller than
$\lvert \gamma _{s}(G):C_{\gamma _{s}(G)}(g_i)\rvert $
is strictly smaller than
![]() $\aleph $
, for each
$\aleph $
, for each
![]() $i \in \{1,\ldots ,t\}$
. Moreover,
$i \in \{1,\ldots ,t\}$
. Moreover,
 $$ \begin{align*} C_{G}(F)=\overset{t}{\underset{i=1}{\bigcap}}C_{G}(g_{i}), \end{align*} $$
$$ \begin{align*} C_{G}(F)=\overset{t}{\underset{i=1}{\bigcap}}C_{G}(g_{i}), \end{align*} $$
so that
![]() $\lvert \gamma _{s}(G):C_{\gamma _{s}(G)}(F)\rvert $
is strictly smaller than
$\lvert \gamma _{s}(G):C_{\gamma _{s}(G)}(F)\rvert $
is strictly smaller than
![]() $\aleph $
, and hence
$\aleph $
, and hence
![]() $C_G(F)$
is a large subgroup of G.
$C_G(F)$
is a large subgroup of G.
Phillips [Reference Phillips14] introduced the following generalisation of subnormality for infinite groups: a subgroup H of a group G is called f-subnormal in G if there exists an f-series from H to G, that is, a finite series
such that either
![]() $H_i$
is normal in
$H_i$
is normal in
![]() $H_{i+1}$
or
$H_{i+1}$
or
![]() $\vert H_{i+1}{\,:\,}H_i \vert <\infty $
for every
$\vert H_{i+1}{\,:\,}H_i \vert <\infty $
for every
![]() $i\in \{ 0, \ldots ,n-1 \}$
.
$i\in \{ 0, \ldots ,n-1 \}$
.
Clearly, every
![]() $(m,k)$
-subnormal subgroup is f-subnormal.
$(m,k)$
-subnormal subgroup is f-subnormal.
Corollary 2.5. Let G be an
![]() $\mathfrak {X}(m,k)$
-group. If there exists a positive integer r such that
$\mathfrak {X}(m,k)$
-group. If there exists a positive integer r such that
![]() $\gamma _{r}(G)$
is small, then every finitely generated subgroup F of G is f-subnormal in G.
$\gamma _{r}(G)$
is small, then every finitely generated subgroup F of G is f-subnormal in G.
Proof. It follows from Proposition 2.4 that
![]() $C_{G}(F)F$
is an
$C_{G}(F)F$
is an
![]() $(m,k)$
-subnormal subgroup of G in which F is normal.
$(m,k)$
-subnormal subgroup of G in which F is normal.
Lemma 2.6. Let G be an
![]() $\mathfrak {X}(m,k)$
-group. If G is abelian-by-cyclic, then it is finite-by-nilpotent and
$\mathfrak {X}(m,k)$
-group. If G is abelian-by-cyclic, then it is finite-by-nilpotent and
![]() $\lvert \gamma _{\mu (m+k)}(G)\rvert \leq (m{!})^{2}$
.
$\lvert \gamma _{\mu (m+k)}(G)\rvert \leq (m{!})^{2}$
.
Proof. We can write
![]() $G=A\langle x\rangle $
, where A is a normal abelian subgroup of G and x is an element of G. Of course, A is large and it can be regarded as a module over the countable ring
$G=A\langle x\rangle $
, where A is a normal abelian subgroup of G and x is an element of G. Of course, A is large and it can be regarded as a module over the countable ring
![]() $R=\mathbb {Z}\langle x\rangle $
. Moreover, the R-submodules of A are all its G-invariant subgroups. By [Reference De Falco, de Giovanni, Heineken and Musella3, Lemma 2.3], A contains the direct product
$R=\mathbb {Z}\langle x\rangle $
. Moreover, the R-submodules of A are all its G-invariant subgroups. By [Reference De Falco, de Giovanni, Heineken and Musella3, Lemma 2.3], A contains the direct product
where I is a set of cardinality
![]() $\aleph $
and, for each
$\aleph $
and, for each
![]() $i \in I$
,
$i \in I$
,
![]() $M_{i}$
is a G-invariant subgroup of A. It follows that there exist two subsets
$M_{i}$
is a G-invariant subgroup of A. It follows that there exist two subsets
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
of I, each of cardinality
$I_{2}$
of I, each of cardinality
![]() $\aleph $
, such that
$\aleph $
, such that
For
![]() $j=1,2$
, put
$j=1,2$
, put
then
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
are G-invariant subgroups of A of cardinality
$B_{2}$
are G-invariant subgroups of A of cardinality
![]() $\aleph $
whose intersection is trivial. Thus, [Reference Lennox9, Theorem A] ensures that, for
$\aleph $
whose intersection is trivial. Thus, [Reference Lennox9, Theorem A] ensures that, for
![]() $j=1,2$
,
$j=1,2$
,
Therefore,
![]() $\lvert \gamma _{\mu (m+k)}(G)\rvert \leq (m{!})^{2}$
and G is finite-by-nilpotent.
$\lvert \gamma _{\mu (m+k)}(G)\rvert \leq (m{!})^{2}$
and G is finite-by-nilpotent.
Lemma 2.7. Let G be an
![]() $\mathfrak {X}(m,k)$
-group containing a large abelian normal subgroup. Then G is locally finite-by-nilpotent, and if B is the Baer radical of G, then
$\mathfrak {X}(m,k)$
-group containing a large abelian normal subgroup. Then G is locally finite-by-nilpotent, and if B is the Baer radical of G, then
![]() $G/B$
has finite exponent.
$G/B$
has finite exponent.
Proof. Let x be any element of G and let A be a large abelian normal subgroup of G; the subgroup
![]() $\langle A, x \rangle = A\langle x\rangle $
is an abelian-by-cyclic
$\langle A, x \rangle = A\langle x\rangle $
is an abelian-by-cyclic
![]() $\mathfrak {X}(m,k)$
-group so, by Lemma 2.6,
$\mathfrak {X}(m,k)$
-group so, by Lemma 2.6,
![]() $\lvert \gamma _{\mu (m+k)}(A\langle x\rangle )\rvert \leq (m{!})^2$
. Therefore,
$\lvert \gamma _{\mu (m+k)}(A\langle x\rangle )\rvert \leq (m{!})^2$
. Therefore,
![]() $\langle x \rangle $
has index at most
$\langle x \rangle $
has index at most
![]() $(m{!})^2$
in
$(m{!})^2$
in
![]() $\langle x\rangle \gamma _{\mu (m+k)}(A\langle x\rangle )$
. Since
$\langle x\rangle \gamma _{\mu (m+k)}(A\langle x\rangle )$
. Since
![]() $A\langle x\rangle /\gamma _{\mu (m+k)}(A\langle x\rangle )$
is nilpotent of class at most
$A\langle x\rangle /\gamma _{\mu (m+k)}(A\langle x\rangle )$
is nilpotent of class at most
![]() $\mu (m+k)-1$
, the subgroup
$\mu (m+k)-1$
, the subgroup
![]() $\langle x\rangle \gamma _{\mu (m+k)}(A\langle x\rangle )$
is subnormal in
$\langle x\rangle \gamma _{\mu (m+k)}(A\langle x\rangle )$
is subnormal in
![]() $A\langle x\rangle $
with defect at most
$A\langle x\rangle $
with defect at most
![]() $\mu (m+k)-1$
. Finally,
$\mu (m+k)-1$
. Finally,
![]() $A\langle x\rangle $
is
$A\langle x\rangle $
is
![]() $(m,k)$
-subnormal in G and so it has index at most m in
$(m,k)$
-subnormal in G and so it has index at most m in
![]() $(A\langle x\rangle )^{G,k}$
which is subnormal in G with defect at most k.
$(A\langle x\rangle )^{G,k}$
which is subnormal in G with defect at most k.
By an application of [Reference Lennox9, Theorem B], G is locally finite-by-nilpotent.
Let X be a cyclic subgroup of G. By the above argument, there exists a chain
such that either
![]() $X_{i+1}$
is subnormal in
$X_{i+1}$
is subnormal in
![]() $X_i$
with defect at most
$X_i$
with defect at most
![]() $\mu (m+k)-1$
or
$\mu (m+k)-1$
or
![]() $X_{i+1}$
has index at most
$X_{i+1}$
has index at most
![]() $(m{!})^2$
in
$(m{!})^2$
in
![]() $X_i$
; we shall prove by induction on the length of the chain that for every cyclic subgroup X of G, there is a positive integer s dividing
$X_i$
; we shall prove by induction on the length of the chain that for every cyclic subgroup X of G, there is a positive integer s dividing
![]() $\beta (m)=((m{!})^2)!$
such that
$\beta (m)=((m{!})^2)!$
such that
![]() $X^{s}$
is subnormal in G.
$X^{s}$
is subnormal in G.
We can assume that
![]() $X^{s}$
is subnormal in
$X^{s}$
is subnormal in
![]() $X_1$
, for some positive integer s dividing
$X_1$
, for some positive integer s dividing
![]() $\beta (m)$
. If
$\beta (m)$
. If
![]() $X_1$
is subnormal in G, then
$X_1$
is subnormal in G, then
![]() $X^{s}$
is subnormal in G. So we can assume that the index
$X^{s}$
is subnormal in G. So we can assume that the index
![]() $\vert G:X_1 \vert \leq (m{!})^2$
; then the core Y of
$\vert G:X_1 \vert \leq (m{!})^2$
; then the core Y of
![]() $X_1$
in G has index at most
$X_1$
in G has index at most
![]() $((m{!})^2)!= \beta (m)$
in G. Hence,
$((m{!})^2)!= \beta (m)$
in G. Hence,
![]() $X^{\beta (m)}$
is a normal subgroup of
$X^{\beta (m)}$
is a normal subgroup of
![]() $Y\cap X^{s}$
, which is subnormal in Y. It follows that
$Y\cap X^{s}$
, which is subnormal in Y. It follows that
![]() $X^{\beta (m)}$
is subnormal in G, and hence
$X^{\beta (m)}$
is subnormal in G, and hence
![]() $X^{\beta (m)} \leq B$
.
$X^{\beta (m)} \leq B$
.
Therefore,
![]() $G/B$
has finite exponent.
$G/B$
has finite exponent.
The following result depends on [Reference Burns, Okoh, Smith and Wiegold1, Theorem 1
![]() ${}^{\prime }$
]. Recalling that an abelian normal subgroup A of a group G can be regarded as a module over the group ring
${}^{\prime }$
]. Recalling that an abelian normal subgroup A of a group G can be regarded as a module over the group ring
![]() $\mathbb {Z}(G/C_{G}(A))$
, we obtain the following interesting lemma.
$\mathbb {Z}(G/C_{G}(A))$
, we obtain the following interesting lemma.
Lemma 2.8. Let G be a group containing an uncountable abelian normal subgroup A. If
![]() $G/C_{G}(A)$
is finite, then A contains a subgroup of the form
$G/C_{G}(A)$
is finite, then A contains a subgroup of the form
where the set I has the same cardinality as A.
Lemma 2.9. Let G be an
![]() $\mathfrak {X}(m,k)$
-group. If G contains a large nilpotent normal subgroup N such that
$\mathfrak {X}(m,k)$
-group. If G contains a large nilpotent normal subgroup N such that
![]() $G/N$
is locally finite, then
$G/N$
is locally finite, then
![]() $\gamma _{\mu (m^{2}+k)}(G)$
is small.
$\gamma _{\mu (m^{2}+k)}(G)$
is small.
Proof. Since N is nilpotent of cardinality
![]() $\aleph $
, there exists a nonnegative integer r such that
$\aleph $
, there exists a nonnegative integer r such that
![]() $\lvert Z_{r}(N)\rvert < \aleph $
and
$\lvert Z_{r}(N)\rvert < \aleph $
and
![]() $\lvert Z_{r+1}(N)\rvert =\aleph $
. So, the section
$\lvert Z_{r+1}(N)\rvert =\aleph $
. So, the section
![]() $\overline {A}=Z_{r+1}(N)/Z_{r}(N)$
is an abelian normal subgroup of
$\overline {A}=Z_{r+1}(N)/Z_{r}(N)$
is an abelian normal subgroup of
![]() $\overline {G}=G/Z_{r}(N)$
. Let
$\overline {G}=G/Z_{r}(N)$
. Let
![]() $\overline {E}$
be any finitely generated subgroup of
$\overline {E}$
be any finitely generated subgroup of
![]() $\overline {G}$
and put
$\overline {G}$
and put
![]() $\overline {L}=\overline {E}\overline {A}$
. Since
$\overline {L}=\overline {E}\overline {A}$
. Since
![]() $\overline {N}\cap \overline {L} \leq C_{\overline {L}}(\overline {A})$
, then
$\overline {N}\cap \overline {L} \leq C_{\overline {L}}(\overline {A})$
, then
![]() $\overline {L}/C_{\overline {L}}(\overline {A})$
is finite, so that Lemma 2.8 ensures that
$\overline {L}/C_{\overline {L}}(\overline {A})$
is finite, so that Lemma 2.8 ensures that
![]() $\overline {A}$
contains a subgroup
$\overline {A}$
contains a subgroup
![]() $\overline {H}$
of the form
$\overline {H}$
of the form
where I is a set of cardinality
![]() $\aleph $
and, for each
$\aleph $
and, for each
![]() $i \in I$
,
$i \in I$
,
![]() $\overline {A}_{i}$
is a nontrivial normal subgroup of
$\overline {A}_{i}$
is a nontrivial normal subgroup of
![]() $\overline {L}$
. So we can find two
$\overline {L}$
. So we can find two
![]() $\overline {L}$
-invariant subgroups
$\overline {L}$
-invariant subgroups
![]() $\overline {H}_{1}$
and
$\overline {H}_{1}$
and
![]() $\overline {H}_{2}$
of
$\overline {H}_{2}$
of
![]() $\overline {H}$
, both of cardinality
$\overline {H}$
, both of cardinality
![]() $\aleph $
and such that
$\aleph $
and such that
Therefore,
is the intersection of two
![]() $(m,k)$
-subnormal subgroups of
$(m,k)$
-subnormal subgroups of
![]() $\overline {G}$
and, by [Reference Dixon, Ferrara and Trombetti7, Lemma 2.5],
$\overline {G}$
and, by [Reference Dixon, Ferrara and Trombetti7, Lemma 2.5],
![]() $\overline {E}$
is
$\overline {E}$
is
![]() $(m^{2},k)$
-subnormal. An application of [Reference Lennox9, Theorem A] completes the proof.
$(m^{2},k)$
-subnormal. An application of [Reference Lennox9, Theorem A] completes the proof.
We are now able to state and prove our first main theorem.
Theorem 2.10. Let G be an
![]() $\mathfrak {X}(m,k)$
-group. If G contains a large abelian normal subgroup, then G is finite-by-nilpotent and
$\mathfrak {X}(m,k)$
-group. If G contains a large abelian normal subgroup, then G is finite-by-nilpotent and
![]() $\lvert \gamma _{\mu (m^2+k)}(G)\rvert \leq (m^{2})!$
.
$\lvert \gamma _{\mu (m^2+k)}(G)\rvert \leq (m^{2})!$
.
Proof. Let B be the Baer radical of G; it follows from Corollary 2.3 and Lemma 2.7 that B is nilpotent and
![]() $G/B$
is a locally finite group, so that
$G/B$
is a locally finite group, so that
![]() $\gamma _{\mu (m+k)}(G)$
is small by Lemma 2.9. Let F be any finitely generated subgroup of G. Applying Proposition 2.4 to the group
$\gamma _{\mu (m+k)}(G)$
is small by Lemma 2.9. Let F be any finitely generated subgroup of G. Applying Proposition 2.4 to the group
![]() $AF$
, we can say that
$AF$
, we can say that
![]() $C_{AF}(F)$
is large, so that also
$C_{AF}(F)$
is large, so that also
![]() $C_{AF}(F) \cap A$
is a large subgroup. It follows that
$C_{AF}(F) \cap A$
is a large subgroup. It follows that
![]() $Z(AF)$
is large, and hence it contains two large subgroups
$Z(AF)$
is large, and hence it contains two large subgroups
![]() $U_{1}$
and
$U_{1}$
and
![]() $U_{2}$
such that
$U_{2}$
such that
Therefore,
is the intersection of two
![]() $(m,k)$
-subnormal subgroups of G and, by [Reference Dixon, Ferrara and Trombetti7, Lemma 2.5], F is
$(m,k)$
-subnormal subgroups of G and, by [Reference Dixon, Ferrara and Trombetti7, Lemma 2.5], F is
![]() $(m^{2},k)$
-subnormal. The statement follows from [Reference Lennox9, Theorem A].
$(m^{2},k)$
-subnormal. The statement follows from [Reference Lennox9, Theorem A].
The last part of this section is devoted to our second main theorem concerning
![]() $\mathfrak {X}(m,k)$
-groups which contain a large abelian subgroup not necessarily normal.
$\mathfrak {X}(m,k)$
-groups which contain a large abelian subgroup not necessarily normal.
Lemma 2.11. Let G be an
![]() $\mathfrak {X}(m,k)$
-group. If G contains a large abelian subgroup, then the Baer radical of G is a finite-index subgroup.
$\mathfrak {X}(m,k)$
-group. If G contains a large abelian subgroup, then the Baer radical of G is a finite-index subgroup.
Proof. Let B be the Baer radical of G. By Corollary 2.3, B is a large nilpotent subgroup of G, so that the section
![]() $B/B{'}$
has cardinality
$B/B{'}$
has cardinality
![]() $\aleph $
. Hence,
$\aleph $
. Hence,
![]() $G/B{'}$
is an
$G/B{'}$
is an
![]() $\mathfrak {X}(m,k)$
-group and contains the large abelian normal subgroup
$\mathfrak {X}(m,k)$
-group and contains the large abelian normal subgroup
![]() $B/B{'}$
, so that, as a consequence of Theorem 2.10,
$B/B{'}$
, so that, as a consequence of Theorem 2.10,
By Hall’s theorem,
![]() $\lvert G/B{'}: Z_{2\mu (m^2+k)}(G/B{'})\rvert $
is finite so, with
$\lvert G/B{'}: Z_{2\mu (m^2+k)}(G/B{'})\rvert $
is finite so, with
![]() $Z/B' =Z_{2\mu (m^2+k)}(G/B{'})$
, also
$Z/B' =Z_{2\mu (m^2+k)}(G/B{'})$
, also
![]() $\lvert G:ZB\rvert $
is finite. Clearly,
$\lvert G:ZB\rvert $
is finite. Clearly,
![]() $ZB/B{'}$
is nilpotent by Fitting’s theorem, and so the nilpotency of the normal subgroup B of
$ZB/B{'}$
is nilpotent by Fitting’s theorem, and so the nilpotency of the normal subgroup B of
![]() $ZB$
ensures that
$ZB$
ensures that
![]() $ZB$
is a nilpotent normal subgroup of G. It follows that
$ZB$
is a nilpotent normal subgroup of G. It follows that
![]() $Z \leq B$
and the statement is proved.
$Z \leq B$
and the statement is proved.
Theorem 2.12. Let G be an
![]() $\mathfrak {X}(m,k)$
-group. If G contains a large abelian subgroup A, then G is finite-by-nilpotent and
$\mathfrak {X}(m,k)$
-group. If G contains a large abelian subgroup A, then G is finite-by-nilpotent and
![]() $\gamma _{\mu (m^2+k) }(G)$
is small.
$\gamma _{\mu (m^2+k) }(G)$
is small.
Proof. If B is the Baer radical of G, then B is a large and nilpotent subgroup of G by Corollary 2.3. Since
![]() $G/B$
is finite by Lemma 2.11, as a consequence of Lemma 2.9,
$G/B$
is finite by Lemma 2.11, as a consequence of Lemma 2.9,
![]() $\gamma _{\mu (m^2+k)}(G)$
is small.
$\gamma _{\mu (m^2+k)}(G)$
is small.
In addition, Lemma 2.11 ensures the existence of a finitely generated subgroup F such that
![]() $G=FB$
. By Corollary 2.5, F is f-subnormal in G, so that there exists an f-series of the form
$G=FB$
. By Corollary 2.5, F is f-subnormal in G, so that there exists an f-series of the form
where either
![]() $\lvert F_{i+1}: F_{i}\rvert $
is finite or
$\lvert F_{i+1}: F_{i}\rvert $
is finite or
![]() $F_{i}$
is normal in
$F_{i}$
is normal in
![]() $F_{i+1}$
, for each
$F_{i+1}$
, for each
![]() $i \in \{0, \ldots , n-1 \}$
.
$i \in \{0, \ldots , n-1 \}$
.
We will prove that G is finite-by-nilpotent by induction on the length n of the f-series above. If
![]() $n=1$
, since G is an uncountable group, F is normal in G. On the other hand, [Reference Casolo and Mainardis2, Theorem 1.1] tells us that F is also finite-by-nilpotent so we can find a positive integer r such that the G-invariant subgroup
$n=1$
, since G is an uncountable group, F is normal in G. On the other hand, [Reference Casolo and Mainardis2, Theorem 1.1] tells us that F is also finite-by-nilpotent so we can find a positive integer r such that the G-invariant subgroup
![]() $\gamma _{r}(F)$
is finite, and
$\gamma _{r}(F)$
is finite, and
is nilpotent by Fitting’s theorem.
Assume now that
![]() $n>1$
. Then
$n>1$
. Then
![]() $\lvert F_{n-1}{\,:\,}F_{n-1}\cap B\rvert $
is finite and
$\lvert F_{n-1}{\,:\,}F_{n-1}\cap B\rvert $
is finite and
![]() $B\cap F_{n-1}$
is contained in the Baer radical of
$B\cap F_{n-1}$
is contained in the Baer radical of
![]() $F_{n-1}$
, so we can apply the inductive hypothesis to
$F_{n-1}$
, so we can apply the inductive hypothesis to
![]() $F_{n-1}$
which has to be a finite-by-nilpotent group. It follows that there exists a finite characteristic subgroup M of
$F_{n-1}$
which has to be a finite-by-nilpotent group. It follows that there exists a finite characteristic subgroup M of
![]() $F_{n-1}$
such that
$F_{n-1}$
such that
![]() $F_{n-1}/M$
is nilpotent (see [Reference Casolo and Mainardis2, Lemma 2.9]). If
$F_{n-1}/M$
is nilpotent (see [Reference Casolo and Mainardis2, Lemma 2.9]). If
![]() $F_{n-1}$
is normal in G, also M is G-invariant and
$F_{n-1}$
is normal in G, also M is G-invariant and
is nilpotent by Fitting’s theorem. Assume that
![]() $\lvert G:F_{n-1}\rvert $
is finite; then M has finitely many conjugates in G, so that
$\lvert G:F_{n-1}\rvert $
is finite; then M has finitely many conjugates in G, so that
![]() $M^{G}$
is finite by Dietzmann’s lemma. On the other hand,
$M^{G}$
is finite by Dietzmann’s lemma. On the other hand,
is finite-by-(locally nilpotent) (see [Reference Casolo and Mainardis2, Lemma 2.7]), so that G itself is finite-by-(locally nilpotent), and hence actually finite-by-nilpotent by Corollary 2.2.