We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For a fixed integer e and prime p we construct the p-adic order bounded group valuations for a given abelian group G. These valuations give Hopf orders inside the group ring KG where K is an extension of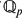 
with ramification index e. The orders are given explicitly when G is a p-group of order p or p 2. An example is given when G is not abelian.
