We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We define, for each quasisyntomic ring R (in the sense of Bhatt et al., Publ. Math. IHES 129 (2019), 199–310), a category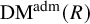 
$\mathrm {DM}^{\mathrm {adm}}(R)$ of admissible prismatic Dieudonné crystals over R and a functor from p-divisible groups over R to 
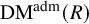$\mathrm {DM}^{\mathrm {adm}}(R)$. We prove that this functor is an antiequivalence. Our main cohomological tool is the prismatic formalism recently developed by Bhatt and Scholze.
