The axially symmetric deformation of a drop in a viscous fluid, under the influence of an externally imposed flow having simultaneous rotating and compressional or extensional components, is addressed. In the previous studies, two families of stationary drop shapes were constructed by simulating the dynamics of drop deformation: stable singly connected shapes with respect to axisymmetric disturbances, and unstable toroidal shapes. These two branches coexist at the same flow conditions, but were not connected. In this study, we obtain a new family of branches of unstable highly deformed stationary drops connecting with the stable flattened shapes and the toroidal ones. We use a method based on classical control theory. The controller is designed for a two-state dynamic model of the system and is employed on a high-order nonlinear dynamic model of the drop deformation. Through this feedback-control-centred approach, an extended collection of unstable stationary solutions is constructed, which spans the range from the loss of stability to the dimpled shapes almost collapsed at the centre. In the latter region, which was never obtained in previous studies, a multiplicity of solutions is identified.

Toroidal drops, embedded in viscous flow, have a large range of stationary shapes that are challenging to compute numerically due to their inherent instability. When both the drop and the outer fluid are Newtonian liquids, the only reported cases of such stable configurations are of highly expanded drops rotating in an axisymmetrical extensional flow. In this study, we propose a method for stabilizing the stationary shapes of inherently unstable rotating toroidal drops, embedded in extensional or biextensional flow, by subjecting the system to feedback control stabilization. The proposed controller is designed using a two-state dynamic model of the system and is tested on a high-order nonlinear dynamic model of the drop deformation. It is demonstrated that, through this simplified feedback-control-centred approach, an extended collection of stabilized stationary solutions is generated, which spans the range from highly expanded drops to almost collapsed ones. In the latter region, that was never obtained in previous studies, multiplicity of solutions is identified. Furthermore, our method is more accurate and more efficient compared with the previously used ones.

The deformation of an immiscible toroidal drop embedded in axisymmetric compressional Stokes flow is analysed via the boundary integral formulation in the case of equal viscosity. Numerical simulations are performed for the drop having initially the shape of a torus with circular cross-section. The quasi-stationary dynamic simulations reveal that, when the viscous forces, proportional to the intensity of the flow, are relatively weak compared with the surface tension (the ratio of these forces is characterized by the capillary number, $Ca$ ), three different scenarios of drop evolution are possible: indefinite expansion of the liquid torus, contraction to the centre and a stationary toroidal shape. When the intensity of the flow is low, the stationary shapes are shown to be close to circular tori. Once the outer flow strengthens, the cross-section of the stationary torus assumes first an elliptic and then an egg-like shape. For the capillary number greater than a critical value, $Ca_{cr}$ , toroidal stationary shapes were not found. Remarkably, $Ca_{cr}$ is close to the critical capillary number found previously for a simply connected drop flattened in compressional flow. Thus, a new example of non-uniqueness of stationary drop shape in viscous flow is obtained. Approximate stationary solutions in the form of tori with circular and elliptic cross-sections are obtained by minimizing the normal velocity over the drop interface. They are shown to be in good agreement with the stationary shapes from quasi-dynamic simulations for the corresponding intervals of the capillary number.

The dynamics of the deformation of a drop in axisymmetric compressional viscous flow is addressed through analytical and numerical analyses for a variety of capillary numbers, 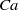$\mathit{Ca}$ , and viscosity ratios, 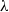$\lambda $ . For low 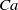$Ca$ , the drop is approximated by an oblate spheroid, and an analytical solution is obtained in terms of spheroidal harmonics; whereas, for the case of equal viscosities ( 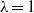$\lambda = 1$ ), the velocity field within and outside a drop of a given shape admits an integral representation, and steady shapes are found in the form of Chebyshev series. For arbitrary 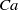$Ca$ and 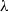$\lambda $ , exact steady shapes are evaluated numerically via an integral equation. The critical 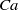$\mathit{Ca}$ , below which a steady drop shape exists, is established for various 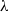$\lambda $ . Remarkably, in contrast to the extensional flow case, critical steady shapes, being flat discs with rounded rims, have similar degrees of deformation ( 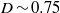$D\sim 0. 75$ ) for all 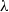$\lambda $ studied. It is also shown that for almost the entire range of 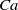$\mathit{Ca}$ and 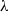$\lambda $ , the steady shapes have accurate two-parameter approximations. The validity and implications of spheroidal and two-parameter shape approximations are examined in comparison to the exact steady shapes.

We consider the deformation and breakup of a non-Newtonian slender drop in a Newtonian liquid, subject to an axisymmetric extensional flow, and the influence of inertia in the continuous phase. The non-Newtonian fluid inside the drop is described by the simple power-law model and the unsteady deformation of the drop is represented by a single partial differential equation. The steady-state problem is governed by four parameters: the capillary number; the viscosity ratio; the external Reynolds number; and the exponent characterizing the power-law model for the non-Newtonian drop. For Newtonian drops, as inertia increases, drop breakup is facilitated. However, for shear thinning drops, the influence of increasing inertia results first in preventing and then in facilitating drop breakup. Multiple stationary solutions were also found and a stability analysis has been performed in order to distinguish between stable and unstable stationary states.

A fluid-mechanical approach for the cleavage of biological cells is presented. The equations of motion were combined with concentration and orientation distribution balances, for active contractile filaments on the cell surface, to provide a dynamic evolution of interfacial forces and deformation. The resulting flow and the simultaneously developing surface-tension anisotropy provided a mechanism that facilitates the generation of a contractile ring at the cell equator: a major organelle in the establishment of cell furrow and the ultimate cleavage. The moving-boundary problem was solved numerically using boundary-integral representation for the Stokes equations which was modified to incorporate the anisotropic interfacial tensions.

Formal expressions are derived for the effective thermal conductivity Kij of randomly dispersed suspensions undergoing shear. These are then evaluated for the cases of dilute suspensions of cylinders and of spheres when the bulk motion is a simple shear, the Péclet number Pe is large, and the particle Reynolds number is small enough for inertia effects to be negligible. It is shown that as Pe → ∞ the presence of shear can significantly affect the O(ϕ) contribution to Kij (ϕ being the volume fraction of the solids), which becomes independent of k, the thermal conductivity of the suspended material. This results from the presence of regions of closed streamlines surrounding each particle which, for sufficiently large Pe, attain an isothermal state and therefore act as regions of infinite conductivity.

The Stokes equations describing the creeping motion of two arbitrary-sized touching spheres are solved exactly through the use of tangent-sphere coordinates. For the case of a linear shear field at infinity, explicit results covering the entire range of size ratios are presented for: (a) the forces and torques on the aggregate; (b) the hydrodynamic forces on the individual spheres comprising a freely suspended aggregate, which are in general non-zero; (c) the contribution of the pair to the bulk stress of a dilute suspension; and (d) under free suspension conditions, the velocity of any material point relative to that of the undisturbed flow.

An exact solution for the velocity field induced by the slow rolling motion of a sphere in contact with a permeable surface is derived. The porous solid and the viscous fluid each occupies a semi-infinite space.

It is shown that, by the use of conformal mapping, the problem is reduced to a fourth order ordinary linear boundary value problem. As the permeability of the porous body diminishes the important functionals, e.g. the force and torque resisting the rolling motion of the sphere, are divergent. The nature of this divergence is found and the dependence on the permeability of the porous solid is explicitly evaluated.