We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let A = (ank) and x = {sn} (n,k = 0,1,2, … ) be a matrix and a sequence of complex numbers, respectively. We write formally
(1.1)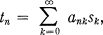
and say that the sequence x is summable A to the sum t or that the A matrix sums the sequence x to the value t if the series in (1.1) converges and
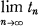
exists and equals t. We say that the matrix A is regular provided it sums every convergent sequence to its limit.
