Suppose that G is a finitely presented group, and that we are given a set of generators for a subgroup H of finite index in G. In this paper we describe an algorithm by which a set of defining relations may be found for H in these generators.

The algorithm is suitable for programming on a digital computer. It appears to have significant computational advantages over the method of Mendelsohn [8] (which is based on the Schreier-Reidemeister results, see for example [4, pp. 91–95]) in those cases where the generators of H are given as other than the familiar Schreier-Reidemeister generators.

1. Discussion of results

1·1. Introduction: The classical theorem of Lagrange states that the order of a subgroup of a finite group G divides the order, (G), of G. More generally, if H and K are subgroups of G, and H ≥ K, then (G:K) = (G:H)(H:K), where (G:K) denotes the index of K in G, etc. We call a number a possible order of a subgroup of G if it is a divisor of (G), and a possible order of a subgroup of G containing a subgroup H if it is a divisor of (G) and a multiple of (H). In this paper we discuss conditions on G for the existence of subgroups of every possible order, the existence of subgroups of every possible order containing arbitrary subgroups, and similar properties.

Following, for example, Kurošs [8], we define the (transfinite) upper central series of a group G to be the series

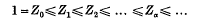
such that Zα + 1/Za is the centre of G/Zα, and if β is a limit ordinal, then 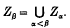If α is the least ordinal for which Zα =Zα+1=…, then we say that the upper central series has length α, and that Zα= His the hypercentre of G. As usual, we call G nilpotent if Zn= Gfor some finite n.

Let an element of a group be called an FC element if it has only a finite number of conjugates in the group. Baer(1) and Neumann (8) have discussed groups in which every element is FC, and called them FC-groups. Both Abelian and finite groups are trivially FC-groups; Neumann has studied the properties common to FC-groups and Abelian groups, and Baer the properties common to FC-groups and finite groups. Baer has also shown that, for an arbitrary group G, the set H1 of all FC elements is a characteristic subgroup. Haimo (3) has defined the FC-chain of a group G by

Hi/Hi−1 is the subgroup of all FC elements in G/Hi−1.

1. If P is any property of groups, then we say that a group G is ‘locally P’ if every finitely generated subgroup of G satisfies P. In this paper we shall be chiefly concerned with the case when P is the property of being nilpotent, and will examine some properties of nilpotent groups which also hold for locally nilpotent groups. Examples of locally nilpotent groups are the locally finite p-groups (groups such that every finite subset is contained in a finite group of order a power of the prime p); indeed, every periodic locally nilpotent group is the direct product of locally finite p-groups.

The object of this note is to give an example of an infinite locally finite p-group which has no proper characteristic subgroup except the unit group. (A group G is a locally finite p-group if every finite set of elements of G generates a subgroup of finite order equal to a power of the prime p.) It is known that an infinite locally finite p-group cannot be simple, for if it were it would satisfy the minimal condition for normal subgroups, and so have a non-trivial centre (see(1)). However our example shows that it can be characteristically-simple. Examples are known of locally finite p-groups with trivial centre ((2), (4)), and of locally finite p-groups coinciding with their commutator groups ((1), (5)). Since the centre and commutator subgroup of a group are characteristic subgroups our example will have both of these properties. We may remark that the direct product of a simple, or even of a characteristically-simple group with itself any number of times is also characteristically-simple, but by Corollary 2.1 our group cannot be so decomposed.