We discuss the 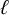 $\ell $-adic case of Mazur’s ‘Program B’ over
$\ell $-adic case of Mazur’s ‘Program B’ over  $\mathbb {Q}$: the problem of classifying the possible images of
$\mathbb {Q}$: the problem of classifying the possible images of 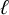 $\ell $-adic Galois representations attached to elliptic curves E over
$\ell $-adic Galois representations attached to elliptic curves E over  $\mathbb {Q}$, equivalently, classifying the rational points on the corresponding modular curves. The primes
$\mathbb {Q}$, equivalently, classifying the rational points on the corresponding modular curves. The primes 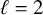 $\ell =2$ and
$\ell =2$ and  $\ell \ge 13$ are addressed by prior work, so we focus on the remaining primes
$\ell \ge 13$ are addressed by prior work, so we focus on the remaining primes 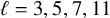 $\ell = 3, 5, 7, 11$. For each of these
$\ell = 3, 5, 7, 11$. For each of these 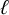 $\ell $, we compute the directed graph of arithmetically maximal
$\ell $, we compute the directed graph of arithmetically maximal 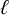 $\ell $-power level modular curves
$\ell $-power level modular curves 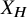 $X_H$, compute explicit equations for all but three of them and classify the rational points on all of them except
$X_H$, compute explicit equations for all but three of them and classify the rational points on all of them except 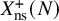 $X_{\mathrm {ns}}^{+}(N)$, for
$X_{\mathrm {ns}}^{+}(N)$, for 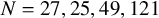 $N = 27, 25, 49, 121$ and two-level
$N = 27, 25, 49, 121$ and two-level 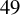 $49$ curves of genus
$49$ curves of genus 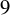 $9$ whose Jacobians have analytic rank
$9$ whose Jacobians have analytic rank 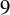 $9$.
$9$.
Aside from the 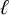 $\ell $-adic images that are known to arise for infinitely many
$\ell $-adic images that are known to arise for infinitely many  ${\overline {\mathbb {Q}}}$-isomorphism classes of elliptic curves
${\overline {\mathbb {Q}}}$-isomorphism classes of elliptic curves 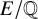 $E/\mathbb {Q}$, we find only 22 exceptional images that arise for any prime
$E/\mathbb {Q}$, we find only 22 exceptional images that arise for any prime 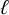 $\ell $ and any
$\ell $ and any 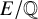 $E/\mathbb {Q}$ without complex multiplication; these exceptional images are realised by 20 non-CM rational j-invariants. We conjecture that this list of 22 exceptional images is complete and show that any counterexamples must arise from unexpected rational points on
$E/\mathbb {Q}$ without complex multiplication; these exceptional images are realised by 20 non-CM rational j-invariants. We conjecture that this list of 22 exceptional images is complete and show that any counterexamples must arise from unexpected rational points on 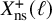 $X_{\mathrm {ns}}^+(\ell )$ with
$X_{\mathrm {ns}}^+(\ell )$ with 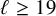 $\ell \ge 19$, or one of the six modular curves noted above. This yields a very efficient algorithm to compute the
$\ell \ge 19$, or one of the six modular curves noted above. This yields a very efficient algorithm to compute the 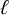 $\ell $-adic images of Galois for any elliptic curve over
$\ell $-adic images of Galois for any elliptic curve over  $\mathbb {Q}$.
$\mathbb {Q}$.
In an appendix with John Voight, we generalise Ribet’s observation that simple abelian varieties attached to newforms on 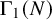 $\Gamma _1(N)$ are of
$\Gamma _1(N)$ are of 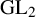 $\operatorname {GL}_2$-type; this extends Kolyvagin’s theorem that analytic rank zero implies algebraic rank zero to isogeny factors of the Jacobian of
$\operatorname {GL}_2$-type; this extends Kolyvagin’s theorem that analytic rank zero implies algebraic rank zero to isogeny factors of the Jacobian of 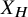 $X_H$.
$X_H$.
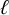 $\ell $-adic images of Galois for elliptic curves over
$\ell $-adic images of Galois for elliptic curves over  $\mathbb {Q}$ (and an appendix with John Voight)
$\mathbb {Q}$ (and an appendix with John Voight)
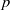 $p$-divisible groups, and random curves over finite fields
$p$-divisible groups, and random curves over finite fields