Recent studies focusing on the response of turbulent boundary layers (TBLs) to a step change in roughness have provided insight into the scaling and characterisation of TBLs and the development of the internal layer. Although various step-change combinations have been investigated, ranging from smooth-to-rough to rough-to-smooth, the minimum required roughness fetch length over which the TBL returns to its homogeneously rough behaviour remains unclear. Moreover, the relationship between a finite- and infinite-fetch roughness function (and the equivalent sand-grain roughness) is also unknown. In this study, we determine the minimum ‘equilibrium fetch length’ for a TBL developing over a smooth-to-rough step change as well as the expected error in local skin friction if the fetch length is under this minimum threshold. An experimental study is carried out where the flow is initially developed over a smooth wall, and then a step change is introduced using patches of P24 sandpaper. Twelve roughness fetch lengths are tested in this study, systematically increasing from 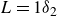$L = 1\delta _2$ up to 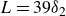$L = 39\delta _2$ (where L is the roughness fetch length and 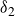$\delta _2$ is the TBL thickness of the longest fetch case), measured over a range of Reynolds numbers (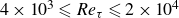$4\times 10^3 \leqslant Re_\tau \leqslant 2\times 10^4$). Results show that the minimum fetch length needed to achieve full equilibrium recovery is around 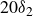$20\delta _2$. Furthermore, we observe that the local friction coefficient, 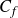$C_{\! f}$, recovers to within 10 % of its recovered value for fetch lengths 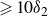$\geqslant 10\delta _2$. This information allows us to incorporate the effects of roughness fetch length on the skin friction and roughness function.

We examine the behaviour of turbulent boundary layers over surfaces composed of spanwise-alternating smooth and rough strips, where the width of the strips $S$ varies such that $0.32\leqslant S/\overline{\unicode[STIX]{x1D6FF}}\leqslant 6.81$, where $\overline{\unicode[STIX]{x1D6FF}}$ is the boundary-layer thickness averaged over one spanwise wavelength of the heterogeneity. The experiments are configured to examine the influences of spanwise variation in wall shear stress over a large $S/\overline{\unicode[STIX]{x1D6FF}}$ range. Hot-wire anemometry and particle image velocimetry (PIV) reveal that the half-wavelength $S/\overline{\unicode[STIX]{x1D6FF}}$ governs the diameter and strength of the resulting mean secondary flows and hence the observed isovels of the mean streamwise velocity. Three possible cases are observed: limiting cases (either $S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$ or $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$), where the secondary flows are confined near the wall or near the roughness change, and intermediate cases ($S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$), where the secondary flows are space filling and at their strongest. These secondary flows, however, exhibit a time-dependent behaviour which might be masked by time averaging. Further analysis of the energy spectrogram and fluctuating flow fields obtained from PIV show that the secondary flows meander in a similar manner to that of large-scale structures occurring naturally in turbulence over smooth walls. The meandering of the secondary flows is a function of $S/\overline{\unicode[STIX]{x1D6FF}}$ and is most prominent when $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$.