In this work, a systematic study is carried out concerning the dynamic behaviour of finite-size spheroidal particles in non-isothermal shear flows between parallel plates. The simulations rely on a hybrid method combining the lattice Boltzmann method with a finite-difference solver. Fluid–particle and heat–particle interactions are accounted for by using the immersed boundary method. The effect of particle Reynolds number (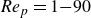$\textit{Re}_p=1{-}90$), Grashof number (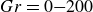${Gr}=0{-}200$), initial position and initial orientation of the particle are thoroughly examined. For the isothermal prolate particle, we observed that above a certain Reynolds number, the particle undergoes a pitchfork bifurcation; at an even higher Reynolds number, it returns to the centre position. In contrast, the hot particle behaves differently, with no pitchfork bifurcation. Instead, the Reynolds and Grashof numbers can induce oscillatory tumbling or log-rolling motions in either the lower or upper half of the channel. Heat transfer also plays an important role: at low Grashof numbers, the particle settles near the lower wall, while increasing the Grashof number shifts it towards the upper side. Moreover, the presence of thermal convection increases the rotational speed of the particle. Surprisingly, beyond the first critical Reynolds number, the equilibrium position of the thermal particle shifts closer to the centreline compared with that of a neutrally buoyant isothermal particle. Moreover, higher Grashof numbers can cause the particle to transition from tumbling to log-rolling or even a no-rotation mode. The initial orientation has a stronger influence at low Grashof numbers, while the initial position shows no strong effect in non-isothermal cases.