We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The boundary value problem
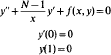
is studied with a view to obtaining the existence of positive solutions in C1([0, 1])∩C2((0, 1)). The function f is assumed to be singular in the second variable, with the singularity modeled after the special case f(x, y) = a(x)y−p, p>0.
This boundary value problem arises in the search of positive radially symmetric solutions to
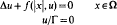
where Ω is the open unit ball in ℝN, centered at the origin, Γ is its boundary and |x| is the Euclidean norm of x.
The density u(x, t) of an ideal gas flowing through a homogeneous porous media satisfies the equation 
Here m > 1 is a physical constant and u also satisfies the initial condition 
If the initial data is not strictly positive it is necessary to work with generalized solutions of the Cauchy problem (1), (2) (see [1]). By a weak solution we shall mean a function u(x, t) such that for 
(in the sense of distributions) and 
