We explored the dynamics of Taylor–Couette flows within square enclosures, focusing primarily on the turbulence regime and vortex behaviour at varying Reynolds numbers. Laboratory experiments were conducted using particle image velocimetry for Reynolds numbers 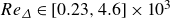$Re_{\varDelta }\in [0.23, 4.6]\times 10^3$ based on the minimum gap 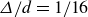$\varDelta /d = 1/16$, 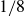$1/8$ and 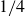$1/4$, where 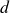$d$ is the cylinder diameter, or 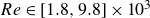$Re\in [1.8, 9.8]\times 10^3$ based on 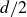$d/2$. At lower 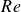$Re$, the flow was dominated by well-defined Taylor and Görtler vortices, while higher 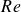$Re$ led to a turbulent state with distinct motions. Space–time radial velocity analysis revealed persistent Taylor vortices at lower 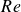$Re$, with larger gaps but increased turbulence, and irregular motions at higher 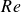$Re$, with smaller gaps. Velocity spectra reveal that the energy distribution is maintained at frequencies lower than the integral-type frequency 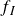$f_I$ across varying $\varDelta$ due to the dominance of large vortices. However, there is a monotonic increase in energy at higher frequencies beyond 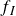$f_I$. The reduced characteristic frequency 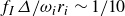$f_I\varDelta /\omega _ir_i \sim 1/10$ indicates that these motions scale linearly with angular velocity, and inversely with the gap. Proper orthogonal decomposition (POD) and spectral POD were used to distinguish between Taylor and Görtler vortices, showing the effects of gap size and the associated energy cascade. Linear stability analysis included as complementary support revealed primary instability of the Taylor vortex, which is similar to the circular enclosure, along with multiple corner modes that are unique to the geometry.