We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let U B(p 0; ρ 1) × f M V be a cylindrically bounded domain in a warped product manifold 
:= M B × f M V and let M be an isometrically immersed submanifold in . The purpose of this paper is to provide explicit radii of the geodesic balls of M which first exit from U B(p 0; ρ 1) × f M V for the case in which the mean curvature of M is sufficiently small and the lower bound of the Ricci curvature of M does not diverge to –∞ too rapidly at infinity.
Let M be an n-dimensional Hadamard manifold, that is, a complete simply connected C∞ Riemannian manifold with nonpositive sectional curvatures. Making use of geodesic rays, Eberlein and O’Neill [11] constructed a compactification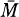 
= M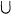
S(∞) of M which gives a homeomorphism of (M, S(∞)) with the Euclidean pair (Bn, Sn-1 ). In this paper we shall study the asymptotic Dirichlet problem for the Laplace-Beltrami operator, which is stated as follows:
