We prove a reverse Faber–Krahn inequality for the Cheeger constant, stating that every convex body in ℝ2 has an affine image such that the product between its Cheeger constant and the square root of its area is not larger than the same quantity for the regular triangle. An analogous result holds for centrally symmetric convex bodies with the regular triangle replaced by the square. We also prove a Mahler-type inequality for the Cheeger constant, stating that every axisymmetric convex body in ℝ2 has a linear image such that the product between its Cheeger constant and the Cheeger constant of its polar body is not larger than the same quantity for the square.

Motivated by a long-standing conjecture of Pólya and Szegö about the Newtonian capacityof convex bodies, we discuss the role of concavity inequalities in shape optimization, andwe provide several counterexamples to the Blaschke-concavity of variational functionals,including capacity. We then introduce a new algebraic structure on convex bodies, whichallows to obtain global concavity and indecomposability results, and we discuss theirapplication to isoperimetric-like inequalities. As a byproduct of this approach we alsoobtain a quantitative version of the Kneser-Süss inequality. Finally, for a large class offunctionals involving Dirichlet energies and the surface measure, we perform a localanalysis of strictly convex portions of the boundary via second ordershape derivatives. This allows in particular to exclude the presence of smooth regionswith positive Gauss curvature in an optimal shape for Pólya-Szegö problem.

Lower semicontinuity results are obtained for multipleintegrals of the kind $\int _{\mathbb{R}^n}\!f(x, \!\nabla_\mu u\!){\rm d} \mu$ 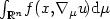,where μ is a given positive measure on $\mathbb{R}^n$ 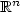, and thevector-valued function u belongs to the Sobolev space $H^{1,p}_\mu (\mathbb{R}^n, \mathbb{R}^m)$ 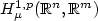associated with μ. The proofs areessentially based on blow-up techniques, and a significant role isplayed therein by the concepts of tangent space and of tangentmeasures to μ. More precisely, for fully general μ, anotion of quasiconvexity for f along the tangent bundle toμ, turns out to be necessary for lower semicontinuity; thesufficiency of such condition is also shown, when μ belongs toa suitable class of rectifiable measures.

We consider some definitions of tangent space to a Radon measure μ on ℝn that have been given in the literature. In particular, we focus our attention on a recent distributional notion of tangent vector field to a measure and we compare it to other definitions coming from ‘geometric measure theory’, based on the idea of blow-up. After showing some classes of examples, we prove an estimate from above for the dimension of the tangent spaces and a rectifiability theorem which also includes the case of measures supported on sets of variable dimension.