The formation of pressure-induced casein structures (600 MPa for 30 min at 30°C) was investigated for different pressure release rates (20 to 600 MPa min−1) and casein contents (1 to 15 g/100 ml). Structures from liquid (sol) to solid (gel) were observed. The higher the protein content and the pressure release rate, the higher was the dynamic viscosity. A firm gel was built up at a casein content of 7 g/100 ml for a pressure release rate of 600 MPa min−1, while lower release rates resulted in less firm gels (200 MPa min−1) or liquid structures (20 MPa min−1). In a 5 g/100 ml casein solution and at a pressure release rate of 600 MPa min−1, casein aggregates were generated which were built from smaller casein particles with a larger hydrodynamic diameter and higher voluminosity than in the untreated solution. After a slow release rate casein micelles had a smaller hydrodynamic diameter and a lower voluminosity, but were similar in shape and diameter as compared with the micelles in solution before high pressure treatment.

The thermal resistance of the lactococcal bacteriophage P008 was investigated between 55 and 80 °C. Inactivation kinetics revealed an order of reaction above 1 and could be determined by a non-1st-order regression model. Phage inactivation was influenced by the medium (milk and Ca-M17-broth). Within the investigated temperature range, milk had a protective effect on phage P008. This was reflected in the rate constant and in the activation energy. Thermal phage inactivation studies reported in literature were re-analysed using non-1st-order regression. The obtained kinetic parameters showed that phage P008 belongs to the most heat resistant lactococcal phages investigated so far.

Pressure processing of foodstuff has been applied to produce or modify proteinaceous gel structures. In real pressure processing the treatment is non-isothermal, due to the adiabatic nature of the process and the heat loss from the product to the vessel. In order to estimate the effect of pressurization on milk constituents pressure and temperature dependent kinetics were determined separately from each other. In a detailed kinetic study whey protein isolate was treated under isobaric (200 to 800 MPa) and isothermal conditions (−2 to 70 °C), and the resulting degree of denaturation of β-lactoglobulin A and B and α-lactalbumin was analysed. Kinetic parameters of denaturation were estimated using a one step non-linear regression method which allowed a global fit of the whole data set. The isobaric isothermal denaturation of β-lactoglobulin and α-lactalbumin was found to follow third and second order kinetics, respectively. Isothermal pressure denaturation of both β-lactoglobulin fractions do not differ significantly and were characterized by an activation volume decreasing with increasing temperature from −10 to about −30 ml mol−1, which demonstrates that the denaturation rate is accelerated with increasing temperature. The activation energy of about 70 to 100 kJ mol−1 obtained for β-lactoglobulin A and B is not dependent to a great extent on the pressure which indicates that above 200 MPa denaturation rate is limited by the aggregation rate while pressure forces unfolding of the molecule.

A Banach space X has the average distance property if there exists a unique real number r such that for each positive integer n and all x1,…,xn in the unit sphere of X there is some x in the unit sphere of X such that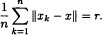

We show that lp does not have the average distance property if p > 2. This completes the study of the average distance property for lp spaces.