We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Linked-twist maps are area-preserving, piecewise diffeomorphisms, defined on a subset of the torus. They are non-uniformly hyperbolic generalizations of the well-known Arnold cat map. We show that a class of canonical examples have polynomial decay of correlations for 
$\alpha $-Hölder observables, of order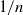 
$1/ n$.
