We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The propagation paths of oceanic internal tides are influenced by their interactions with vortices. We examine the scattering effect that an isolated vortex in (cyclo)geostrophic balance has on a rotating shallow-water plane wave. We run a suite of simulations in which we vary the non-dimensional vorticity of the vortex, 
$Ro$, the relative scale of the vortex size to the Rossby radius of deformation,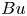 
$Bu$, and the size of the vortex compared with the plane wave wavelength, 
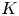$K$. We compare the scattered wave flux pattern with ray-tracing predictions. Ray-tracing predictions are relatively insensitive to 
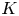$K$ in the 
$1< K<4$ range we investigate; however, they generally underestimate the broad angles of the shallow-water wave scattering patterns, especially for the lower end of the 
$K$ range. We then measure the ratio of the scattered wave energy flux to the incoming wave energy flux, denoted by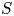 
$S$, for each simulation. We find that 
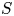$S$ follows a power law 
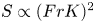$S \propto (FrK)^2$ when 
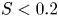$S < 0.2$, where 
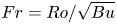$Fr = Ro/\sqrt {Bu}$ is the Froude number. When 
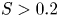$S>0.2$, it starts plateauing.
