In this paper we introduce Hardy-Lorentz spaces with variable exponents associated withdilations in ${{\mathbb{R}}^{n}}$ . We establish maximal characterizations and atomic decompositions for our variableexponent anisotropic Hardy-Lorentz spaces.

We establish that the maximal operator and the Littlewood–Paley g-function associated with the heat semigroup defined by multidimensional Bessel operators are of weak type (1, 1). We also prove that Riesz transforms in the multidimensional Bessel setting are of strong type (p, p), for every 1 < p < ∞, and of weak type (1, 1).

In this paper we establish that Hankel multipliers of Laplace transform type are bounded from 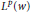${{L}^{p}}\left( w \right)$ into itself when 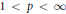$1\,<\,p\,<\infty$ , and from 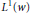${{L}^{1}}\left( w \right)$ into 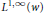${{L}^{1,\infty }}\left( w \right)$ , provided that $w$ is in the Muckenhoupt class 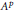${{A}^{p}}$ on 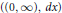$\left( \left( 0,\,\infty\right),\,dx \right)$ .

Riesz transforms $R_\mu$ related to the Bessel operators

$$\Delta_\mu=x^{-\mu-1/2}Dx^{2\mu+1}Dx^{-\mu-1/2}$$

are studied in this work. We develop for $R_\mu$ a theory that runs parallel to that for the Euclidean Hilbert transform. It is proved that $R_\mu$ is actually a Calderón–Zygmund singular integral operator. Also, $R_\mu$ is seen to be the boundary value of the appropriate harmonic extension for this context. Finally, we analyse weighted inequalities involving $R_\mu$.

In this paper we study Hankel transforms and Hankel convolution operators on spaces of entire functions of finite order and their duals.

In this paper we introduce the spaces of Hankel convolutors. We characterize the dual spaces of certain Hankel transformable function spaces as spaces of Hankel convolutors. Here the Hankel convolution and the Hankel transformation play an important role.