We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
1. Let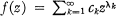 
be an analytic function with radius of convergence R (0 < R < ∞). Set
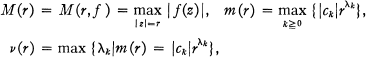
and let the order p and lower order ⋋ of f(z) be defined by
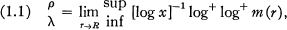
where x = Rr/(R — r). If 0 < ᑭ < ∞, we define the type T and lower type t of f(z) by
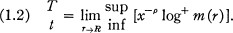
Also, if 0 < ᑭ < ∞, define the “growth numbers” 𝛄 and δ by
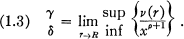
The purpose of our discussion will be to obtain some inequalities involving the growth constants defined above.
