We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Brun’s constant is the summation of the reciprocals of all twin primes, given by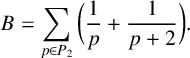 
$$ \begin{align*}B=\sum_{p \in P_2}{\bigg( \frac{1}{p} + \frac{1}{p+2}\bigg)}.\end{align*} $$
While rigorous unconditional bounds on B are known, we present the first rigorous bound on Brun’s constant under the assumption of GRH, yielding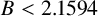 
$B < 2.1594$.
