We consider singular block operator problems of the type arising in the study of stability of the Ekman boundary layer. The essential spectrum is located, and an analysis of the $L^2$ solutions of a related first order system of differential equations allows the development of a Titchmarsh–Weyl coefficient $M(\lambda)$. This, in turn, permits a rigorous analysis of the convergence of approximations to the spectrum arising from regular problems. Numerical results illustrate the theory.

We prove some new results which justify the use of interval truncation as a means of regularising a singular fourth-order Sturm–Liouville problem near a singular endpoint. Of particular interest are the results in the so-called lim-3 case, which has no analogue in second-order singular problems.

This paper deals with the discrete groups of rigid motions of the hyperbolic plane. It is known (12) that the finitely generated, orientation-preserving groups have the following presentations:

Generators: .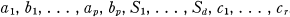

Defining relations: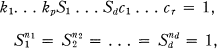

where km = ambmam-1bm-1 . We shall denote this group by F(p; n1 , … , nd; r).

In particular, the finitely generated free groups are contained among these. Indeed, one purpose of this paper is to indicate some geometrical methods for investigating free groups.