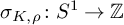This paper studies twisted signature invariants and twisted linking forms, with a view toward obstructions to knot concordance. Given a knot K and a representation $\rho $ of the knot group, we define a twisted signature function $\sigma _{K,\rho } \colon S^1 \to \mathbb {Z}$. This invariant satisfies many of the same algebraic properties as the classical Levine-Tristram signature 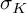$\sigma _K$. When the representation is abelian, $\sigma _{K,\rho }$ recovers 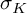$\sigma _K$, while for appropriate metabelian representations, 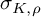$\sigma _{K,\rho }$ is closely related to the Casson-Gordon invariants. Additionally, we prove satellite formulas for 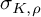$\sigma _{K,\rho }$ and for twisted Blanchfield forms.

This paper describes how to compute algorithmically certain twisted signature invariants of a knot $K$ using twisted Blanchfield forms. An illustration of the algorithm is implemented on $(2,q)$-torus knots. Additionally, using satellite formulas for these invariants, we also show how to obstruct the sliceness of certain iterated torus knots.

Given an L–space knot we show that its ϒ function is the Legendre transform of a counting function equivalent to the d–invariants of its large surgeries. The unknotting obstruction obtained for the ϒ function is, in the case of L–space knots, contained in the d–invariants of large surgeries. Generalisations apply for connected sums of L–space knots, which imply that the slice obstruction provided by ϒ on the subgroup of concordance generated by L–space knots is no finer than that provided by the d–invariants.

We apply the methods of Heegaard Floer homology to identify topological properties of complex curves in $\mathbb{C}P^{2}$. As one application, we resolve an open conjecture that constrains the Alexander polynomial of the link of the singular point of the curve in the case that there is exactly one singular point, having connected link, and the curve is of genus zero. Generalizations apply in the case of multiple singular points.

In [3] the authors (M. Borodzik and S. Friedl, Unknotting number and classical invariants (preprint 2012)) associated to a knot K ⊂ S3 an invariant nℝ(K), which is defined using the Blanchfield form and which gives a lower bound on the unknotting number. In this paper, we express nℝ(K) in terms of the Levine-Tristram signatures and nullities of K. We also show in the proof that the Blanchfield form for any knot K is diagonalisable over ℝ[t±1].