Performance-based managed entry agreements (PB-MEAs) might allow patient access to new medicines, but practical hurdles make competent authorities for pricing and reimbursement (CAPR) reluctant to implement PB-MEAs. We explored if the feasibility of PB-MEAs might improve by better aligning regulatory postauthorization requirements with the data generation of PB-MEAs and by active collaboration and data sharing. Reviewers from seven CAPRs provided structured assessments of the information available at the European Medicines Agency (EMA) Web site on regulatory postauthorization requirements for fifteen recently authorized products. The reviewers judged to what extent regulatory postauthorization studies could help implement PB-MEAs by addressing uncertainty gaps. Study domains assessed were: patient population, intervention, comparators, outcomes, time horizon, anticipated data quality, and anticipated robustness of analysis. Reviewers shared general comments about PB-MEAs for each product and on cooperation with other CAPRs. Reviewers rated regulatory postauthorization requirements at least partly helpful for most products and across domains except the comparator domain. One quarter of responses indicated that public information provided by the EMA was insufficient to support the implementation of PB-MEAs. Few PB-MEAs were in place for these products, but the potential for implementation of PB-MEAs or collaboration across CAPRs was seen as more favorable. Responses helped delineate a set of conditions where PB-MEAs may help reduce uncertainty. In conclusion, PB-MEAs are not a preferred option for CAPRs, but we identified conditions where PB-MEAs might be worth considering. The complexities of implementing PB-MEAs remain a hurdle, but collaboration across silos and more transparency on postauthorization studies could help overcome some barriers.

Glaciers located in western High Mountain Asia (HMA) have shown mass gain or limited mass losses compared to other mountain regions since ~2000. Increases in accumulation may be responsible. Although no contemporary measurements exist to explore this hypothesis, extensive historic measurements including firn density, stratigraphy and accumulation rates at ~4400 m a.s.l. on Abramov Glacier, Pamir Alay, provide valuable indications of accumulation changes. Abramov Glacier is located at the northern margin of western HMA. In this study, we assess unique historical firn data of Abramov Glacier from the 1970s to evaluate past firn conditions in this data sparse region. The current firn state is investigated based on a series of in situ measurements including firn cores and ground-penetrating radar measurements performed in 2018. We compare the legacy data with contemporary firn characteristics. Our results indicate a high year-to-year variability, but generally increasing net accumulation during the last 60 years on Abramov Glacier, with 0.84 ± 0.22 m w.e. for 2011–18 compared to 0.68 ± 0.32 m w.e. for 1965–72 and 0.59 ± 0.22 m w.e. for 1970–97. These results from in situ data provide ground truth for the data-sparse western HMA.

One crucial condition for the interpretation of ice-core records is the establishment of an accurate time-scale. This task is especially difficult for glacier sites in a complex topography such as the Alps, due to the often irregular deposition of fresh precipitation. In this work, dating techniques were applied to an Alpine ice core from upper Grenzgletscher, Monte Rosa massif (4200 m a.s.l.), representing about two-thirds of the total glacier thickness. They are based on (i) the radioactive decay of the isotope 210Pb, (ii) seasonally varying signals such as the concentrations of NH4 + and the isotopic ratio δ 18O, and (iii) stratigraphic markers from Saharan dust falls, atmospheric nuclear weapon tests and the reactor accident in Chernobyl. From the combined application of these dating methods, a time period of 1937–94 covered by the ice core was derived. Dating uncertainty is <1 year for the period 1970–94 and ± 2 years for the period 1937–69. The observed thinning of the annual layers as a function of depth could be well described by a simple kinematic glacier flow model.

This note points out a new aspect of the well-known relationship between the subjects mentioned in the title. The following result and its generalization in totally real algebraic number fields is central to the discussion. Let 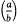denote the Legendre symbol for relatively prime numbers a and b ℇ ℤ and 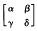a substitution of the modular subgroup Γ0(4). Then, if γ>0 and b≡1 mod 2,

with

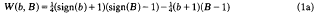
and

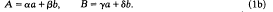
According to (1), the Legendre symbol behaves somewhat like a modular function ﹙apart from the known behaviour under 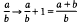and 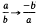﹚. (1) follows (see below) from the functional equation

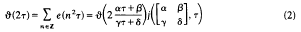
with

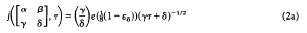
provided that

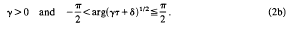
Here we used and always will use the abbreviation

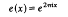
and ℇδ means the absolutely least residue of δ mod 4. In the proof, Hecke [4] assumed γ>0 (see also Shimura [5]).