Due to the increasing application of fractional calculus in engineering and biomedical processes, we analyze a new method for the numerical simulation of a large class of coupled systems of fractional-order partial differential equations. In this paper, we study shifted Jacobi polynomials in the case of two variables and develop some new operational matrices of fractional-order integrations as well as fractional-order differentiations. By the use of these operational matrices, we present a new and easy method for solving a generalized class of coupled systems of fractional-order partial differential equations subject to some initial conditions. We convert the system under consideration to a system of easily solvable algebraic equation without discretizing the system, and obtain a highly accurate solution. Also, the proposed method is compared with some other well-known differential transform methods. The proposed method is computer oriented. We use MatLab to perform the necessary calculation. The next two parts will appear soon.

For the $n$ -th order nonlinear differential equation, 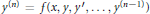${{y}^{(n)}}\,=\,f(x,\,y,\,y\prime ,\ldots ,\,{{y}^{(n-1)}})$ , we consider uniqueness implies uniqueness and existence results for solutions satisfying certain 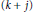$(k\,+\,j)$ -point boundary conditions for 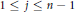$1\,\le \,j\,\le \,n\,-\,1$ and 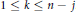$1\,\le \,k\,\le \,n\,-\,j$ . We define 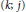$(k;\,j)$ -point unique solvability in analogy to $k$ -point disconjugacy and we show that 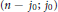$(n\,-\,{{j}_{0}};\,{{j}_{0}})$ -point unique solvability implies 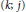$(k;\,j)$ -point unique solvability for 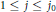$1\,\le \,j\,\le \,{{j}_{0}}$ , and 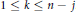$1\,\le \,k\,\le \,n\,-\,j$ . This result is analogous to $n$ -point disconjugacy implies $k$ -point disconjugacy for 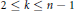$2\,\le \,k\,\le \,n\,-\,1$ .