Recent changes to US research funding are having far-reaching consequences that imperil the integrity of science and the provision of care to vulnerable populations. Resisting these changes, the BJPsych Portfolio reaffirms its commitment to publishing mental science and advancing psychiatric knowledge that improves the mental health of one and all.

Ruelle predicted that the maximal amplification of perturbations in homogeneous isotropic turbulence is exponential 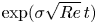$\exp ({\sigma \sqrt {Re} \,t})$ (where 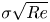$\sigma \sqrt {Re}$ is the maximal Lyapunov exponent). In our earlier works, we predicted that the maximal amplification of perturbations in fully developed turbulence is faster than exponential and is given by 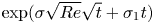$\exp ({\sigma \sqrt {Re} \sqrt {t} +\sigma _1 t})$ where 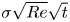$\sigma \sqrt {Re} \sqrt {t}$ is much larger than 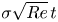$\sigma \sqrt {Re} \, t$ for small 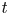$t$. That is, we predicted superfast initial amplification of perturbations. Built upon our earlier numerical verification of our prediction, here, we conduct a large numerical verification with resolution up to 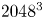$2048^3$ and Reynolds number up to 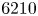$6210$. Our direct numerical simulation here confirms our analytical prediction. Our numerical simulation also demonstrates that such superfast amplification of perturbations leads to superfast nonlinear saturation. We conclude that such superfast amplification and superfast nonlinear saturation of ever existing perturbations suggest a mechanism for the generation, development and persistence of fully developed turbulence.