Alexandrov’s estimate states that if  $\Omega $ is a bounded open convex domain in
$\Omega $ is a bounded open convex domain in 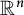 $\mathbb {R}^n$ and
$\mathbb {R}^n$ and  $u:\bar \Omega \to \mathbb {R}$ is a convex solution of the Monge-Ampère equation
$u:\bar \Omega \to \mathbb {R}$ is a convex solution of the Monge-Ampère equation 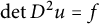 $\det D^2 u = f$ that vanishes on
$\det D^2 u = f$ that vanishes on  $\partial \Omega $, then
$\partial \Omega $, then 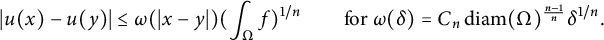 $$\begin{align*}|u(x) - u(y)| \le \omega(|x-y|)(\int_\Omega f)^{1/n} \qquad \text{for }\omega(\delta) = C_n\,\text{diam}(\Omega)^{\frac{n-1}n} \delta^{1/n}. \end{align*}$$
$$\begin{align*}|u(x) - u(y)| \le \omega(|x-y|)(\int_\Omega f)^{1/n} \qquad \text{for }\omega(\delta) = C_n\,\text{diam}(\Omega)^{\frac{n-1}n} \delta^{1/n}. \end{align*}$$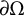 $\partial \Omega $. For example, we show that if the curvature is bounded away from
$\partial \Omega $. For example, we show that if the curvature is bounded away from 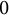 $0$, then the estimate remains valid if
$0$, then the estimate remains valid if 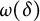 $\omega (\delta )$ is replaced by
$\omega (\delta )$ is replaced by 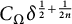 $C_\Omega \delta ^{\frac 12 + \frac 1{2n}}$. We determine the sharp constant
$C_\Omega \delta ^{\frac 12 + \frac 1{2n}}$. We determine the sharp constant 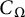 $C_\Omega $ when
$C_\Omega $ when 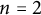 $n=2$, and when
$n=2$, and when 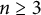 $n\ge 3$ and
$n\ge 3$ and 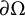 $\partial \Omega $ is
$\partial \Omega $ is 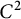 $C^2$, we determine the sharp asymptotics of the optimal modulus of continuity
$C^2$, we determine the sharp asymptotics of the optimal modulus of continuity 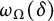 $\omega _\Omega (\delta )$ as
$\omega _\Omega (\delta )$ as 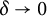 $\delta \to 0$. For arbitrary convex domains, we characterize the scaling of the optimal modulus
$\delta \to 0$. For arbitrary convex domains, we characterize the scaling of the optimal modulus 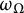 $\omega _\Omega $. Our results imply in particular that unless
$\omega _\Omega $. Our results imply in particular that unless 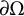 $\partial \Omega $ has a flat spot,
$\partial \Omega $ has a flat spot, 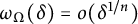 $\omega _\Omega (\delta ) = o(\delta ^{1/n})$ as
$\omega _\Omega (\delta ) = o(\delta ^{1/n})$ as 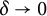 $\delta \to 0$, and under very mild nondegeneracy conditions, they yield the improved Hölder estimate,
$\delta \to 0$, and under very mild nondegeneracy conditions, they yield the improved Hölder estimate, 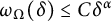 $\omega _\Omega (\delta ) \le C \delta ^\alpha $ for some
$\omega _\Omega (\delta ) \le C \delta ^\alpha $ for some 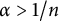 $\alpha>1/n$.
$\alpha>1/n$.