This paper deals with the problem of constructing multidimensional biorthogonal periodic multiwavelets from a given pair of biorthogonal periodic multiresolutions. Biorthogonal polyphase splines introduced to reduce the problem to a matrix extension problem, and an algorithm for solving the matrix extension problem is derived. Sufficient conditions for collections of periodic multiwavelets to form a pair of biorthogonal Riesz bases of the entire function space are also obtained.

This paper deals with Schauder decompositions of Banach spaces X2π of 2π-periodic functions by projection operators Pk onto the subspaces Vk, k = 0,1,…, which form a multiresolution of X2π,. The results unify the study of wavelet decompositions by orthogonal projections in the Hilbert space 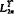on one hand and by interpolatory projections in the Banach space C2π on the other. The approach, using “orthogonal splines”, is constructive and leads to the construction of a Schauder decomposition of X2π and a biorthogonal system for X2π, and its dual X2π. Decomposition and reconstruction algorithms are derived from the construction.

Functionals of higher derivative type are linear combinations of functionals of the form f→f(n)(ζ), where n[ges ]2 and 0<[mid ]ζ[mid ]<1. The paper shows that, if L is a functional of higher derivative type and f is a function in the class S of univalent functions that maximises Re{L} over S, then L(f)≠0. In addition, if the function f is a rational function, then it must be a rotation of the Koebe function k(z)=z(1−z)−2. These results are applied to establish several cases of the two-functional conjecture for functionals of higher derivative type.