Let M be a von Neumann algebra, let 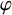 $\varphi $ be a normal faithful state on M and let
$\varphi $ be a normal faithful state on M and let 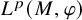 $L^p(M,\varphi )$ be the associated Haagerup noncommutative
$L^p(M,\varphi )$ be the associated Haagerup noncommutative 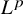 $L^p$-spaces, for
$L^p$-spaces, for 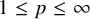 $1\leq p\leq \infty $. Let
$1\leq p\leq \infty $. Let 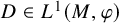 $D\in L^1(M,\varphi )$ be the density of
$D\in L^1(M,\varphi )$ be the density of 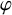 $\varphi $. Given a positive map
$\varphi $. Given a positive map 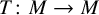 $T\colon M\to M$ such that
$T\colon M\to M$ such that 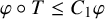 $\varphi \circ T\leq C_1\varphi $ for some
$\varphi \circ T\leq C_1\varphi $ for some 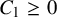 $C_1\geq 0$, we study the boundedness of the
$C_1\geq 0$, we study the boundedness of the 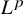 $L^p$-extension
$L^p$-extension 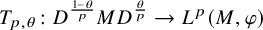 $T_{p,\theta }\colon D^{\frac {1-\theta }{p}} MD^{\frac {\theta }{p}}\to L^p(M,\varphi )$ which maps
$T_{p,\theta }\colon D^{\frac {1-\theta }{p}} MD^{\frac {\theta }{p}}\to L^p(M,\varphi )$ which maps 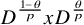 $D^{\frac {1-\theta }{p}} x D^{\frac {\theta }{p}}$ to
$D^{\frac {1-\theta }{p}} x D^{\frac {\theta }{p}}$ to 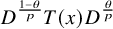 $D^{\frac {1-\theta }{p}} T(x) D^{\frac {\theta }{p}}$ for all
$D^{\frac {1-\theta }{p}} T(x) D^{\frac {\theta }{p}}$ for all 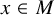 $x\in M$. Haagerup–Junge–Xu showed that
$x\in M$. Haagerup–Junge–Xu showed that 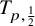 $T_{p,{\frac {1}{2}}}$ is always bounded and left open the question whether
$T_{p,{\frac {1}{2}}}$ is always bounded and left open the question whether 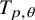 $T_{p,\theta }$ is bounded for
$T_{p,\theta }$ is bounded for 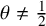 $\theta \not ={\frac {1}{2}}$. We show that for any
$\theta \not ={\frac {1}{2}}$. We show that for any 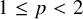 $1\leq p<2$ and any
$1\leq p<2$ and any 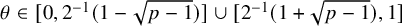 $\theta \in [0, 2^{-1}(1-\sqrt {p-1})]\cup [2^{-1}(1+\sqrt {p-1}), 1]$, there exists a completely positive T such that
$\theta \in [0, 2^{-1}(1-\sqrt {p-1})]\cup [2^{-1}(1+\sqrt {p-1}), 1]$, there exists a completely positive T such that 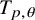 $T_{p,\theta }$ is unbounded. We also show that if T is
$T_{p,\theta }$ is unbounded. We also show that if T is 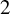 $2$-positive, then
$2$-positive, then 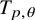 $T_{p,\theta }$ is bounded provided that
$T_{p,\theta }$ is bounded provided that 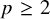 $p\geq 2$ or
$p\geq 2$ or 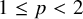 $1\leq p<2$ and
$1\leq p<2$ and 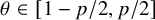 $\theta \in [1-p/2,p/2]$.
$\theta \in [1-p/2,p/2]$.
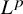 $L^p$-spaces
$L^p$-spaces
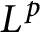 $L^p$-algebras
$L^p$-algebras