We present the dynamics of a hydrofoil free to oscillate in a plane as it interacts with vortices that are shed from a cylinder placed upstream. We consider cases where the cylinder is (i) fixed, (ii) forced to rotate constantly in one direction or (iii) forced to rotate periodically. When the upstream cylinder is fixed, at lower reduced velocities, the hydrofoil oscillates with a frequency equal to the frequency of vortices shed from the cylinder, and at higher reduced velocities with a frequency equal to half of the shedding frequency. When we force the cylinder to rotate in one direction, we control its wake and directly influence the response of the hydrofoil. When the rotation rate goes beyond a critical value, the vortex shedding in the cylinder's wake is suppressed and the hydrofoil is moved to one side and remains mainly static. When we force the cylinder to rotate periodically, we control the frequency of vortex shedding, which will be equal to the rotation frequency. Then at lower rotation frequencies, the hydrofoil interacts with one of the vortices in its oscillation path in the positive crossflow (transverse) direction, and with the second vortex in the negative crossflow direction, resulting in a 2:1 ratio between its inline and crossflow oscillations and a figure-eight trajectory. At higher rotation frequencies, the hydrofoil interacts with both shed vortices on its positive crossflow path and again in its negative crossflow path, resulting in a 1:1 ratio between its inline and crossflow oscillations and a linear trajectory.

We study flow-induced vibrations of a square prism free to oscillate in two degrees of freedom (cross-flow (CF) and inline (IL)), and placed in flow at varying angles of attack, by measuring the prism's displacement and flow-induced forces in both degrees of freedom experimentally, and conducting hydrogen bubble visualizations, as well as bubble image velocimetry. At large angles of attack (where 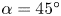$\alpha = 45^{\circ }$ corresponds to the case where one of the edges of the prism sees the flow first), we observe a two degree of freedom vortex-induced vibration (VIV) response with a figure-eight trajectory, similar to what has been observed for a cylinder with two degrees of freedom. As the angle of attack is decreased, the figure-eight trajectory transitions to a teardrop trajectory, suggesting a $1:1$ ratio between the oscillation frequencies in the CF and IL directions. The VIV response remains to be the dominant response down to an angle of attack of 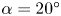$\alpha = 20^{\circ }$. At angles of attack of 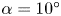$\alpha = 10^{\circ }$ and 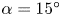$\alpha = 15^{\circ }$, the VIV response becomes negligible and elliptical trajectories are observed at higher reduced velocities. These elliptical trajectories then become four-lobe trajectories with amplitudes mainly in the CF direction at the lowest angles of attack (where a side of the square sees the flow first) and galloping-type response is observed, where the amplitude of oscillations is increased with increasing reduced velocity. Deviations from a typical galloping response are observed due to synchronizations between the shedding frequency and oscillation frequency at ranges of higher reduced velocities.