Let n = p 1 p 2 … pr be a product of r prime numbers which are not necessarily different. We define then an arithmetic function µm (n) by

where m is a natural number. We further define the function L(s, µm ) by the Dirichlet series

and will show that L(s, µm ), (m ≥ 3), has an infinitely many valued analytic continuation into the half plane Re s > ½.

We denote by (A) Artin’s reciprocity law for a general abelian extension of a finite degree over an algebraic number field of a finite degree, and denote two special cases of (A) as follows: by (AC) the assertion (A) where K/F is a cyclotomic extension; by (AK) the assertion (A) where K/F is a Kummer extension. We will show that (A) is derived from (AC) and (AK) only by routine, elementarily algebraic arguments provided that n = (K : F) is odd. If n is even, then some more advanced tools like Proposition 2 are necessary. This proposition is a consequence of Hasse’s norm theorem for a quadratic extension of an algebraic number field, but weaker than the latter.

The purpose of this paper is to characterize by means of simple quadratic forms the set of rational primes that are decomposed completely in a non-abelian central extension which is abelian over a quadratic field. More precisely, let L = Q be a bicyclic biquadratic field, and let K = Q. Denote by the ray class field mod m of K in narrow sense for a large rational integer m. Let be the maximal abelian extension over Q contained in and be the maximal extension contained in such that Gal(/L) is contained in the center of Gal(/Q). Then we shall show in Theorem 2.1 that any rational prime p not dividing d1d2m is decomposed completely in /Q if and only if p is representable by rational integers x and y such that x ≡ 1 and y ≡ 0 mod m as follows

where a, b, c are rational integers such that b 2 − 4ac is equal to the discriminant of K and (a) is a norm of a representative of the ray class group of K mod m.

Moreover is decomposed completely in if and only if .

In the present paper, we show that an infinite dimensional vector whose components are Fourier coefficients of an automorphic form is characterized as an infinite dimensional vector which is annihilated by an infinite matrix constructed by the values of a Bessel function. Results and methods are all simple and concrete.

Although the idea in the present paper is applicable to more general cases, our investigation will be restricted to the case of automorphic forms of weight 0, i.e., automorphic functions, with respect to SL(2, Z) on the upper half plane, in order to explain the main idea distinctly.

The Airy integral is a formula concerning the Fourier transform of a function like sin x3 or cos x3 , and is written, for instance in [2], as

for x ≧ 0.

The purpose of this paper is to get a certain explicit expression of automorphic factors, formulated rather differently than usual, of the classically well known theta function

(1)

Die vorliegènde Arbeit ist eine Zusammenfassung einiger Tatsachen und Formeln betreffs einer Transformationsgruppe, die diskontinuierlich auf dem dreidimensionalen euklidischen Halbraum operiert. Eine solche Gruppe, die zum erstenmal in [5] betrachtet wurde, heiße hier eine diskontinuierliche Gruppe Picardschen Typus. Die in dieser Arbeit angegebenen Resultate ergeben sich grundsätzlich aus der allgemeinen Theorie der algebraischen Gruppen sowie der symmetrischen Räume, und aus der entsprechenden Theorie der Eisensteinschen Reihen. ([1], [2], [4], [6], [7]).

The aim of this paper is to point out a number-theoretical property of a certain product of values taken by an abelian function at points of finite order of the abelian variety on which the abelian function is considered We use the theory of power residues and the theory of complex multiplication, and the result is somewhat similar to the so-called Stickelberger’s relation in the theory of Gauss sums. A related investigation was previously made by the author in a special case of elliptic curves [2].

Eisenstein führte in seiner Abhandlung [1] einen durchsichtigen, analytischen Beweis des Reziprozitätsgesetzes der Potenzreste im rationalen und Gaussschen Zahlkörper. Zur kurzen Fassung seiner Methode im rationalen Fall, seien m und n positive ganzrationale Zahlen und sei

.

Es gibt zwei verschiedene Arten von Summen, die gewöhnlich Gausssche Summen genannt werden. Die eine Summe wird von einer Zahl ω ≠ 0 eines algebraischen Zahlkörpers F bestimmt.

The aim of the present work is to determine the Galois group of the maximal abelian extension ΩA over an algebraic number field Ω of finite degree, which we fix once for all.

Let Z be a continuous character of the Galois group of ΩA/Ω. Then, by class field theory, the character Z is also regarded as a character of the idele group of Ω. We call such Z character of Ω. For our purpose, it suffices to determine the group Xl of the characters of Ω whose orders are powers of a prime number l.

Let Ω be an algebraic number field of finite degree, which we fix once for all, and let K be a cyclic extension over Ω such that the degree of K/Ω is a powerof a prime number l. It is obvious that the norm group NK/ΩeK of the unit group ek of K, being a subgroup of the unit group e of Ω contains the groupconsisting of all-th powersof ε∈e.

Unter einem bizyklischen biquadratischen Zahlkörper verstehen wir einen absolut abelschen Zahlkörper vierten Grades, der von zwei verschiedenen quadratischen Zahlkörpern zusammengesetzt wird. Wir behandeln im folgenden die Einheiten- und Idealklassengruppe dieses Körpers, indem wir die Ergebnisse von [6] und [7] weiterführen.

We shall prove in the present note a theorem on units of algebraic number fields, applying one of the strongest formulations, be Hasse [3], of Grunwald’s existence theorem.

Mit Hilfe der Dedekindschen ζ-Funktion erhält man bekanntlich Klassenzahlrelationen gewisser algebraischen Zahlkörper. Ais ein Spezialfall gilt der

Satz l.1) Es sei K ein bizyklischer biquadratischer Zahlkörper und seien k0, k1und k2die drei quadratischen Teilkörper von K. Ferner seien h, h0, h1und h2die Klassenzahlen von K, k0, k1bzw. k3. Dann besteht die Relation

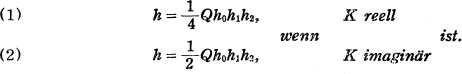
Hier ist Q der Index der Grupps der Einheiten 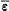, welche von der Einheiten von ki (i = 0, 1, 2) erzeugt wird, in der vollen Gruppe der Einheiten E von K: d.h. .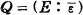