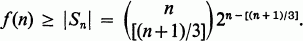Throughout this note, we adopt the graph-theoretical terminology and notation of Harary [3]. A graph G is hypohamiltonianif G is not hamiltonian but the deletion of any point u from G results in a hamiltonian graph G-u. Gaudin, Herz, and Rossi [2] proved that the smallest hypohamiltonian graph is the Petersen graph. Using a computer for a systematic search, Herz, Duby, and Vigué [4] found that there is no hypohamiltonian graph with 11 or 12 points. However, they found one with 13 and one with 15 points. Sousselier [4] and Lindgren [5] constructed independently the same sequence of hypohamiltonian graphs with 6k+10 points. Moreover, Sousselier found a cubic hypohamiltonian graph with 18 points. This graph and the Petersen graph were the only examples of cubic hypohamiltonian graphs until Bondy [1] constructed an infinite sequence of cubic hypohamiltonian graphs with 12k+10 points. Bondy also proved that the Coxeter graph [6], which is cubic with 28 points, is hypohamiltonian.

Let M(n) be the set of all the points (x 1, x 2,…, x n)∈E n such that x i∈{0,1,2} for each i= 1, 2,…, n and let f(n) be the cardinality of a largest subset of M(n) containing no three distinct collinear points. L. moser [4] asked for a proof of the inequality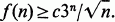

Let us consider the set Sn of those points (x 1x 2,…, x n)∈M(n) which satisfy |{i:X i= 1}| = [(n +1)/3]. As S n is a subset of the sphere with center at (1, 1,…, 1) and radius (n-[(n+1)/3])1/2, no three distinct points of S n are collinear. Thus we have

1

P. Erdös and G. Szekeres [1] proved that from any points in the plane one can always choose n + 1 of them which are the vertices of a convex polygon, thus answering a question due to Miss Esther Klein (who later became Mrs. G. Szekeres).

Call an m × n array an m × n; k array if its mn entries come from a set of k elements. An m × n; 1 array has mn like entries. We write

(1)

if every m × n; k array contains a p × q; 1 sub-array. The negation of (1) is written

and means that there is an m × n; k array containing no p × q; 1 sub-array. Relations (1) are called "polarized partition relations among cardinal numbers" by P. Erdös and R. Rado [2]. In this note we prove the following theorems.