We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the relationship between the reduction number of a primary ideal of a local ring relative to one of its minimal reductions and the multiplicity of the corresponding Sally module. This paper is focused on three goals: (i) to develop a change of rings technique for the Sally module of an ideal to allow extension of results from Cohen–Macaulay rings to more general rings; (ii) to use the fiber of the Sally modules of almost complete intersection ideals to connect its structure to the Cohen–Macaulayness of the special fiber ring; (iii) to extend some of the results of (i) to two-dimensional Buchsbaum rings. Along the way, we provide an explicit realization of the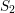 
$S_{2}$ -fication of arbitrary Buchsbaum rings.
