Suppose (R, m) is a local Noetherian domain with quotient field K and m-adic completion Ȓ. It is well known that the fibers of the morphism Spec(Ȓ) ₒ Spec(R), i.e., the formal fibers of R, encode important information about the structure of R. Perhaps the most important condition in Grothendieck’s definition of R being excellent is that the formal fibers of R be geometrically regular. Indeed, a local Noetherian ring is excellent provided it is universally catenary and has geometrically regular formal fibers [G, (7.8.3), page 214]. But the structure of the formal fibers of R is often difficult to determine. We are interested here in bringing out the interrelatedness of properties of the generic formal fiber of R with the existence of certain local Noetherian domains C birationally dominating R and having C/m C is a finite R-module.

Let D be a PID with infinitely many maximal ideals. J. W. Brewer has asked whether some simple ring extension D[α] of D must have nontrivial Picard group. We show that this question has a negative answer.

If R is an uncountable commutative ring, it is shown that there exists a proper subring of R having the same cardinality as R. It is also shown that if |R| = ω is an uncountable regular cardinal, and if R1 is a subring of R containing an identity of R and such that |R1| < ω, then there exists a proper R1 -subalgebra S of R such that |S| = |R|.

An integral domain D is said to be an essential domain if D is an intersection of valuation rings that are localizations of D. D is called a v-multiplication ring if the finite divisorial ideals of D form a group. Griffin has shown [2, pp. 717-718] that every v-multiplication ring is an essential domain, and that an essential domain having a defining family of valuation rings {Vα } which is of finite character (i.e., every nonzero element of D is a non-unit in at most finitely many Vα ) is necessarily a v-multiplication ring. It is noted in [4, p. 860] that any localization of a v-multiplication ring is again a v-multiplication ring. In this vein, Joe Mott has asked whether a localization of an essential domain must again be an essential domain. An example of an essential domain that is not a v-multiplication ring is given in [4], however it can be seen for this example that each localization is again an essential domain [6].

An integral domain D is called an essential ring if D = ∩αVα where the Vα are valuation rings which are quotient rings of D. D is called a v-multiplication ring if the finite divisorial ideals of D form a group. Griffin [2, pp. 717-718] has observed that every v-multiplication ring is essential and that an essential ring having a defining family of valuation rings {Vα} which is of finite character (i.e. every nonzero element of D is a non-unit in at most finitely many Vα) is necessarily a v-multiplication ring; but he conjectures that, in general, there exists an essential ring which is not a v-multiplication ring.

Throughout this paper R and D will denote integral domains with the same quotient field K. A set of integral domains {Di } i∊I with quotient field K will be said to have FC (“finite character” or “finiteness condition“) if 0 ≠ ξ ∊ K implies ξ is a unit of Di for all but finitely many i. If ∩i∊IDi also has quotient field K, then {Di } has FC if and only if every non-zero element in ∩i∊IDi is a non-unit in at most finitely many Di. A non-empty set {Vi}i∊:I of rank one valuation rings with quotient field K will be called a defining family of real R-representativesfor D if {V i} i∊:I has FC, R (⊄ ∩i∊I Vi, and D = R∩ (∩i∊I Vi).

If D is an integral domain with quotient field K, then by an overring of D we shall mean a ring D′ such that D ⊂ D′ ⊂ K. Gilmer and Ohm in [GO], Davis in [D] and Pendleton in [P] have studied the class of integral domains D having the property that each overring D′ of D is of the form Ds for some multiplicative system S of D. In [D] and [P] a domain with this property is called a Q-domain and in [GO] such a domain is said to have the QR-property. Slightly altering the terminology of [D] and [P], we shall say “QR-domain” instead of “Q-domain”. Noetherian QR-domains are precisely the Dedekind domains having torsion class group [GO; p. 97] or [D; p. 200]. Pendleton in [P; p. 500] classifies QR-domains as Prüfer domains satisfying the additional condition that the radical of each finitely generated ideal is the radical of a principal ideal. It is pointed out in [P; p. 500] that this characterization of QR-domains still leaves unresolved the question of whether the class group of a QR-domain is necessarily a torsion group. We show in §1 that a QR-domain need not have torsion class group. Our construction is direct; however, the problem can be viewed in terms of the realization of certain ordered abelian groups as divisibility groups of Prüfer domains, and we conclude §1 with a brief discussion of this approach to the problem.

This paper continues an investigation of the complete integral closure of an integral domain which was begun in [2]. We recall that if D is an integral domain with quotient field K then an element x of K is said to be almost integral over D if there exists a nonzero element y of D such that yxn is an element of D for each positive integer n. The set D* of elements of K almost integral over D is called the complete integral closure of D and D is said to be completely integrally closed if D* = D.

Let D be an integral domain with identity having quotient field K. A non-zero fractional ideal F of D is said to be divisorial if F is an intersection of principal fractional ideals of D[4; 2]. Equivalently, F is divisorial if there is a non-zero fractional ideal E of D such that

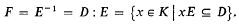
Divisorial ideals arose in the investigations of Van der Waerden, Artin, and Krull in the 1930's and were called v-ideals by Krull [9; 118]. The concept has played an important role in the development of multiplicative ideal theory.

Let A be an integral domain and K its quotient field. A is called a Krull domain if there is a set {V α} of rank one discrete valuation rings such that A = ∩α Vα and such that each non-zero element of A is a non-unit in only finitely many of the Vα. The structure of these rings was first investigated by Krull, who called them endliche discrete Hauptordungen (4 or 5, p. 104).

We consider in this paper only commutative rings with identity. When R is considered as a subring of S it will always be assumed that R and S have the same identity. If R is a subring of S an element s of S said to be integral over R if s is the root of a monic polynomial with coefficients in R. Following Krull [8], p. 102, we say s is almost integral over R provided all powers of s belong to a finite R-submodule of S. If R1 is the set of elements of S almost integral over R we say R1 is the complete integral closure of R in S.