We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Our main purpose in this paper is to propose the piecewise Legendre spectral-collocation method to solve Volterra integro-differential equations. We provide convergence analysis to show that the numerical errors in our method decay in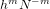 
$h^{m}N^{-m}$ -version rate. These results are better than the piecewise polynomial collocation method and the global Legendre spectral-collocation method. The provided numerical examples confirm these theoretical results.
