We treat the dielectric decrement induced by excess ion polarization as a source of ion specificity and explore its impact on electrokinetics. We employ a modified Poisson–Nernst–Planck (PNP) model accounting for the dielectric decrement. The dielectric decrement is determined by the excess-ion-polarization parameter  \alpha and when
\alpha and when  \alpha = 0 the standard PNP model is recovered. Our model shows that ions saturate at large zeta potentials
\alpha = 0 the standard PNP model is recovered. Our model shows that ions saturate at large zeta potentials 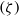 (\zeta ). Because of ion saturation, a condensed counterion layer forms adjacent to the charged surface, introducing a new length scale, the thickness of the condensed layer
(\zeta ). Because of ion saturation, a condensed counterion layer forms adjacent to the charged surface, introducing a new length scale, the thickness of the condensed layer 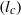 ({l}_{c} ). For the electro-osmotic mobility, the dielectric decrement weakens the electro-osmotic flow owing to the decrease of the dielectric permittivity. At large
({l}_{c} ). For the electro-osmotic mobility, the dielectric decrement weakens the electro-osmotic flow owing to the decrease of the dielectric permittivity. At large 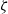 \zeta , when
\zeta , when 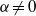 \alpha \not = 0, the electro-osmotic mobility is found to be proportional to
\alpha \not = 0, the electro-osmotic mobility is found to be proportional to 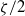 \zeta / 2, in contrast to
\zeta / 2, in contrast to 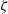 \zeta as predicted by the standard PNP model. This is attributed to ion saturation at large
\zeta as predicted by the standard PNP model. This is attributed to ion saturation at large 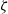 \zeta . In terms of the electrophoretic mobility
\zeta . In terms of the electrophoretic mobility  {M}_{e} , we carry out both an asymptotic analysis in the thin-double-layer limit and solve the full modified PNP model to compute
{M}_{e} , we carry out both an asymptotic analysis in the thin-double-layer limit and solve the full modified PNP model to compute 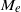 {M}_{e} . Our analysis reveals that the impact of the dielectric decrement is intriguing. At small and moderate
{M}_{e} . Our analysis reveals that the impact of the dielectric decrement is intriguing. At small and moderate 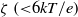 \zeta ~({\lt }6kT/ e), the dielectric decrement decreases
\zeta ~({\lt }6kT/ e), the dielectric decrement decreases 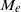 {M}_{e} with increasing
{M}_{e} with increasing  \alpha . At large
\alpha . At large 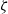 \zeta , it is known that the surface conduction becomes significant and plays an important role in determining
\zeta , it is known that the surface conduction becomes significant and plays an important role in determining 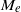 {M}_{e} . It is observed that the dielectric decrement effectively reduces the surface conduction. Hence in stark contrast,
{M}_{e} . It is observed that the dielectric decrement effectively reduces the surface conduction. Hence in stark contrast, 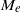 {M}_{e} increases as
{M}_{e} increases as  \alpha increases. Our predictions of the contrast dependence of the mobility on
\alpha increases. Our predictions of the contrast dependence of the mobility on  \alpha at different zeta potentials qualitatively agree with experimental results on the dependence of the mobility among ions and provide a possible explanation for such ion specificity. Finally, the comparisons between the thin-double-layer asymptotic analysis and the full simulations of the modified PNP model suggest that at large
\alpha at different zeta potentials qualitatively agree with experimental results on the dependence of the mobility among ions and provide a possible explanation for such ion specificity. Finally, the comparisons between the thin-double-layer asymptotic analysis and the full simulations of the modified PNP model suggest that at large 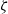 \zeta the validity of the thin-double-layer approximation is determined by
\zeta the validity of the thin-double-layer approximation is determined by  {l}_{c} rather than the traditional Debye length.
{l}_{c} rather than the traditional Debye length.