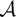Refine search
Actions for selected content:
7 results
GCR and CCR Steinberg Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1581-1606
- Print publication:
- December 2020
-
- Article
- Export citation
THE PRIME IDEALS AND SIMPLE MODULES OF THE UNIVERSAL ENVELOPING ALGEBRA U(𝔟⋉V2)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. S77-S98
- Print publication:
- December 2020
-
- Article
- Export citation
On a Theorem of Burgess and Stephenson
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 06 December 2018, pp. 603-605
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
MODULES OVER QUANTUM LAURENT POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 19 March 2012, pp. 323-341
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Combinatorial Gelfand models for some semigroups and q-rook monoid algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 707-718
-
- Article
-
- You have access
- Export citation
Semiclassical limits of quantum affine spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 387-407
-
- Article
-
- You have access
- Export citation
Classes of modules with many direct summands
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-19
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation