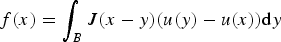Refine search
Actions for selected content:
6 results
SUMMABILITY AND ASYMPTOTICS OF POSITIVE SOLUTIONS OF AN EQUATION OF WOLFF TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 535-544
- Print publication:
- December 2024
-
- Article
- Export citation
Nonlocal problems in perforated domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 January 2019, pp. 305-340
- Print publication:
- February 2020
-
- Article
- Export citation
Kesten's bound for subexponential densities on the real line and its multi-dimensional analogues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 373-395
- Print publication:
- June 2018
-
- Article
- Export citation
Integrable Properties of a Variant of the Discrete Hungry Toda Equations and Their Relationship to Eigenpairs of Band Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 785-798
- Print publication:
- November 2017
-
- Article
- Export citation
Linear non-local diffusion problems in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 833-863
- Print publication:
- August 2016
-
- Article
- Export citation
Asymptotic Behaviour of the Time-Fractional Telegraph Equation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 890-893
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation