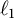Refine search
Actions for selected content:
5 results
On the complete separation of unique
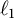 $\ell _{1}$ spreading models and the Lebesgue property of Banach spaces
$\ell _{1}$ spreading models and the Lebesgue property of Banach spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HANKEL MEASURES FOR FOCK SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 290-295
- Print publication:
- April 2023
-
- Article
- Export citation
A TRANSLATION THEOREM FOR THE GENERALISED ANALYTIC FEYNMAN INTEGRAL ASSOCIATED WITH GAUSSIAN PATHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 09 September 2015, pp. 152-161
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
ON PERIODIC SOLUTIONS FOR FIRST-ORDER DIFFERENTIAL EQUATIONS INVOLVING THE DISTRIBUTIONAL HENSTOCK–KURZWEIL INTEGRAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 06 February 2012, pp. 327-338
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
The Darboux problem involving the distributional Henstock–Kurzweil integral
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 197-205
-
- Article
-
- You have access
- Export citation