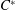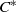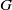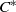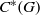Refine search
Actions for selected content:
6 results
Elements of
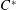 $C^{\ast }$-algebras Attaining their Norm in a Finite-dimensional Representation
$C^{\ast }$-algebras Attaining their Norm in a Finite-dimensional Representation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 93-111
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
An alternative axiomatic characterisation of pricing operators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1257-1264
- Print publication:
- December 2016
-
- Article
- Export citation
POLISH MODELS AND SOFIC ENTROPY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 18 January 2016, pp. 241-275
- Print publication:
- April 2018
-
- Article
- Export citation
LEBESGUE DECOMPOSITION FOR REPRESENTABLE FUNCTIONALS ON *-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 491-501
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
GROUPOID
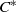 ${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 232-242
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
On a representation of continuous Volterra right inverses to the derivative in the spaces of infinitely differentiable functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-142
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation