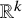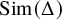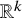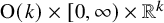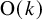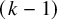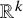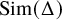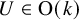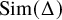Refine search
Actions for selected content:
4 results
Families of similar simplices inscribed in most smoothly embedded spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPLITTING LOOPS AND NECKLACES: VARIANTS OF THE SQUARE PEG PROBLEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e5
-
- Article
-
- You have access
- Open access
- Export citation
EXTREMAL PERIMETERS OF QUADRANGLES IN THE PONCELET PORISM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 13 February 2015, pp. 487-501
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
The bisectrix of a tetrahedron
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-103
- Print publication:
- June 1992
-
- Article
- Export citation