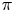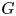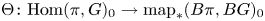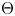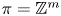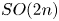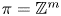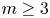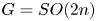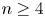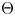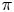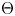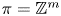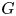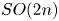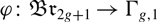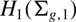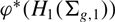Refine search
Actions for selected content:
3 results
The space of commuting elements in a Lie group and maps between classifying spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 735-755
- Print publication:
- June 2025
-
- Article
- Export citation
Braid groups, mapping class groups and their homology with twisted coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 249-266
- Print publication:
- March 2022
-
- Article
- Export citation
Anosov diffeomorphisms of products I. Negative curvature and rational homology spheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 553-569
- Print publication:
- February 2021
-
- Article
- Export citation