We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study computably enumerable equivalence relations (ceers), under thereducibility 
$R \le S$ if there exists a computable function f suchthat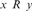 
$x\,R\,y$ if and only if 
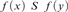$f\left( x \right)\,\,S\,f\left( y \right)$, for every 
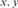$x,y$. We show that the degrees of ceers under the equivalencerelation generated by 
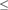$\le$ form a bounded poset that is neither a lower semilattice, noran upper semilattice, and its first-order theory is undecidable. We then studythe universal ceers. We show that 1) the uniformly effectively inseparable ceersare universal, but there are effectively inseparable ceers that are notuniversal; 2) a ceer R is universal if and only if 
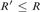$R\prime \le R$, where 
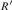$R\prime$ denotes the halting jump operator introduced by Gao and Gerdes(answering an open question of Gao and Gerdes); and 3) both the index set of theuniversal ceers and the index set of the uniformly effectively inseparable ceersare 
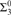${\rm{\Sigma }}_3^0$-complete (the former answering an open question of Gao andGerdes).
