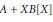Refine search
Actions for selected content:
3 results
The transcendence degree of an integral domain over a subfield and the dimension of the domain
-
- Journal:
- Nagoya Mathematical Journal / Volume 170 / 2003
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-162
-
- Article
-
- You have access
- Export citation
Examples of Half-Factorial Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 362-367
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation
On Complete Intersections and Their Hilbert Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 4 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-535
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation