Let 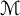 $\mathcal {M}$ be a semifinite von Nemann algebra equipped with an increasing filtration
$\mathcal {M}$ be a semifinite von Nemann algebra equipped with an increasing filtration 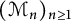 $(\mathcal {M}_n)_{n\geq 1}$ of (semifinite) von Neumann subalgebras of
$(\mathcal {M}_n)_{n\geq 1}$ of (semifinite) von Neumann subalgebras of 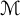 $\mathcal {M}$. For
$\mathcal {M}$. For 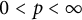 $0<p <\infty $, let
$0<p <\infty $, let 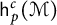 $\mathsf {h}_p^c(\mathcal {M})$ denote the noncommutative column conditioned martingale Hardy space and
$\mathsf {h}_p^c(\mathcal {M})$ denote the noncommutative column conditioned martingale Hardy space and 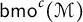 $\mathsf {bmo}^c(\mathcal {M})$ denote the column “little” martingale BMO space associated with the filtration
$\mathsf {bmo}^c(\mathcal {M})$ denote the column “little” martingale BMO space associated with the filtration 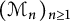 $(\mathcal {M}_n)_{n\geq 1}$.
$(\mathcal {M}_n)_{n\geq 1}$.
We prove the following real interpolation identity: if 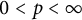 $0<p <\infty $ and
$0<p <\infty $ and 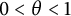 $0<\theta <1$, then for
$0<\theta <1$, then for 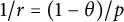 $1/r=(1-\theta )/p$,
$1/r=(1-\theta )/p$, 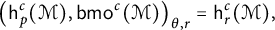 $$ \begin{align*} \big(\mathsf{h}_p^c(\mathcal{M}), \mathsf{bmo}^c(\mathcal{M})\big)_{\theta, r}=\mathsf{h}_{r}^c(\mathcal{M}), \end{align*} $$
$$ \begin{align*} \big(\mathsf{h}_p^c(\mathcal{M}), \mathsf{bmo}^c(\mathcal{M})\big)_{\theta, r}=\mathsf{h}_{r}^c(\mathcal{M}), \end{align*} $$
For the case of complex interpolation, we obtain that if 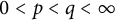 $0<p<q<\infty $ and
$0<p<q<\infty $ and 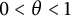 $0<\theta <1$, then for
$0<\theta <1$, then for 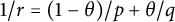 $1/r =(1-\theta )/p +\theta /q$,
$1/r =(1-\theta )/p +\theta /q$, 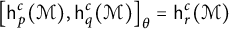 $$ \begin{align*} \big[\mathsf{h}_p^c(\mathcal{M}), \mathsf{h}_q^c(\mathcal{M})\big]_{\theta}=\mathsf{h}_{r}^c(\mathcal{M}) \end{align*} $$
$$ \begin{align*} \big[\mathsf{h}_p^c(\mathcal{M}), \mathsf{h}_q^c(\mathcal{M})\big]_{\theta}=\mathsf{h}_{r}^c(\mathcal{M}) \end{align*} $$
These extend previously known results from 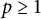 $p\geq 1$ to the full range
$p\geq 1$ to the full range 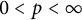 $0<p<\infty $. Other related spaces such as spaces of adapted sequences and Junge’s noncommutative conditioned
$0<p<\infty $. Other related spaces such as spaces of adapted sequences and Junge’s noncommutative conditioned 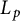 $L_p$-spaces are also shown to form interpolation scale for the full range
$L_p$-spaces are also shown to form interpolation scale for the full range 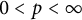 $0<p<\infty $ when either the real method or the complex method is used. Our method of proof is based on a new algebraic atomic decomposition for Orlicz space version of Junge’s noncommutative conditioned
$0<p<\infty $ when either the real method or the complex method is used. Our method of proof is based on a new algebraic atomic decomposition for Orlicz space version of Junge’s noncommutative conditioned 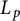 $L_p$-spaces.
$L_p$-spaces.
We apply these results to derive various inequalities for martingales in noncommutative symmetric quasi-Banach spaces.
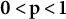 $\textbf {0<p<1}$
$\textbf {0<p<1}$