We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove almost everywhere convergence of continuous-time quadratic averages with respect to two commuting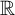 
$\mathbb {R}$-actions, coming from a single jointly measurable measure-preserving 
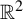$\mathbb {R}^2$-action on a probability space. The key ingredient of the proof comes from recent work on multilinear singular integrals; more specifically, from the study of a curved model for the triangular Hilbert transform.
