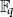Refine search
Actions for selected content:
6 results
A division algorithm for the Gaussian integers’ minimal Euclidean function
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1-14
-
- Article
- Export citation
PRODUCTION OPTIMIZATION FOR AGENTS OF DIFFERING WORK RATES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 24 September 2024, pp. 98-120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE EUCLIDEAN ALGORITHM: RHYTHM WITHOUT RECURSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 361-367
- Print publication:
- June 2023
-
- Article
- Export citation
1 - Euclidean Arithmetic
-
- Book:
- Algebraic Number Theory for Beginners
- Published online:
- 28 July 2022
- Print publication:
- 11 August 2022, pp 1-32
-
- Chapter
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation
Block Factorization of Hankel Matrices and EuclideanAlgorithm
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 5 / Issue 7 / 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 48-54
- Print publication:
- 2010
-
- Article
- Export citation